WTW 164

Unit 2.8: Volume of a solid of

revolution
Dr HR (Maya) Thackeray
<maya.thackeray@up.ac.za>
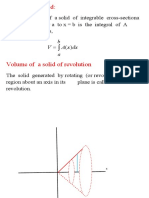
Volume of a solid of revolution
Let f be a continuous function on [a,b] with f(x) at least 0 for x in [a,b]. Let the area
between y = 0, y = f(x), x = a, and x = b be rotated about the x axis. The volume of the
solid we obtain is
.
That volume can be approximated by a collection of circular discs. The volume ΔV of
each disc is πy2 Δx.
Let f be a continuous function on [c,d] with f(y) at least 0 for y in [c,d]. Let the area
between x = 0, x = f(y), y = c, and y = d be rotated about the y axis. The volume of the
solid we obtain is
.
That volume can be approximated by a collection of circular discs. The volume ΔV of
each disc is πx2 Δy.
Questions (page 1)
• Find the volume of the solid obtained by revolving the area between y
= x2, y = 0, x = 0, and x = 1 about the x axis.
Solution.
Volume = = = = – 0 = .
Questions (page 2)
• Find the volume of the solid obtained by rotating the area between y
= ln x, y = 1, y = 2, and x = 0 about the y axis.
Solution. (We write exp x for e to the power of x.)
Volume = = = = (e4 – e2).
Questions (page 3)
• Find the volume of the solid obtained by revolving the area between y
= x2, y = 0, x = 0, and x = 1 about the y axis.
Solution.
Volume = π – π = π(1)2(1) – π = π – π
= π – π(1/2 – 0) = π/2.
Gabriel’s horn / Torricelli’s trumpet
Gabriel’s horn, also called Torricelli’s trumpet, is obtained by rotating
the curve y = 1/x for x 1 around the x axis. The volume of the solid is
= = = = π.
It is a tutorial exercise in unit 2.10 to show that the surface area of the
solid is infinite.