Machine Design II Prof. K.Gopinath & Prof. M.M.

Mayuram










Indian Institute of Technology Madras
Module 2 - GEARS
Lecture 4: WORKED OUT PROBLEMS ON INVOLUTE SPUR GEARS


Content

4.1 Introduction
4.2 Gear Calculation -Worked example 1
4.3 Gear Calculation -Worked example 2

4.1 INTRODUCTION

In the earlier lectures, the definition of gear, gear terminology, interference, methods of
eliminating interference, standard tooth systems for spur gears, profile shifted gears,
involutometry and design of gear blanks were dealt in detail. With the background of the
above knowledge, solving of simple gear problems will be dealt in this lecture.

4.2 GEAR CALCULATION Worked out example 1

In a drive, a velocity ratio of 2.5 with a centre distance of 70 mm is desired. (a) Determine
the pitch diameter of the gears with 20
o
full depth involute teeth; (b) Is there any
interference in the system? If so, how will you avoid it? (c) Determine the contact ratio, (d)
Find the dedendum, addendum, root diameters and the tip clearance, (e) If the centre
distance is increased by 1.5%, what will be the new pressure angle?

Given Data: i = 2.5; C = 70 mm; = 20
o
;
It is an involute full depth tooth system ;
To be found: m = ?; Z
1
= ? ; d
1
= ?; Interference exists or not ?;
Z
2
= ?; d
2
= ?; CR = ?
- We know that,
C = (r
1
+r
2
) = 0.5 m ( Z
1
+ Z
2
) = 0.5 m (Z
1
+ i Z
1
) = 70 mm
1
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram










Indian Institute of Technology Madras
From the above, i.e., m x Z
1
= 40
Possible solutions for standard modules as can be seen from the table:

Solution I:
m = 2mm, Z
1
= 20, Z
2
= i. Z
1
= 2.5 x 20 = 50
d
1
= m Z
1
= 2 x 20 = 40 mm
d
2
=i d
1
= 2.5 x 40 = 100 mm

STANDARD MODULES IN mm:
0.3 0.4 0.5 0.6 0.7 0.8 1.0
1.25 1.5 1.75 2.0 2.25 2.5 3.0
3.5 4.0 4.5 5.0 5.5 6.0 6.5
7 8 9 10 11 12 13
14 15 16 18 20 22 24
26 28 30 33 36 39 42
45 50 Further increase is in terms of 5 mm

Minimum number of teeth that can engage with the gear of 50 teeth without
interference is given by,

2 2
1 1 2 2
4k(z +k)
z + 2 z z =
sin
For full depth gears, k = 1. Substituting the values Z
2
= 50, = 20
o
in the above
equation,
+
+ =
2
1 1 2 o
4 x1( 50 1)
z 2 z x50
sin 20


=
2
z + 100 z 1744 0
1 1
i.e., Z
1min
= 15 is the minimum permissible number of teeth without interference.
Since from the above it is seen that, Z
1
> Z
1min
no interference will occur.

2
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram










Indian Institute of Technology Madras

















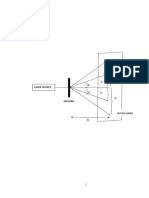
Fig 4.1. Path of Contact

Contact ratio, CR:
Referring to fig. 4.1, the path of contact:

L
a
= u
a
+ u
r


2 2 2 2 2 2
1 1 2 2 1 2
= + + + + L ( r a) r cos ( r a) r cos ( r r ) sin
a
| | |

Substituting the values,

= + + + +
=
o o
L ( ) cos ( ) cos ( ) sin
a
. mm
2 2 2 2 2 2
20 2 20 20 50 2 50 20 20 50 20
9798
o



3
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram










Indian Institute of Technology Madras
Now CR can be calculated with the formulae below,


= = = = =
L L
. .
a a
CR .
o
pcos m cos .
x x cos
| t |
t
9 798 9 798
1 660
5 901
2 20




For full depth tooth, the various values calculated are as shown below:

Addendum: a = 1m = 1x2 = 2mm

Dedendum: b = 1.25m = 1.25x2 = 2.5 mm

Clearance: c = 0.25 m = 0.25x2 = 0.5 mm

Pinion root circle diameter: d
r1
= d
1
- 2b = 40 2x2.5 = 35 mm

Pinion addendum diameter: d
a1
= d
1
+ 2a = 40 + 2x2 = 44 mm

Gear root circle diameter: d
r2
= d
2
- 2b = 100 2x2.5 = 95 mm

Gear addendum diameter: d
a2
= d
2
+ 2a = 100 + 2x2 = 104 mm


Solution II:

- The centre distance is given by, C = (r
1
+r
2
) = 0.5 m ( Z
1
+ Z
2
) = 0.5 m (Z
1
+ i Z
1
)
= 70 mm
Simplifying, m x Z
1
= 40
Another possible solution for standard module from the table is,
m = 2.5 mm, Z
1
= 16, Z
2
= i x Z
1
= 40,
d
1
= m Z
1
= 2.5x16=40 mm,
d
2
= m Z
2
= 2.5 x 40 =100 mm
Minimum number of teeth that can engage the gear of 40 teeth without interference
is given by,


2 2
1 1 2 2
4 k (z +k)
z + 2 z z =
sin

4
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram










Indian Institute of Technology Madras
For full depth gears k = 1. Substituting Z
2
= 40, = 20
o
, in the above equation,

4(40+ )
2
z + z x =
1 1 2 o
sin
1
2 40
20

=
2
z + 80 z 1402 0
1 1


i.e., Z
1min
= 15 is the minimum permissible without interference.

Since Z
1
> Z
1min
, no interference will occur.


Contact ratio, CR :
Referring to the fig. 4.1, the path of contact is given by,
L
a
= u
a
+ u
r


2 2 2 2 2 2
1 1 2 2 1 2
= + + + + L ( r a) r cos ( r a) r cos ( r r ) sin
a
| | |

Substituting the values,

= + + + +
=
2 2 2 o 2 2 2 o o
L ( 20 2.5 ) 20 cos 20 ( 50 2.5 ) 50 cos 20 ( 20 50 ) sin20
a
11.854 mm

Now CR can be calculated as,

= = = = =
11 854 11 854
1 607
5 901
2 5 20
L L
. .
a a
CR .
o
pcos m cos .
x . x cos
| t |
t

For full depth tooth the values are,
Addendum : a =1m = 1x2.5 =2.5mm

Dedendum : b =1.25m =1.25x2.5 = 3.125 mm

5
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram










Indian Institute of Technology Madras
Clearance: c = 0.25 m = 0.25x2.5 = 0.625 mm
[Pinion root circle diameter: d
r1
= d
1
- 2b = 40 2x3.125 = 33.75 mm
Pinion addendum diameter: d
a1
= d
1
+ 2a = 40+2x2.5 = 45 mm
Gear root circle diameter: d
r2
= d
2
- 2b = 100 2x3.125 = 93.75 mm
Pinion addendum diameter: d
a2
= d
2
+ 2a = 100 + 2x2.5 = 105 mm

New Pressure angle when the centre distance C is increased by 1.5% is given by:
= cos
-1
( r
1
cos20
o
/ r
1
1.015) = 22.21
o


4.3 GEAR CALCULATIONS- Worked out example 2

A 21 teeth gear has 20
o
full depth involute teeth with a module of 12mm. (a) Calculate the
radii of pitch circle, base circle and addendum circle (b) Determine the tooth thickness at
base circle, pitch circle and addendum circle. Comment on the top land thickness.
















=
b
r
r
cos|
= inv tan | | |
= +
t
1
t 2 r ( inv inv
2 r
1
) |

Fig 4.2 Involutometry


The terminologies used in the problem are explained in earlier chapters. Hence the figures
referred are self explanatory.
6
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram










Indian Institute of Technology Madras





























Fig. 4.3 Layout for tooth thickness determination at any point on tooth profile



- Given Data: Pressure angle, =20
o
= 0.349 rad., Z
1
= 21, m= 12mm.
- Solution:
r
1
= 0.5.m.Z
1
= 0.5 x 12 x 21=126 mm
r
b
= r
1
.Cos = 126 x cos 20
o
= 118.4 mm
a = 1m = 1 x 12 = 12 mm
r
a
= r
1
+ a = 126 + 12 = 138 mm
p
1
= .m = . 12 = 37.14 mm
t
1
= 0.5 p
1
= 0.5 x 37.14 = 18.57 mm
inv = tan - = tan 0.349 0.349 = 0.015 rad
7
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram










Indian Institute of Technology Madras

At the base circle
b
= 0, Hence tooth thickness t
b
at the base circle is:

= +
= +
t
1
t 2 r ( inv inv )
b b b
2 r
1
18.57
2x118.4 x( 0.015 0 ) 21.0 mm
2x126

| |

=


At the addendum circle the pressure angle is given by,

a
=cos
-1
(r
b
/r
a
) =cos
-1
(118.4 /138) =0.54 rad
inv
a
= tan 0.54 0.54 = 0.059

Hence tooth thickness t
a
can be calculated as,

| |
|
= +
|
\ .
t
1
t 2 r inv inv
a a
2 r
1
| |
a

Substituting the values,

| |
= + =
|
\ .
.
t x x . . . m
a
x
18 57
2 138 0 015 0 059 8 20
2 126
m


Minimum recommended top land thickness is,
t
amin
= 0.25 m = 0.25 x 12 = 3 mm

From the above, we know that, t
a
> t
amin
,

hence the tip thickness is adequate and
permissible.

-----------------------
8