MIT OpenCourseWare http://ocw.mit.

edu

5.60 Thermodynamics & Kinetics

Spring 2008

For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.

5.60 Spring 2008

Lecture #3

page 1

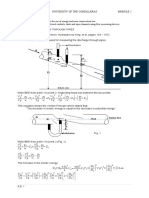
Isothermal Gas Expansion

gas (p1, V1, T) = gas (p2, V2, T)

( T = 0)

Irreversibly (many ways possible) (1) Set pext = 0

p= 0 T p= 0 p 1,V1 T p 2,V2

w (1) = pext dV = 0
V1

v2

(2)

Set pext = p2
p2 T p2 p 1,V1 T p 2,V2

w (2) = p2dV = p2 (V2 V1 )

V1

v2

p p1

p2 V1 V2

-w(2)

Note, work is negative: system expands against surroundings

5.60 Spring 2008

Lecture #3

page 2

(3)

Carry out change in two steps

gas (p1, V1, T) = gas (p3, V3, T) = gas (p2, V2, T)

p3 T p 3,V3
v3 v2

p1 > p3 > p2
p2

p3 p 1,V1

T p 2,V2

w (3) = p3dV p2dV = p3 (V3 V1 ) p2 (V2 V3 )

V1 V3

p p1 p3 p2 V1 V3 V2

More work delivered to surroundings in this case.

-w(3)
(4)
p p1

Reversible change

p = pext throughout

wrev = 2 pdV
V1

p2 V1 V2 rev

Maximum work delivered to surroundings for isothermal gas expansion is obtained using a reversible path

For ideal gas:

wrev = 2
V1

V p nRT dV = nRT ln 2 = nRT ln 2 V V1 p1

5.60 Spring 2008

Lecture #3

page 3

The Internal Energy U -q + d -w dU = d (First Law)

dU = C pathdT pext dV T ,V And U (

U U dU = dT + dV T V V T

Some frequent constraints:

Reversible

-q + d -q pdV -w = d dU = d rev rev rev -w = 0 -q = d d -q = 0 d

(p = pext )

Isolated Adiabatic Constant V

-w reversible dU = d = -pdV

-q w = 0 dU = d V
Constant V

U U dU = dT + dV T V V T but also U -q = d dT V T V

-q = C dT d V V

U = CV T V

very important result!!

So

dU = CV dT +

U V T

dV
what is this?

5.60 Spring 2008

Lecture #3

page 4

Joule Free Expansion of a Gas

(to get

U ) V T

Adiabatic
gas vac

q=0 w=0

gas (p1, T1, V1) = gas (p2, T2, V2) Since q = w = 0 Recall

Expansion into Vac. (pext=0)

dU or U = 0

Constant U

dU = CV dT +
U
V T

U dV = 0 V T

dVU = CV dTU
T V U measure in Joule exp't! T V U

U = CV V T

Joule did this.

lim V 0

T T dU = CV dT CV J dV = J V U V U Joule coefficient

For Ideal gas

U(T)

dU = CV dT

J = 0

exactly Always for ideal gas only depends on T

The internal energy of an ideal gas depends only on temperature

Consequences

U = 0

For all isothermal expansions or compressions of ideal gases

U = CV dT

For any ideal gas change in state