EE 369

POWER SYSTEM ANALYSIS

Lecture 13
Newton-Raphson Power Flow
Tom Overbye and Ross Baldick
1
Announcements
Read Chapter 12, concentrating on sections
12.4 and 12.5.
Homework 10 is 6.26, 6.28, 6.29, 6.30, 6.31,
6.36, 6.38, 6.45, 6.51, 6.53, 6.57, 12.19, 12.22,
12.24, 12.28; due Tuesday, November 27.
2
Using the Power Flow: Example 1
slack
SLACK345
SLACK138
RAY345
RAY138
RAY69
FERNA69
A
MVA
DEMAR69
BLT69
BLT138
BOB138
BOB69
WOLEN69
SHIMKO69
ROGER69
UIUC69
PETE69
HISKY69
TIM69
TIM138
TIM345
PAI69
GROSS69
HANNAH69
AMANDA69
HOMER69
LAUF69
MORO138
LAUF138
HALE69
PATTEN69
WEBER69
BUCKY138
SAVOY69
SAVOY138
JO138 JO345
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
1.02 pu
1.01 pu
1.02 pu
1.03 pu
1.01 pu
1.00 pu
1.00 pu
0.99 pu
1.02 pu
1.01 pu
1.00 pu
1.01 pu
1.01 pu
1.01 pu
1.01 pu
1.02 pu
1.00 pu
1.00 pu
1.02 pu
0.997 pu
0.99 pu
1.00 pu
1.02 pu
1.00 pu
1.01 pu
1.00 pu
1.00 pu 1.00 pu
1.01 pu
1.02 pu
1.02 pu
1.02 pu
1.03 pu
A
MVA
1.02 pu
A
MVA
A
MVA
LYNN138
A
MVA
1.02 pu
A
MVA
1.00 pu
A
MVA
218 MW
54 Mvar
21 MW
7 Mvar
45 MW
12 Mvar
140 MW
45 Mvar
37 MW
13 Mvar
12 MW
5 Mvar
150 MW
0 Mvar
56 MW
13 Mvar
15 MW
5 Mvar
14 MW
2 Mvar
42 MW
2 Mvar
45 MW
0 Mvar
58 MW
36 Mvar
36 MW
10 Mvar
0 MW
0 Mvar
22 MW
15 Mvar
60 MW
12 Mvar
20 MW
30 Mvar
23 MW
7 Mvar
33 MW
13 Mvar
16.0 Mvar 18 MW
5 Mvar
58 MW
40 Mvar 51 MW
15 Mvar
14.3 Mvar
33 MW
10 Mvar
15 MW
3 Mvar
23 MW
6 Mvar 14 MW
3 Mvar
4.8 Mvar
7.2 Mvar
12.8 Mvar
29.0 Mvar
7.4 Mvar
0.0 Mvar
106 MW
8 Mvar
20 MW
8 Mvar
150 MW
0 Mvar
17 MW
3 Mvar
0 MW
0 Mvar
14 MW
4 Mvar
Using
case
from
Example
6.13
3
Dishonest Newton-Raphson
Since most of the time in the Newton-Raphson
iteration is spent dealing with the Jacobian, one
way to speed up the iterations is to only calculate
(and factorize) the Jacobian occasionally:
known as the Dishonest Newton-Raphson or
Shamanskii method,
an extreme example is to only calculate the Jacobian
for the first iteration, which is called the chord method.
( 1) ( ) ( ) -1 ( )
( 1) ( ) (0) -1 ( )
( )
Honest: - ( ) ( )
Dishonest: - ( ) ( )
Both require ( ) for a solution
v v v v
v v v
v
c
+
+
=
=
<
x x J x f x
x x J x f x
f x
4
Dishonest Newton-Raphson
Example
2
1
( ) (0) ( )
( ) ( ) 2
(0)
( 1) ( ) ( ) 2
(0)
Use the Dishonest Newton-Raphson (chord method)
to solve ( ) 0, where:
( ) - 2
( ) ( )
1
(( ) - 2)
2
1
(( ) - 2)
2
v v
v v
v v v
f x
f x x
df
x x f x
dx
x x
x
x x x
x

+
=
=
(
A =
(

(
A =
(

(
=
(

5
Dishonest N-R Example, contd
( 1) ( ) ( ) 2
(0)
(0)
( ) ( )
1
(( ) - 2)
2
Guess 1. Iteratively solving we get
(honest) (dishonest)
0 1 1
1 1.5 1.5
2 1.41667 1.375
3 1.41422 1.429
4 1.41422 1.408
v v v
v v
x x x
x
x
x x v
+
(
=
(

=
We pay a price
in increased
iterations, but
with decreased
computation
per iteration
6
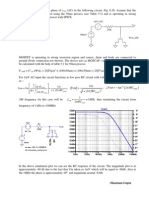
Two Bus Dishonest ROC
Slide shows the region of convergence for different initial
guesses for the 2 bus case using the Dishonest N-R
Red region
converges
to the high
voltage
solution,
while the
yellow region
converges
to the low
voltage
solution
7
Honest N-R Region of Convergence
Maximum
of 15
iterations
8
Decoupled Power Flow
The completely Dishonest Newton-
Raphson (chord) is not usually used for
power flow analysis. However several
approximations of the Jacobian matrix
are used that result in a similar
approximation.
One common method is the decoupled
power flow. In this approach
approximations are used to decouple the
real and reactive power equations.
9
Decoupled Power Flow
Formulation
( ) ( )
( )
( )
( )
( )
( ) ( ) ( )
( )
2 2 2
( )
( )
General form of the power flow problem
( )
( )
( )
where
( )
( )
( )
v v
v
v
v
v
v v v
v
D G
v
v
n Dn Gn
P P P
P P P
(
c c
(
(
( A c c
A
(
= =
(
(
(
A A ( c c (


(
c c
(

(
+
(
A =
(
(
+

P P
V
P x
f x
Q x V Q Q
V
x
P x
x
10
Decoupling Approximation
( ) ( )
( )
( )
( )
( )
( )
( )
( )
Usually the off-diagonal matrices, and
are small. Therefore we approximate them as zero:
( )
( )
( )
Then the problem
v v
v
v
v
v
v
v
v
c c
c c
(
c
(
(
( A
A
c
(
= =
(
(
(
c
A A (
(


(
c

P Q
V
P
0

P x

f x
Q
Q x V
0
V
1 1
( ) ( )
( )
( ) ( ) ( )
can be decoupled
( ), ( )
v v
v
v v v

( (
c c
A = A A = A
( (
c c

P Q
P x V Q x
V
11
Off-diagonal Jacobian Terms
( )
( )
Justification for Jacobian approximations:
1. Usually , therefore
2. Usually is small so sin 0
Therefore
cos sin 0
cos sin 0
ij ij
ij ij
i
i ij ij ij ij
j
i
i j ij ij ij ij
j
r x G B
V G B
V V G B
u u
u u
u u
~
c
= + ~
c
c
= + ~
c
P
V
Q

12
Decoupled N-R Region of
Convergence
13
Fast Decoupled Power Flow
By further approximating the Jacobian we obtain
a typically reasonable approximation that is
independent of the voltage magnitudes/angles.
This means the Jacobian need only be built and
factorized once.
This approach is known as the fast decoupled
power flow (FDPF)
FDPF uses the same mismatch equations as
standard power flow so it should have same
solution if it converges
The FDPF is widely used, particularly when we
only need an approximate solution.
14
FDPF Approximations
( ) 1 ( ) 1 ( )
( )
1 ( ) 1 ( )
The FDPF makes the following approximations:
1. 0
2. 1 (for some occurrences),
3. sin 0 cos 1
Then: {| | } ( ),
{| | } ( )
Where is just the imaginary pa
ij
i
ij ij
v v v
v
v v
G
V
diag
diag
u u


=
=
= =
A = A
A = A
B V P x
V B V Q x
B
bus bus bus
bus
( )
rt of the ,
except the slack bus row/column are omitted. That is,
is , but with the slack bus row and column deleted.
Sometimes approximate {| | } by identity.
v
j
diag
= + Y G B
B B
V
15
FDPF Three Bus Example
Line Z = j0.07
Line Z = j0.05 Line Z = j0.1
One Two
200 MW
100 MVR
Three 1.000 pu
200 MW
100 MVR
Use the FDPF to solve the following three bus system
34.3 14.3 20
14.3 24.3 10
20 10 30
bus
j

(
(
=
(

(

Y
16
FDPF Three Bus Example, contd
1
(0)
(0)
2
2
3
3
34.3 14.3 20
24.3 10
14.3 24.3 10
10 30
20 10 30
0.0477 0.0159
0.0159 0.0389
Iteratively solve, starting with an initial voltage guess
0 1
0 1
bus
j
V
V
u
u

(

(
(
= =
(
(

(


(
=
(


(
( (
= =
(
( (


Y B
B
(1)
2
3
0 0.0477 0.0159 2 0.1272
0 0.0159 0.0389 2 0.1091
u
u
(
(


( ( ( ( (
= + =
( ( ( ( (


17
FDPF Three Bus Example, contd
(1)
2
3
1
(2)
2
3
1 0.0477 0.0159 1 0.9364
1 0.0159 0.0389 1 0.9455
( )
( cos sin )
0.1272 0.0477 0.0159
0.1091 0.0159 0.0389
n
i Di Gi
k ik ik ik ik
i i k
V
V
P x P P
V G B
V V
u u
u
u
=
(
( ( ( (
= + =
(
( ( ( (



A
= + +

( ( (
= +
( ( (

(2)
2
3
0.151 0.1361
0.107 0.1156
0.924
0.936
0.1384 0.9224
Actual solution:
0.1171 0.9338
V
V

( (
=
( (

(
(
=
(
(

( (
= =
( (

V
18
FDPF Region of Convergence
19
DC Power Flow
The DC power flow makes the most severe
approximations:
completely ignore reactive power, assume all the
voltages are always 1.0 per unit, ignore line
conductance
This makes the power flow a linear set of
equations, which can be solved directly:
1
= B P
20
DC Power Flow Example
21
= AP
DC Power Flow 5 Bus Example
slack
One
Two
Three Four Five
A
MVA
A
MVA
A
MVA
A
MVA
A
MVA
1.000 pu 1.000 pu
1.000 pu
1.000 pu
1.000 pu
0.000 Deg -4.125 Deg
-18.695 Deg
-1.997 Deg
0.524 Deg
360 MW
0 Mvar
520 MW
0 Mvar
800 MW
0 Mvar
80 MW
0 Mvar
Notice with the dc power flow all of the voltage magnitudes are
1 per unit.
22
Power System Control
A major problem with power system operation is
the limited capacity of the transmission system
lines/transformers have limits (usually thermal)
no direct way of controlling flow down a
transmission line (e.g., there are no low cost valves
to close to limit flow, except on and off)
open transmission system access associated with
industry restructuring is stressing the system in new
ways
We need to indirectly control transmission line
flow by changing the generator outputs.
23
Indirect Transmission Line Control
What we would like to determine is how a change in
generation at bus k affects the power flow on a line
from bus i to bus j.
The assumption is
that the change
in generation is
absorbed by the
slack bus
24
Power Flow Simulation - Before
One way to determine the impact of a generator
change is to compare a before/after power flow.
For example below is a three bus case with an
overload.
Z for all lines = j0.1
One Two
200 MW
100 MVR
200.0 MW
71.0 MVR
Three 1.000 pu
0 MW
64 MVR
131.9 MW
68.1 MW
68.1 MW
124%
25
Power Flow Simulation - After
Z for all lines = j0.1
Limit for all lines = 150 MVA
One Two
200 MW
100 MVR
105.0 MW
64.3 MVR
Three
1.000 pu
95 MW
64 MVR
101.6 MW
3.4 MW
98.4 MW
92%
100%
Increasing the generation at bus 3 by 95 MW
(and hence decreasing generation at the slack
bus 1 by a corresponding amount), results in a
31.3 MW drop in the MW flow on the line from
bus 1 to 2.
26
Analytic Calculation of Sensitivities
Calculating control sensitivities by repeated
power flow solutions is tedious and would
require many power flow solutions.
An alternative approach is to analytically
calculate these values
The power flow from bus i to bus j is
sin( )
So We just need to get
i j i j
ij i j
ij ij
i j ij
ij
ij Gk
V V
P
X X
P
X P
u u
u u
u u u

~ ~
A A A
A ~
A
27
Analytic Sensitivities
1
From the fast decoupled power flow we know
( )
So to get the change in due to a change of
generation at bus , just set ( ) equal to
all zeros except a minus one at position .
0
1
0
k
k

A = A
A
A

A =

B P x

P x
P Bus

k
(
(
(

(
(
(
(

28
Three Bus Sensitivity Example
line
bus
1
2
3
For the previous three bus case with Z 0.1
20 10 10
20 10
10 20 10
10 20
10 10 20
Hence for a change of generation at bus 3
20 10 0 0.0333
10 20 1 0.0667
j
j
u
u

=

(

(
(
= =
(
(

(

A
( ( (
= =
( ( (
A

Y B
3 to 1
3 to 2 2 to 1
0.0667 0
Then 0.667 pu
0.1
0.333 pu 0.333 pu
P
P P
(
(

A = =
A = A =
29