Professional Documents
Culture Documents
Module 2 - GEARS: L Hfwxuh 13 - Bevel Gears RQWHQWV
Module 2 - GEARS: L Hfwxuh 13 - Bevel Gears RQWHQWV
Uploaded by
sunita45Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Module 2 - GEARS: L Hfwxuh 13 - Bevel Gears RQWHQWV
Module 2 - GEARS: L Hfwxuh 13 - Bevel Gears RQWHQWV
Uploaded by
sunita45Copyright:
Available Formats
Machine Design II Prof. K.Gopinath & Prof. M.M.
Mayuram
Indian Institute of Technology Madras
Module 2 - GEARS
L 13 BEVEL GEARS
C
13.1 Bevel gear introduction
13.2 Bevel gear geometry and terminology
13.3 Bevel gear force analysis
13.4 Bending stress analysis
13.5 Contact stress analysis
13.6 Permissible bending fatigue stress
13.7 Permissible contact fatigue stress
13.1 INTRODUCTION
(a) (b)
(c) (d)
Fig.13.1 (a) Bevel gear, (b) Straight bevel gear, (c) Spiral bevel gear (d) Hypoid
gear
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Bevel gears transmit power between two intersecting shafts at any angle or between
non- intersecting shafts. They are classified as straight and spiral tooth bevel and
hypoid gears as in Fig.13.1
13.2 GEOMETRY AND TERMINOLOGY
Fig.13.2 Bevel gear in mesh
When intersecting shafts are connected by gears, the pitch cones (analogous to the
pitch cylinders of spur and helical gears) are tangent along an element, with their
apexes at the intersection of the shafts as in Fig.13.2 where two bevel gears are in
mesh.
The size and shape of the teeth are defined at the large end, where they intersect the
back cones. Pitch cone and back cone elements are perpendicular to each other. The
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
tooth profiles resemble those of spur gears having pitch radii equal to the developed
back cone radii r
bg
and r
bp
and are shown in Fig. 13.3. which explains the
nomenclatures of a bevel gear.
Fig. 13.3 Bevel gear nomenclature
b1 1
v1
1
2r Z
Z = =
p cos
(13.1)
(13.2)
b2 2
Z =
v2
2r Z
=
p cos
where Z
v
is called the virtual number of teeth, p is the circular pitch of both the
imaginary spur gears and the bevel gears. Z
1
and Z
2
are the number of teeth on the
pinion and gear,
1
and
2
are the pitch cone angles of pinion and gears. It is a practice
to characterize the size and shape of bevel gear teeth as those of an imaginary spur
gear appearing on the developed back cone corresponding to Tredgolds
approximation.
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
a) Bevel gear teeth are inherently non - interchangeable.
b) The working depth of the teeth is usually 2m, the same as for standard spur and
helical gears, but the bevel pinion is designed with the larger addendum ( 0.7
working depth).
c) This avoids interference and results in stronger pinion teeth. It also increases the
contact ratio.
d) The gear addendum varies from 1m for a gear ratio of 1, to 0.54 m for ratios of
6.8 and greater.
The gear ratio can be determined from the number of teeth, the pitch diameters or the
pitch cone angles as,
(13.3)
1 1 2 2
2 1
2 2 1 1
n Z d
i = = = = =tan =cot
n Z d
Accepted practice usually imposes two limits on the face width
(13.4)
Where L is the cone distance. Smaller of the two is chosen for design.
L
b 10m and b
3
Fig. 13.4 Illustration of spiral angle
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
The Fig.13.4 illustrates the measurement of the spiral angle of a spiral bevel gear.
Bevel gears most commonly have a pressure angle of 20
o
, and spiral bevels usually
have a spiral angle of 35
o
.
Fig.13.5 Zero bevel gears
The Fig.13.5 illustrates Zero bevel gears, which are having curved teeth like spiral
bevels. But they have a zero spiral angle.
Fig. 13.6 Comparison of intersecting and offset shaft bevel type gearings
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
(a) (b) (c)
(d) (e) (f)
Fig.13.7 Different types of bevel gears (a) Usual form, (b) Miter gears,
(c), (d), (e) Crown gear, (f) Internal bevel gear
13.3 FORCE ANALYSIS
Fig. 13.8 Gear tooth forces
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Fig. 13.9 Gear and shaft forces
Fig. 13.10 Bevel gear - Force analysis
In Fig. 13.10, F
n
is normal to the pitch cone and the resolution of resultant tooth force F
n
into its tangential (torque producing), radial (separating) and axial (thrust) components
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
is designated F
t
, F
r
and F
a
respectively. An auxiliary view is needed to show the true
length of the vector representing resultant force F
n
(which is normal to the tooth profile).
Fig. 13.11 Linear tooth force distribution
Resultant force F
n
is shown applied to tooth at the pitch cone surface and midway along
tooth width b. It is also assumed that load is uniformly distributed along the tooth width
despite the fact that the tooth width is larger at the outer end.
av
d =d-bsin
(13.5)
(13.6)
av
av
d n
V =
6000
(13.7)
t
av
1000W
F =
v
Where V
av
is in meters per second, d
av
is in meters, n is in revolutions per minute, F
t
is
in N and W is power in kW.
(13.8)
(13.9)
(13.10)
n t
r n t
a n t
F = F /cos
F = F cos = F tan cos
F = F sin = F tan sin
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
For spiral bevel gear,
(13.11)
(13.12)
t
r n
a t n
F
F = ( tan cos sin sin )
cos
F ( tan sin sincos
F = )
Where is used in the preceding equation, the upper sign applies to a driving
pinion with right-hand spiral rotating clockwise as viewed from its large end and to a
driving pinion with left-hand spiral rotating counter clock-wise when viewed from its
large end. The lower sign applies to a left-hand driving pinion rotating clockwise and to
a driving pinion rotating counter clockwise. Similar to helical gears,
n
is the pressure
angle normal measured in a plane normal to the tooth.
or
13.4 TOOTH BENDING STRESS
The equation for bevel gear bending stress is the same as for spur gears as shown
below:
t
b v o m
F
= K K K (13.13)
bmJ
Where, F
t
=Tangential load in N
m = module at the large end of the tooth in mm
b = Face width in mm
J = Geometry form factor based on virtual number of teeth from Fig. 13.12 and 13.13.
K
v
= Velocity factor, from Fig.13.14.
K
o
= Overload factor, Table 13.1.
K
m
= Mounting factor, depending on whether gears are straddle mounted (between two
bearings) or overhung (outboard of both bearings), and on the degree of mounting
rigidity as shown in Table 13.2.
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Fig. 13.12 Number of teeth in gear for which geometry factor
J is desired, pressure angle 20
o
and shaft angle 90
o
Fig.13.13 Number of teeth in gear for which geometry factor J
is desired, pressure angle 20
o
, spiral angle 35
o
and shaft angle 90
o
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Fig.13.14 Dynamic load factor, K
v
Table 13.1 -Overload factor K
o
Driven Machinery
Source of power Uniform Moderate Shock Heavy Shock
Uniform 1.00 1.25 1.75
Light shock 1.25 1.50 2.00
Medium shock 1.50 1.75 2.25
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Table 13.2 Mounting factor K
m
for bevel gears
Mounting type Mounting rigidity
Maximum to questionable
Both gears are straddle-
mounted
One gear straddle-mounted;
the other overhung
Both gear overhung
1.0 to 1.25
1.1 to 1.4
1.25 to 1.5
13.6 PERMISSIBLE TOOTH BENDING STRESS (AGMA)
Fatigue strength of the material is given by:
e
=
e
k
L
k
v
k
s
k
r
k
T
k
f
k
m
(13.14)
Where,
e
endurance limit of rotating-beam specimen
k
L
= load factor, = 1.0 for bending loads
k
v
= size factor, = 1.0 for m < 5 mm and
= 0.85 for m > 5 mm
k
s
= surface factor, taken from Fig.13.15 based on the ultimate strength of the material
and for cut, shaved, and ground gears.
k
r
= reliability factor given in Table 13.3.
k
T
= temperature factor, = 1 for T 120
o
C and more than 120
o
C, k
T
< 1 to be taken from
AGMA standards
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Fig.13.15 Surface factor, K
s
Table 13.3 Reliability factor K
r
Reliability factor R 0.50 0.90 0.95 0.99 0.999 0.9999
Factor Kr 1.000 0.897 0.868 0.814 0.753 0.702
k
f
= fatigue stress concentration factor. Since this factor is included in J factor its value
is 1.
a.
k
m
= Factor for miscellaneous effects. For idler gears subjected to two way bending, =
1. For other gears subjected to one way bending, the value is taken fromFig.13.16. Use
k
m
= 1.33 for
ut
less than 1.4GP
Fig.13.16 Miscellaneous effects factor K
m
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Permissible bending stress is given by
(13.15)
e
b
[ ]=
s
Hence the design equation from bending consideration is,
b
[b ] (13.16)
Bevel gear surface fatigue stress can be calculated as for spur gears, with only two
modifications.
t
H p V o m
F
=C K K K
bdI
(13.17)
13.7 CONTACT STRESS:
1.23 times the C
p
values given in the Table13.4 are taken to account for a somewhat
more localized contact area than spur gears.
Table 13.4 Elastic Coefficient Cp for spur gears, in (MPa)
0.5
Gear material Pinion Material
( = 0.3 in all cases) Steel Cast iron Al Bronze Tin Bronze
Steel, E=307GPa 191 166 162 158
Cast iron, E = 131GPa 166 149 149 145
Al Bronze, E = 121GPa 162 149 145 142
Tin Bronze, E = 110GPa 158 145 141 137
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Fig.13.17 Geometry factor I for straight bevel gear pressure angle 20
o
and shaft
angle 90
o
Fig.13.18 Geometry factor I for spiral bevel gear pressure angle 20
o
, spiral angle
35
o
and shaft angle 90
o
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
Surface fatigue strength of the material is given by,
sf
=
sf
K
L
K
H
K
R
K
T
(13.18)
Where
sf
= surface fatigue strength of the material given in Table 13.7
K
L
= Life factor given in Fig.13.19
Table 13.7 Surface fatigue strength
sf
(MPa) for metallic spur gear,
(10
7
cycle life 99% reliability and temperature < 120
o
C)
Material sf (MPa)
Steel 2.8 (Bhn) 69 MPa
Nodular iron 0.95 [ 2.8 (Bhn) 69 MPa]
Cast iron, grade 20 379
Cast iron, grade 30 482
Cast iron, grade 40 551
Tin Bronze, AGMA 2C ( 11% Sn) 207
Aluminium Bronze (ASTM b 148 52) (Alloy 9C H.T ) 448
Fig.13.19 Life factor K
L
Machine Design II Prof. K.Gopinath & Prof. M.M.Mayuram
Indian Institute of Technology Madras
K
H
is hardness ratio factor, K the Brinell hardness of the pinion by Brinell hardness of
the gear as given in Fig. 13.20.
K
H
= 1.0 for K < 1.2
K
R
= Reliability factor, given in Table 13.3.
Fig.13.20 Hardness ratio factor, K
H
K
T
= temperature factor,
= 1 for T 120
o
C based on lubricant temperature.
Above 120
o
C, it is less than 1 to be taken from AGMA standards.
Allowable surface fatigue stress for design is given by
[
H
] =
Sf
/ s (13.19)
Factor of safety s = 1.1 to 1.5
Hence Design equation is:
H
[
H
] (13.20)
------------------
You might also like
- Gear DesignDocument83 pagesGear DesignmuhammadaminjamalmutNo ratings yet
- Gear2 02aDocument5 pagesGear2 02aΚυριάκος ΒαφειάδηςNo ratings yet
- Bevel Gear Load CapacityDocument11 pagesBevel Gear Load CapacityAriel Rasjido50% (2)
- Gear Generating Profile Shift CalculationsDocument2 pagesGear Generating Profile Shift CalculationsSanjay Shelar0% (1)
- Design & Validation of Eot CraneDocument106 pagesDesign & Validation of Eot CraneNishadhraj Vasava92% (13)
- Non Linear Analysis of Spur Gear Using Matlab CodeDocument105 pagesNon Linear Analysis of Spur Gear Using Matlab CodeArvind Kumar Yadav100% (2)
- The Effect of Center Distance Change On Gear Teeth EngagementDocument21 pagesThe Effect of Center Distance Change On Gear Teeth EngagementDavide MaranoNo ratings yet
- Gear Force & StressDocument30 pagesGear Force & StressRanjeethkumar JalalNo ratings yet
- Spur Gear (Treb)Document19 pagesSpur Gear (Treb)diiivadNo ratings yet
- Bevel ExplanationDocument4 pagesBevel ExplanationVarun VaidyaNo ratings yet
- Farm House PlanDocument8 pagesFarm House Planparesh09No ratings yet
- Example Problem 9.1 GivenDocument12 pagesExample Problem 9.1 GivengertjaniNo ratings yet
- Deflection Calculation Due To Imposed Load On Corridor JoistDocument14 pagesDeflection Calculation Due To Imposed Load On Corridor JoistranjitNo ratings yet
- Tut 001 TwoStageHelicalGearbox EDocument31 pagesTut 001 TwoStageHelicalGearbox Eardec_8No ratings yet
- FEA Report PDFDocument24 pagesFEA Report PDFDanish JavedNo ratings yet
- Furniture DesignDocument26 pagesFurniture Designparesh09100% (3)
- Contact Stress in Helical Bevel GearsDocument16 pagesContact Stress in Helical Bevel GearsBiden Le0% (1)
- Pressure Vessel Inspection ReportDocument33 pagesPressure Vessel Inspection ReportJinlong SuNo ratings yet
- Bond-Slip Model For Detailed Finite-Element AnalysisDocument10 pagesBond-Slip Model For Detailed Finite-Element AnalysisSilver rayleighNo ratings yet
- Spur Gear Design by IIT MadrasDocument28 pagesSpur Gear Design by IIT MadrasC.S.ABHILASHNo ratings yet
- Terminal Report ShredderDocument25 pagesTerminal Report ShredderEnriv YasiladNo ratings yet
- 2015 - Finite Element Modelling of Debonding Failures in Steel Beams Flexurally Strengthened With CFRP Laminates - Teng Fernando Yu PDFDocument12 pages2015 - Finite Element Modelling of Debonding Failures in Steel Beams Flexurally Strengthened With CFRP Laminates - Teng Fernando Yu PDFvlad lupasteanuNo ratings yet
- Designing Parametric Bevel Gears With Catia V5: 1 Sources, Credits and LinksDocument10 pagesDesigning Parametric Bevel Gears With Catia V5: 1 Sources, Credits and Linksimrans04No ratings yet
- Bevel GearsDocument1 pageBevel GearsBalasoobramaniam CarooppunnenNo ratings yet
- Modal Space - in Our Own Little World: by Pete AvitabileDocument2 pagesModal Space - in Our Own Little World: by Pete AvitabileVignesh SelvarajNo ratings yet
- Bev Gear Design PDFDocument5 pagesBev Gear Design PDFMawan BentzNo ratings yet
- BevelDocument20 pagesBevelOmer NadeemNo ratings yet
- Measuring Helix Angle of GearsDocument6 pagesMeasuring Helix Angle of Gearsdarshan.hegdebNo ratings yet
- Design-II, 2016 Bevel Gear Design ProcedureDocument1 pageDesign-II, 2016 Bevel Gear Design ProcedureenggsantuNo ratings yet
- A Procedure To Determine The Unknown Geometry of External Cylindrical Gears - Gear Solutions Magazine Your Resource To The Gear IndustryDocument11 pagesA Procedure To Determine The Unknown Geometry of External Cylindrical Gears - Gear Solutions Magazine Your Resource To The Gear IndustryChetan PrajapatiNo ratings yet
- 10.1 - Calculation of Strength For Spur and Helical Gears - TechnicalData - KGSTOCKGEARS PDFDocument14 pages10.1 - Calculation of Strength For Spur and Helical Gears - TechnicalData - KGSTOCKGEARS PDFChetan NeheteNo ratings yet
- Loads Acting On Crane Structure During TravelDocument11 pagesLoads Acting On Crane Structure During Travelaiyubi2No ratings yet
- Spur GearsDocument8 pagesSpur GearstopjobNo ratings yet
- Worm Gear CalculationDocument16 pagesWorm Gear Calculationprashasscribd100% (1)
- Addendum Modified Gear For An All-Terrain Vehicle GearboxDocument6 pagesAddendum Modified Gear For An All-Terrain Vehicle GearboxIJRASETPublicationsNo ratings yet
- Cycloid Drive - Replaced by Planocentric Involute GearingDocument6 pagesCycloid Drive - Replaced by Planocentric Involute GearingMax GrandeNo ratings yet
- Optimization of Gear Reduction Unit Through Ray DiagramDocument7 pagesOptimization of Gear Reduction Unit Through Ray Diagramأحمد دعبس100% (1)
- Subroutine For Cohesive ElementDocument41 pagesSubroutine For Cohesive ElementBhushanRaj100% (1)
- Bevel GearDocument28 pagesBevel Gearmahesh kitturNo ratings yet
- MESYS Shaft CalculationDocument51 pagesMESYS Shaft Calculationdd hhNo ratings yet
- Trocoide Thurman PDFDocument4 pagesTrocoide Thurman PDFmgualdiNo ratings yet
- Bevel GearDocument13 pagesBevel GearADII 2701No ratings yet
- MESYS Shaft CalculationDocument28 pagesMESYS Shaft CalculationZoebairNo ratings yet
- Contact Stress Analysis of Spur Gear Teeth Pair PDFDocument6 pagesContact Stress Analysis of Spur Gear Teeth Pair PDFCan CemreNo ratings yet
- Thesis Mochammad Rizky DiprasetyaDocument125 pagesThesis Mochammad Rizky DiprasetyaRizky DsNo ratings yet
- Brake Calculation SheetDocument2 pagesBrake Calculation SheetvijayNo ratings yet
- Home Search Collections Journals About Contact Us My IopscienceDocument8 pagesHome Search Collections Journals About Contact Us My IopscienceCan CemreNo ratings yet
- Comparison of AGMA .2001, and ISO, 6336 Ratings Tor Four Gear Sets-McvittieDocument4 pagesComparison of AGMA .2001, and ISO, 6336 Ratings Tor Four Gear Sets-McvittiewholenumberNo ratings yet
- 226 - Shaking Table Testing of A Steel Framce Structure...Document9 pages226 - Shaking Table Testing of A Steel Framce Structure...Ing Jaime Espinoza SkinfieldNo ratings yet
- A Crowning Achievement For Automotive ApplicationsDocument10 pagesA Crowning Achievement For Automotive ApplicationsCan CemreNo ratings yet
- Pages From Hyundai Welding Handbook (2006)Document1 pagePages From Hyundai Welding Handbook (2006)tuatkNo ratings yet
- Characteristics of Trochoids and Their Application To Determining Gear Teeth Fillet ShapesDocument14 pagesCharacteristics of Trochoids and Their Application To Determining Gear Teeth Fillet ShapesJohn FelemegkasNo ratings yet
- Gear Technical Inquiry Doc 00032Document3 pagesGear Technical Inquiry Doc 00032Sanjay ShelarNo ratings yet
- Tseng 2004 Mechanism and Machine TheoryDocument15 pagesTseng 2004 Mechanism and Machine TheoryKhanh VqNo ratings yet
- Design For Fatigue and Simulation of Glass Fibre Epoxy Composite Automobile Leaf SpringDocument22 pagesDesign For Fatigue and Simulation of Glass Fibre Epoxy Composite Automobile Leaf SpringjonNo ratings yet
- THESIS - PHD - TE IN SPUR GEARS - STATIC AND DYNAMIC FINITE ELEMENT MODELLING AND DESIGN OPTIMISATION PDFDocument267 pagesTHESIS - PHD - TE IN SPUR GEARS - STATIC AND DYNAMIC FINITE ELEMENT MODELLING AND DESIGN OPTIMISATION PDFAsha Venkataram100% (1)
- Module 2 - GEARSDocument17 pagesModule 2 - GEARSCollin FarNo ratings yet
- Spur GearDocument11 pagesSpur GearvenkatkavinNo ratings yet
- Spur Gear PDFDocument11 pagesSpur Gear PDFegsamitNo ratings yet
- Spur Gear DesignDocument15 pagesSpur Gear DesignMaharaja KanthasamyNo ratings yet
- HTTP WWW - Google.co - in Url Q HTTP Nptel - Iitm.ac - in Courses IIT-MADRAS Machine Design II PDF 2 7Document15 pagesHTTP WWW - Google.co - in Url Q HTTP Nptel - Iitm.ac - in Courses IIT-MADRAS Machine Design II PDF 2 7fiemsabyasachiNo ratings yet
- Gear ShavingDocument6 pagesGear ShavingRuchira Chanda InduNo ratings yet
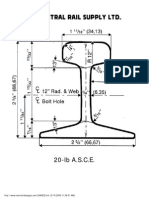
- 20 LBDocument1 page20 LBparesh09No ratings yet
- Variable Frequency DrivesDocument3 pagesVariable Frequency Drivesparesh09No ratings yet
- Slip Ring Vs Sq. CageDocument1 pageSlip Ring Vs Sq. Cageparesh09No ratings yet
- Check List For EOT CraneDocument1 pageCheck List For EOT Craneparesh09100% (1)
- Comparistion of Hydra Crane and Gantry CraneDocument1 pageComparistion of Hydra Crane and Gantry Craneparesh09No ratings yet