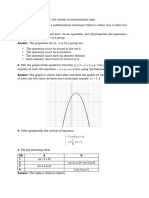
I considered (x+a)(x+b)(x+c)d form of a cubic rather than

ax^3+bx^2+cx+d because if I am working with form 1, I can "fit" my cubic

to the desired characteristics simply by "plugging in" values of a,b,c when
roots of the cubic are specified.

(a) Any cubic of the form (x+1)(x-1)(x+a)b, where a and b are real numbers
("a" may not be a complex number, as then the cubic would only have one
complex root. But by the fundamental theorem of algebra, complex roots
occur in conjugate pairs.) As a and b may be any real numbers the curve
described in (a) is not unique.

(b) Any cubic of the form a(x)(x+3)^2 will satisfy (b). where a is a real
number.(b) is not unique. (as "a" may vary). To justify why I chose to "repeat
my (x+3) term, I will use some calculus. Consider the expression y= c(x+b)
(x+a)^2. On differentiating this expression we find, dy/dx = c(x+a)
(a+2b+3x). Notice that dy/dx=0 at x=-a. (The repeated root). Furthermore,
d^2y/dx^2 at x=-a, is 2c(b-a). For all a is not equal to b, this is a maximum
or minimum point. Coupled with the fact that x=-a is a root, we fulfill the
"only touching the x axis" criteria. However if a=b, we have a "saddle point"
or "point of inflection" at x=a, in which case the cubic actually does intersect
the x axis at x=-a. This can be proven by looking at the third derivative of the
cubic which is 6c. This shows that the second derivative function is either
increasing or decreasing, and since the derivative is zero at x=-a we have a
change in concavity (or a point of inflection). So if we want a cubic to only
"touch the x axis" at a point x=-a, the cubic must be of the form (x+a)^2
(x+b)c, where c is not zero, and b does not equal a.

(c) When thinking about this, I initially put it in the form (x-2)^2(x+a)b. The
reason I used the repeated root is justified above. a cannot equal -2, as then
we would have another saddle point or "point of inflection". We also want our
cubic to equal 12 at x=0. Plugging this in we get, -4ab=12, or simply ab=-3.
a may not be complex as complex roots occur in conjugate pairs and we
already have two real roots (by FTA we may only have three roots in total for
an order three polynomial). Thus if a and b are real solutions to ab=-3 where
a and b are non zero and b does not equal 1.5, as if b =1.5 we have a=-2 and
a saddle point, then we will have a cubic that fulfills this condition. So no, not
unique.

(d) This is an interesting condition. So we have (x+a)(x+b)(x+c)d=-6 at x=0.

so abcd=-6. Rearranging abc=-6/d . as a,b,c are all integers, by closure we
have abc is an integer and -6/d is an integer. So we only have finitely many
"d" values we may pick. These are all the factors of 6. 6 has a prime
decomposition of 3*2 . Thus it's only factors are 1,6,2,3. So d may only be +1,+-6,+-2,+-3. Let us attempt to work out all abc such that this is satisfied. If
abc=+-1, We may only have 6 different possibilities. I will write these
possibilities in the form (a,b,c) from now on. (1,1,1), (-1,1,1), (1,-1,1), (1,1,-1).
abc=+6, (3,2,1),(3,1,2),(2,3,1),(2,1,3),(1,2,3),(1,3,2), (3! different
possibilities) + (1,1,6),(1,6,1),(6,1,1) (3!/2!) different possibilities. If we wish
abc=-6 it is similar but with one entry negative for each possibility. So in total
there will be 3*(no of possibilities for abc=+6 = 3(3!+3) = 3(9) = 27 different
combinations. So in total we have 27+9=36 different combinations. If abc=
+2, we have (1,1,2), (1,2,1),(2,1,1) (3!/2!) possibilities, and for abc=-2 3*(no.
of possibilities for abc=+2) = 9 possibilities, meaning 12 possibilities in total.
For abc=+-3 we solve it similarly (3 is a prime number) and we will again
have 12 possibilities in total. ALSO a,b,c may NOT be zero. So these cubics
will not touch the origin (0,0).

(e) This is the same as condition c, with different values of x and y intercepts.
Solving similarly, we have ((x-1)^2)(x+a)b = 5 at x=0. This yields ab=5.
Again, a may not be complex for the same reason stated above. And thus b
may not be complex. So the solutions are a,b are not zero, b cannot be equal
to -5 ( as then a=-1 and we have a saddle point). So for any a,b that satisfy
the above conditions (non zero, b is not -5) this condition is fulfilled.

Thank you for taking the time to read my solution! I apologize if there are any
errors in my calculation