Math 119A Homework 10 Page |1

Exercise 3.4F7: Let D be the size of a population of deer, and M the population of moose in the
same area. The Lotka–Volterra competition model for these species might look like the
following:
𝐷𝐷′ = 0.3𝐷𝐷 − 0.05𝐷𝐷2 − 0.03𝐷𝐷𝐷𝐷
𝑀𝑀′ = 0.2𝑀𝑀 − 0.04𝑀𝑀2 − 0.02𝐷𝐷𝐷𝐷
a) Plot the nullclines of this system by hand with D on the horizontal axis and M on the vertical,
similar to figure 3.24 on page 142.

b) Use the nullclines and/or algebra to find the equilibrium points of the system.

equilibrium points: (0,0), (6,0),(0,5),(30/7, 20/7)

c) Sketch the direction of the change vectors along each nullcline. Then, fill in the
change vectors in the rest of the vector field. Fill this in on your figure from part (a) similar to
figure 3.25. You can either use Sagemath to generate a vector field to get this, or you can use
the method spelled out in the text with test points.

d) Use your sketch of the vector field to determine the type of each equilibrium point.
Put the equilibria on your plot from part (a), and label each with its type.
(Stable node, Unstable Node, Unstable Node, Saddle point, Stable Spiral, Unstable Spiral , Center) (SN,UN,SP,SS,US,C).

e) What will happen to these two populations in the long run? Can they coexist?
In the long run, depending on the starting point, it should either be all moose or all deer population.
The two can coexist because the vector field shows a stable spiral

Math 119A Homework 10 Page |1

Math 119A Homework 10 Page |2

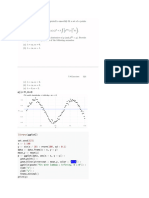
Use the figure above to determine the basin of attraction for the stable equilibrium at X=0 for the Allee
population model. (page 148)

The basin of attraction for x=0 is anywhere between 0 and a

This problem from page 151 refers to the lac Operan model on pages 149-151

The way the lactose concentration is changing when the red and blue curves cross is that, at all 3 crossing
points, the rate of change and rate are balanced

Math 119A Homework 10 Page |2