Worked solutions

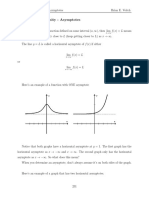
5 Measuring change: differentiation

Skills check since lim − = −∞ and lim + = ∞

x →− 3 x →− 3
−3 − 0 3
1 a = and lim− = ∞ and lim+ = −∞
−4 − 0 4
x→ 3 x→ 3

−1 − 2 12
b = − Horizontal asymptote at y = −1
4 − ( − 34 ) 19
since lim g(x ) = −1
x →±∞
1
2 a 7 x = 7x 2
3 Vertical asymptote at x = 1
1
b = x −2 since lim− f (x ) = ∞ and lim+ f ( x ) = −∞
x2 x →1 x →1

8 8 − 23 Horizontal asymptote at y = −1
c = x
5 x 3 5 since lim h(x ) = −1
x →±∞

3 4 Vertical asymptotes at x = ± 2
since lim − = ∞ and lim + = −∞
x →− 2 x →− 2

and lim− = ∞ and lim+ = −∞

x→ 2 x→ 2

Horizontal asymptote at y = 0
 5x 
since lim  − 2 =0
 x − 2
x →±∞

Exercise 5C
4 Since | 12 |< 1, 1 f= x 7 −1 7 x 6
'(x ) 7=
n n
∞
1
∞
1 5(1) 2=
f '(x ) 18
= x18 −1 18 x17
∑ 5 =
5∑ =

2

n 02
= 10
1 − 12
=n 0= 1 − 1 −1 1 −3
3 f '(x ) =
− x 2 = − x 2
2 2
Exercise 5A 1 1 1 −1 1 − 4
4 5
f (x) = x =x 5 ⇒ f '(x ) =x 5 =x 5
1 (
lim x 2 +
x →3−
= 1 )
lim+ x 2 +
= 1 10
x →3
( ) 5 5
1 −1 1 − 1 −1 1 −3
5 f (x ) == x 2 ⇒ f '(x ) =
− x 2 = − x 2
2 lim− (5 − 2 x )= lim+ (5 − 2 x )= 3 x 2 2
x →1 x →1

 2x 2 − x   2x 2 − x 
3 3 3 −1 3 − 1
3 lim−  6 f (x) =4
x3 =x 4 ⇒ f '(x ) = x 4 = x 4
 = lim+   = −1 4 4
x →0
 x  x →0  x 
 x2 − x   x2 − x 
4 lim
=   lim
=   1 Exercise 5D
 x − 1  x →1  x − 1 
− +
x →1
dy
1 a = 4x 3 − x
dx
Exercise 5B b f (x )= 5x(x 2 − 1)= 5x 3 − 5x
1
1 Vertical asymptote at x = ∴ f '(x ) = 15x 2 − 5
6
since lim− f (x ) = −∞ and lim+ f ( x ) = ∞ ds
c '(x ) 24 x 3 − 6 x
f= d = 4t + 3
x → 16 x → 16 dt
1 dv dc
Horizontal asymptote at y = e = −9.8 f = 24
2 dt dx
1
since lim f ( x ) =
x →±∞ 2
2 Vertical asymptotes at x = ± 3

© Oxford University Press 2019 Worked solutions 1

 Worked solutions

8
1 −1
2 a f=
(x ) 6=x 6 x 2 ∴ f '(x ) =
3x 2 1 − 21
c f (x ) =4 x + =x 4 + 8 x
5 3
−2 x
b =
f (x ) 5= x 3 5x 5 ∴ f '(x ) =
3x 5
1 − 34 −3
1 ∴ f '(x ) = x − 4x 2
2 4
c f (x) = − 3 x =
2 x −1 − 3x 2
x 1 −3 −3 15
so f '(1) = (1) 4 − 4(1) 2 =
−
3 − 12 4 4
∴ f '(x) =
−2 x −2 − x
2 2 f '(x ) = 2 x 2 − 9 x − 3 ∴ 2= 2 x 2 − 9 x − 3
3 3 −2
3 a (x)
f= = −3x −3
x ∴ f '(x ) =
2x 2 2 ⇒ 2 x 2 − 9 x − 5= (2 x + 1)(x − 5)= 0
3 3 3 −2
b f=
(x) = = x 1
(2 x )2
4x 2
4 so x =− or x =
5
2
3 1  1  199
− x −3
∴ f '(x ) = when x = − , y =f −  =
2 2  2 24
c f '(x ) = 12π x 2 217
when x = 5, y = f (5) = −
6
d f (x ) = (x + 1)2 = x 2 + 2 x + 1  1 199   217 
so  − ,  and  5, − 
∴ f '(x ) =2x + 2  2 24   6 
x3 + x − 3 3
e f (x) = = x2 + 1 −
x x Exercise 5F
2
= x + 1 − 3x −1
∴ f '(x ) =2 x + 3x −2
1 − 2x 1 2
1 y = = − = x −2 − 2 x −1
x2 x2 x
f f (x ) =(2 x − 1)(x + 3) 2

dy
= 2x 3 − x 2 + 6 x − 3 ∴ −2 x −3 + 2 x −2
=
dx
∴ f '(x ) = 6 x 2 − 2 x + 6  3
Therefore, the gradient at  2, − 
3 dy 3 12  4
4 a y =
1+ x x =
1 + x2 ∴ = x 1
dx 2 is − 2(2)−3 + 2(2)−2 =
4
7 1 −1
b y = 2
− =7 x −2 − x 2 So the gradient of the normal at
x x
this point is − 4
dy 1 −3  3 29
−14 x −3 + x 2
= ∴ y −  −  =−4(x − 2) ⇒ y =−4 x +
dx 2 4 4
 
1 1
c y =3 x + 4
x =x 3 + x 4
dy
2 −3x 2 + 4 x
=
dy 1 − 23 1 − 34 dx
∴ = x + x
dx 3 4 So the gradient at x = −1 is − 7
dy
=−7 ⇒ 3x 2 − 4 x − 7
Exercise 5E dx
dy = (3x − 7 ) ( x + 1) = 0
1 a = 2 x − 4 so the gradient at
dx 7
∴ x = or x =−1 (i.e. the tangent itself)
x = −1 is 2(−1) − 4 =−6 3
7 22
5
2x − 5 5 y  = −
b y= = 2 x 4 − = 2 x 4 − 5x −1 3 27
x x
22  7 419
dy ∴y + =−7  x −  ⇒ y =−7 x +
∴ = 8 x 3 + 5x −2 27  3 27
dx
so the gradient at (1, −3) is
8(1)3 + 5(1)−2 =
13

© Oxford University Press 2019 2

 Worked solutions

dy 1 Exercise 5G
3 = 1− 2
dx x 1 a =
y u5 where =
u 2x + 3
dy 1 1 dy dy du
dx
=−3 ⇒ 1 − 2 =−3 ⇒ x =±
x 2 = =
dx du dx
) (2 )
(5u= 4
10u 4
 1 5
= 10 (2 x + 3)
4
y ±  =±
 2 2
y = 1 − 2 x =(1 − 2 x ) 2
1

1 b
Gradient of normal is
3 1
y= u 2 where u= 1 − 2 x
 5 1  1 
∴ y − ± =   x −  ±  dy dy du  1 − 1 
 2 3  2  = =  u 2  ( −2 )
dx du dx  2 
1 5 1
⇒ y= x± m =−u
− 12
=− (1 − 2 x )
− 12
3 2 6
1 7 1 7 3
∴ y= x+ and y= x− c y =
−
−1
−3u 2
=
3 3 3 3 2
2x − 1
4 f '(x
= ) 6 x − 2k
u 2x 2 − 1
where=
f '(1) =6 − 2k =10 ⇒ k =−2
dy dy du  3 − 3 
5 f '(x )= 3x 2 − 2 x − 2= 0 = =  u 2  ( 4 x )
dx du dx  2 
2
( )
− 23
2 2  1 7 = 6 x 2x 2 − 1
⇒ x2 − x − = x −  =
3 3  3 9
3
1± 7  2
∴x =
d y = 2  x 2 −  = 2u3
 x
3
Coordinates are 2
u x2 −
where =
 1 + 7 7 − 14 7   1 − 7 7 + 14 7  x
 ,  ,  , 
 3 27   3 27 dy dy du
 = =
dx du dx
(6u )  2x + x2 
2
2
1
6 g(=
x) −nx − n −1
= x − n ∴ g '(x ) = 2
xn  2  1 
= 12  x 2 −   x + 2 
 x   x 
x(−nx − n −1 ) + nx − n
⇒ xg '(x ) + ng(x ) =
−nx − n + nx − n =
= 0 2 At
= x 0,
= y 6 so tangent passes

7 a f '(x )= 15ax 2 − 4bx + 4c through (0,6)

6 (1 − 2 x ) 3 =
1 1

b f '(x ) ≥ 0 ⇒ 15ax 2 − 4bx + 4c ≥ 0 y = 6u 3 where u =

1 − 2x

⇒ x2 −
4b
15a
x+
4c
15a
≥0
dy dy du
=
dx du dx
−2
=2u 3 ( ) ( −2) =−4u − 23

−4 (1 − 2 x )
− 23
 2b 
2
4b2 4c =
⇒ x −  − + ≥0
 15 a  225 a2
15 a so the gradient at
= x 0 is − 4
The LHS is valid for all real x and ∴ y − 6 =−4 ( x − 0 ) ⇒ y =−4 x + 6
2b
attains its minimum at x = so
15a
4b2 4c
− + ≥ 0 ⇒ b2 ≤ 15ac
225a2 15a
8 −20 x −1 + 1
f (x) = for x > 0
) 20 x −2 , g '(x=
∴ f '(x= ) 5 for x ∈ ¡
= '(x ) when 20 x −2 5
f '(x ) g=
⇒ x2 = 4⇒x = ±2
But x > 0 so x = 2 only

© Oxford University Press 2019 3

 Worked solutions

3 When =
x 1, =
y 1 so =
a 1+ b c y = x 2 − 3x = uv where u = x

a (1 + bx )
− 12 −1
y = au 2 where u =
= 1 + bx and =
v 2 − 3x

dy dy du  a − 23  ab − 23 dy du dv
= v +u
= =  − u  ( b) =
− u dx dx dx
dx du dx  2  2
ab  3 
=− (1 + bx ) 2
−3
= (1) 2 − 3x + x  − 
2  2 2 − 3x 
dy 3 4 − 9x
At (1,1) , = − =
dx 8 2 2 − 3x
ab b 3
(1 + b ) 2 = − 2a2 = − 8 ( )
−3 2
⇒− d y= (2 x + 1) x 2 − x + 1 = uv where
2
3a2
(x )
2
2
so b = u = 2 x + 1 and v = − x +1
4
3a2 3a2 dy du dv
⇒ a = 1+ ⇒ a2 = 1 + = v +u
4 4 dx dx dx
(2) ( x 2 − x + 1)
2
⇒ a = 2 ( a > 0 ) ∴ b = a2 − 1 = 3 =

4 + 2 (2 x + 1) (2 x − 1) ( x 2 − x + 1)
4 y= = 4u −3 where u= 3 − x
(3 − x ) 2 x (5x − 1) ( x 2 − x + 1)
3
=
dy dy du
=
dx du dx
= −12u −4 ( ) ( −1) =12u −4
e y = (2 − 3x ) x + 2 = uv

= 12 (3 − x )
−4
where u =
2 − 3x and v =
x +2
dy 3 dy du dv
so=at x 1,
= and therefore = v +u
dx 4 dx dx dx
4  1 
the normal has gradient − =( −3) x + 2 + (2 − 3x )  
3  2 x + 2 
1 4 4 11 −10 − 9 x
∴ y − =− ( x − 1) ⇒ y =− x + =
2 3 3 6 2 x +2
dy
y = x + 1 (3 − x ) = uv where
2
5 −9 x 2 + 2
= 2 a
dx
(3 − x )
2
dy u=
x + 1 and v =
Curve horizontal when =0
dx
dy du dv
= v +u
2 2 dx dx dx
So x =
± =
±
9 3  1 
=   (3 − x ) +
2
(
x + 1 −2 (3 − x ) )
2 x +1
dy ( x − 3) + 4 ( x − 3) ( x + 1)
2
Exercise 5H
∴ =
1 a =
y x 2 (2 x − = u x2
1) uv where = dx 2 x +1
and =v 2x − 1 =
( x − 3) ( x − 3 + 4(x + 1))
dy du dv 2 x +1
= v +u
dx dx dx
=
( x − 3) (5x + 1)
= (2 x ) (2 x − 1) + x 2 (2 ) 2 x +1
= 6 x 2 − 2 x = 2 x(3x − 1) b Using the result from part a,
y = (2 x − 3) ( x + 3) = uv where x −3 = 0 ⇒ x = 3
3
b
1
or 
 x + 1 =0 ⇒ x =−
5
( x + 3)
3
u=
2 x − 3 and v = 5
dy du dv
= v +u
dx dx dx
= (2 ) ( x + 3)
3
(
+ (2 x − 3) 3 ( x + 3)
2
)
( x + 3) ( 8 x − 3)
2
=

© Oxford University Press 2019 4

 Worked solutions

3 y =x (1 − 2 x )
−1
=uv where u =x 1 + 3x u
d y= = where u= 1 + 3x
x2 + 1 v
(1 − 2x )
−1
and v
=
v x2 + 1
and =
dy du dv dy vu '− uv '
= v +u =
dx dx dx dx v2
= (1) (1 − 2 x )
−1
(
+ x 2 (1 − 2 x )
−2
) = (1 −12x ) 2
=
(x 2
)
+ 1 (3) − (1 + 3x ) (2 x )

(x )
2
2
+1
so the gradient at (0,0) is 1 and
3 − 2 x − 3x 2
the normal therefore has gradient − 1 =
(x )
2
2
+1
∴ y =− x
−3x 2 + 4 x + 3
=2 f '(x ) = , f '(0) 3
( x + 1)
2
Exercise 5I
1 + 3x u so normal at this point has
1 a y= = where u= 1 + 3x
5−x v 1
gradient − and passes through (0, − 2)
and v= 5 − x , u ' = 3, v ' = −1 3
dy vu '− uv ' 1
= ∴ y =− x − 2
dx v2 3
(=5 − x ) (3) − (1 + 3x ) ( −1) 16 x3 + x2 + x + 1 u
3 f (x)
= =
(5 − x ) (5 − x )
2 2
x v

x u where u = x 3 + x 2 + x + 1 and v = x
b
= y = where
= u x
2−x v vu '− uv '
f '(x ) =
and v= 2 − x v2

1 =
( ) (
x 3x + 2 x + 1 − x 3 + x 2 + x + 1 (1)
2
)
u' = , v ' = −1 x 2
2 x
dy vu '− uv ' 2x 3 + x 2 − 1
= =
dx v2 x2
1
 1 
(2 − x ) 
2 x 
− ( x ) ( −1) f '(x ) = 1 ⇒ 2 x 3 + x 2 − 1 = x 2 ⇒ x 3 =
2
= 1
(2 − x )
2
∴x =3
2
2+x
=
2 (2 − x )
2
x Exercise 5J
1 + 2x u 1 a
c y= = where u= 1 + 2 x
1− x 2 v y =( x − 1) ( x + 3) =uv where
2

( x + 3)
2
and =
v 1 − x2 u=
x − 1 and v =
x dy du dv
u ' = 2, v ' = − = v +u
1 − x2 dx dx dx
dy vu '− uv '
= = (x + 3)2 + 2 ( x − 1) ( x + 3)
dx v2
 
=( x + 3) ( x + 3 + 2(x − 1))
x
1 − x 2 (2 ) − (1 + 2 x )  −  ( x 3) (3x + 1)
=+
2
 1− x 
=
1 − x2 b Most easily done using the product
x +2 (and chain) rule:
=
(1 − x ) y = ( x + 1) 1 − 2 x = uv
3
2 2

where u = x + 1 and v = 1 − 2x
dy du dv
= v +u
dx dx dx
x +1 3x
= 1 − 2x − =−
1 − 2x 1 − 2x

© Oxford University Press 2019 5

 Worked solutions

c Most easily done using the quotient 2 a f '(x ) = −3x 2

rule:
Increasing: nowhere
x +1 u
y= = where u= x + 1 Decreasing: ∀x ∈ ¡
x −1 v
and v= x − 1 b f '(x ) = 4 x
dy vu '− uv ' Increasing: x > 0
=
dx v2 Decreasing: x < 0
=
( x − 1) − ( x + 1) = − 2
1
( x − 1) ( x − 1) c f '(x ) = −
2 2

2 x −1
d Most easily done by chain rule
Increasing: nowhere
(quotient rule also valid)
(note the function is only valid here
( )
−1
y= 2 x 4 − 2 x + 1 = 2u −1 for x > 1)
Decreasing: x ∈ (1, ∞ )
4
where u = x − 2 x + 1
dy dy du  2 
== −
dx du dx  u 2 
3
 4x − 2 ( ) d f=
'(x )
1
−2
2 x
=
(
4 1 − 2x )
3

 1 
Increasing: x ∈  0,
( x − 2x + 1)
2
4 
 16 
(note the function is only valid here
1+ x u
2 f (x )= = where u= 1 + x for x > 0)
x −1 v
 1 
and v= x − 1 Decreasing: x ∈  ,∞
 16 

vu '− uv '
x −1
2 x
− 1+ x ( )
f '(x ) =
=
Exercise 5L
v2 ( x − 1)
2

1 a f '(x ) = 2 x , f '(x ) = 0 ⇒ x = 0
( )
2

x +2 x +1 x +1
=
− =
− f (x ) decreasing for x < 0 and
2 x ( x − 1) 2 x ( x − 1)
2 2
increasing for x > 0 so this is a
(3 + 1)
2
1 local minimum
f '(9) =
− =
−
2 (3) ( 9 − 1)
2
24 ∴ ( 0, −2 ) is a local minimum point

1 1 Graphically, this is a positive parabola

Tangent:y −
2
=−
24
( x − 9) so the turning point must be a local
7 x minimum (students should draw this)
⇒y = −
8 24 1
1 b f '(x )= 1 − , f '(x ) = 0 ⇒ x = 1
Normal:y − = 24 ( x − 9 ) x
2
431 f (x ) decreasing for 0 < x < 1
⇒ y= 24 x −
2 and increasing for x > 1 so
this is a local minimum
Exercise 5K ∴ (1, −1) is a local minimum point
1 a i x >0 Graphically, the graph is continuous,
ii Nowhere begins at ( 0, 0 ) and lim f ( x ) = ∞ so
x →∞
b i x ∈ (−∞, −1) U ( −1, 0 ) the turning point at (1, −1) must be a
ii x ∈ (0,1) U (1, ∞) local minimum point (and in fact this
case a global minimum).
c i x ∈ (−∞, −0.215) U (1.55, ∞ )
(Students should draw this.)
ii x ∈ ( −0.215,1.55)
c f '(x ) = 3x 2 − 12 x = 3x ( x − 4 )
d i x ∈ ( −∞, −1) U (1, ∞ )

ii x ∈ ( −1,1)

© Oxford University Press 2019 6

 Worked solutions

f '(x ) = 0 ⇒ x = 0 or x = 4 x3
2 f '(x ) = − 4x + 5
Consider the point ( 0,2 ) , 3
f (x ) increasing for x < 0 and x2 − 4
∴ f ''(x ) =
decreasing for 0 < x < 4 so this f ''(x ) =x 2 − 4 =0⇒x =±2
is a local maximum
f '(x) =
−2 (5 − 4 x )
− 12
3
Consider the point (4, −30)
f (x ) decreasing for 0 < x < 4 and −4 (5 − 4 x )
∴ f ''(x ) =
− 23

increasing for x > 4 so this is a

d2y
local minimum 4 = 2a2
dx 2
∴ ( 0,2 ) is a local maximum
(terms of order x and constants
and ( 4, −30 ) is local minimum
disapper upon differentiating twice)
Graphically, this is a positive cubic,
so the first turning point is a ∴ 2a2 =8⇒a=±2
maximum and the second point
a minimum Exercise 5N
(students should draw this) dy
1 a = 3x 2 − 1
dx
2 f '(x )= 3ax 2 + 4 x= x (3ax + 4 )
d2y
4 6 x ⇒ 0 at x =
= 0
f '(x ) = 0 when x = 0 or x = − dx 2
3a
Coordinates of point of inflexion are
It is given that the turning point,
away from x 0,
= = occurs at x 1
(0,0)
4 4 d2y
∴ 1 =− ⇒ a =− b = 6x > 0 ⇒ x > 0
3a 3 dx 2
3 p(0)
= d= 1 so d= 1 Function concave up on ]0, ∞[

p ( −1) =−a + b − c + 1 =−3   c

d2y
= 6x < 0 ⇒ x < 0
so  a − b + c =4 dx 2

c x (3ax + 2b ) + c
) 3ax 2 + 2bx + =
p '(x= Function concave down on ] − ∞, 0[

p '(0) = 3 ⇒ c = 3 ⇒ a − b = 1 dy
2 a = 4x 3 − 3
p '(−1)= 0 ⇒ − ( −3a + 2b ) + 3= 0 dx

2b d2y
⇒ a= −1 = 12 x 2 > 0
3 dx 2
2b There are no points of inflexion
∴ − 1 − b =1 ⇒ b =−6 ⇒ a =−5
3 d2y
b = 12 x 2 > 0
so a = −5, b = −6, c =
3, d =1 dx 2
dy Functions is concave up throughout its
4 = 3x 2 + 2ax = x (3x + 2a) = 0
dx domain
dy 2a c Function is never concave down
∴ = 0 when x = 0 or x =
−
dx 3 dy
3 a = 3x 2 − 12 x − 12
2a dx
∴− = 4 ⇒ a = −6
3 d2y
= 6 x − 12 = 0 at x = 2
y ( 4) =64 − 6 (16 ) + b =b − 32 =−11 dx 2
⇒b=
21 Coordinates of point of inflexion are
so the local maximum is at ( 0,21) (2, −38)
d2y
b = 6 x − 12 > 0 ⇒ x > 2
Exercise 5M dx 2
3 15 12 Function is concave up on ]2, ∞[
1 f '(x ) = 5x 2 ∴ f ''(x ) = x
2 d2y
c = 6 x − 12 < 0 ⇒ x < 2
dx 2

© Oxford University Press 2019 7

 Worked solutions

Function is concave down on ] − ∞,2[ d2y

b = 24 x 2 + 6 x > 0 ⇒ x > 0, x < −0.25
dy dx 2
4 a = 3x 2 + 2 x
dx Function is concave up for x > 0;
2
x < −0.25
dy 1
2
=6x + 2 =0 at x =− d2y
dx 3 c = 24 x 2 + 6 x < 0 ⇒ −0.25 < x < 0
dx 2
Coordinates of point of inflexion are
 1 25  Function is concave down for
− ,−  −0.25 < x < 0
 3 27 
dy
d2y 1 8 a =4 x 3 − 12 x 2 + 16
b = 6x + 2 > 0 ⇒ x > − dx
dx 2 3
d2y
1 = 12 x 2 − 24 x = 0 at x = 0,2
Function is concave up on ] − , ∞[ dx 2
3
Coordinates of point of inflexion are
d2y 1 (0, −16 ) , (2, 0)
c =2
6x + 2 < 0 ⇒ x < −
dx 3
d2y
1 b = 12 x 2 − 24 > 0 ⇒ x < 0, x > 2
Function is concave up on ] − ∞, − [ dx 2
3
Function is concave up when x < 0,
dy x>2
5 a = 12 x 2 − 4 x 3
dx
d2y
2 c = 12 x 2 − 24 < 0 ⇒ 0 < x < 2
dy dx 2
=24 x − 12 x 2 =0 at x =0,2
dx 2 Function is concave down when
Coordinates of point of inflexion are 0<x<2
(0, 0) , (2,16 ) 9 a f ' (=
x ) 3x 2 + 4 x
d2y 4
b = 24 x − 12 x 2 > 0 ⇒ 0 < x < 2 3x 2 + 4 x = 0 ⇒ x = 0, −
dx 2 3
Function is concave up for 0 < x < 2
f '' ( x
= ) 6x + 4
d2y
c = 24 x − 12 x 2 < 0 ⇒ 0 > x, x > 2 f '' ( 0 ) = 4
dx 2
 4
Function is concave down for f ''  −  =
−4
x < 0; x > 2  3
2
6 a
dy
= 3x 2 − 6 x + 3 f '' ( x ) =0⇒x =−
dx 3
 2 43 
d2y Non-horizontal inflexion at  − , 
= 6 x − 6 = 0 at x = 1  3 27 
dx 2
( x ) 3 ( x − 1)
2
Coordinates of point of inflexion are b f '=
(1, 0)
3 ( x − 1) = 0 ⇒ x = 1
2

d2y
b = 6x − 6 > 0 ⇒ x > 1 f '' ( x )= 6 ( x − 1)= 0 at x= 1
dx 2
f '' (1.1
= ) 0.6 > 0
Function is concave up on ]1, ∞[
f '' ( 0.9 ) =
−0.6 < 0
d2y
c = 6x − 6 < 0 ⇒ x < 1
dx 2 Second derivative = 0 at x = 1, there
is a change in concavity at x = 1.
Function is concave down on ] − ∞,1[
Therefore there is a horizontal inflexion
dy at (1, 0)
7 a = 8 x 3 + 3x 2
dx
d2y
=24 x 2 + 6 x =0 at x =0, −0.25
dx 2
Coordinates of point of inflexion are
( −0.25, 0.992) , (0,1)

© Oxford University Press 2019 8

 Worked solutions

c f '(x) =
−12 x 3 − 24 x 2 decreasing for x < 1
iv Concave upward for x ∈ ¡
−12 x 3 − 24 x 2 = 0 ⇒ x = 0, −2
4 c i f '(x) =12 x 3 + 12 x 2 =0⇒x =−1, 0
f '' ( x ) =−36 x 2 − 48 x =
0 at x =
0, −
3
f ''
= ( x ) 36 x 2 + 24x
129
f '' ( 0.1) = − f '' ( −1) =
60
25
111 f '' ( 0 ) = 0
f '' ( −0.1) =
25
Therefore local min at (−1, −3)
First and second derivatives = 0 at
2
x = 0, and there is a change in ii f '' ( x ) =36 x 2 + 24 x =0⇒x =− ,0
concavity at x = 0. 3
Therefore there is a horizontal inflexion Horizontal inflexion point at (0, −2)
at (0, 2) Non-horizontal inflexion point at
 2 70 
− ,− 
f ''(−2) =−48  3 27 

4 iii Increasing x > −1

Second derivative = 0 at x = − , and
3 Decreasing x < −1
there is a change in concavity at 2
4 iv Concave upward x < − or x > 0
x = − 3
3
2
Therefore there is a non-horizontal Concave downward − <x <0
3
 4 310 
point of inflexion at  − ,  Exercise 5O
 3 27 
1 a
1 −3
d f '(x) = x 2
2
First derivative has no roots, therefore
there are no points of inflexion.
10 a i f ' ( x ) = 3x 2 − 6 x − 6

3x 2 − 6 x − 6 =0 ⇒ x =−0.732,2.73
f ''(x
= ) 6x − 6
f '' ( −0.732 ) =
−10.392
f '' (2.73) = 10.38
Therefore local max at
(−0.732, 3.39) and local min at
(2.73, −17.4)
ii f '' ( x ) = 6 x − 6 = 0 ⇒ x = 1
Non-horizontal inflexion at (1, −7)
iii Increasing: x < −0.732 or x > 2.73
decreasing for −0.732 < x < 2.73
iv Concave downward x < 1 and
concave upward for x > 1 b
b i f ' ( x )= 2 ( x − 1) ⇒ x= 1

f '' ( x ) = 2
f (1) = 2
Therefore local min at (1, 0)
ii f '' ( x ) = 2 therefore there are no
inflexion points
iii Increasing for x > 1

© Oxford University Press 2019 9

 Worked solutions

c 2 a

Exercise 5Q
100
1 a L=
x
100
Exercise 5P b =
P 2x + assuming clarification to
x
1 a the question is made, as written in the
comments
100
c P '(x )= 2 −
x2
P '(x ) = 0 ⇒ x = 50 = 5 2 (x > 0)
This must be a minimum because
lim+ P(x ) = ∞ and lim P(x ) =
∞
x →0 x →∞

and this is the only turning point

(and the function is continuous)

So x = 5 2∴P 5 2 = ( )
2 5 2 +
100
5 2
( )
b
= 10 2 + 10 2
= 20 2 (measured in metres)
d

dy
2 = 600 + 30 x − 3x 2
dx
dy
=0 ⇒ x 2 − 10 x − 200
dx
=( x − 20 ) ( x + 10 ) =0

© Oxford University Press 2019 10

 Worked solutions

=∴ x 20 since x > 0 Exercise 5R

= 600 (20 ) + 15 (20 ) − (20 )= 10000
2 3
y(20) 1 a 3t 2 − 3, a(t ) =
v(t ) = 6t
Therefore, maximum profit is $10 000 b s(0) = −3, a ( 0 ) =
1, v(0) = 0
216 At this instant, the particle is 1 metre
3 a h=
s2 from the origin in the positive
864 direction, travelling towards the
b A s2 +
=
s origin at 3m/s, and is not accelerating
dA 864 c The particle is moving away from
c =2s − 2 =0
ds s
the origin at 9m/s and is
⇒ s3 432=
= so s 3
432 accelerating away from the origin 
4 The length of each side of the square is s at 12m/s2
Therefore the total length of wire used
d The change of sign of v ( t )
for the rectangle is 150 − 4s
Since the length is twice the length occurs =
at t 1 (t > 0)
of the width, e t >1
4s
the length of the rectangle is 50 − f s(0) = 1, s (1) = −1
3
2s so travels 2m in this period
and the width of the rectangle is 25 −
3
s (1) =
−1, s (3) =
19
so the total area enclosed by the
square and rectangle is so 20m travelled in this period
4s   2s  ∴ Altogether distance travelled is 22m

A =s2 +  50 −   25 − 
 3  3  2 a 1m
2
 2s  b s '(t ) = 12 − 3t 2 = 0 ⇒ t = 2
s2 + 2  25 −
= 
 3 
s (2 ) = 17 and this is clearly
 100s 4s2 
=s2 + 2  625 − +  a maximum so 17m
 3 9 
c v (=
t ) 12 − 3t 2
17s2 200s
= − + 1250
9 3 v ( 0 ) = 12, v (1) = 9, v (3) = −15
dA 34 200 300
= s− =0⇒s= d 16 + 17 =
33 so 33m
ds 9 3 17
5 Let the length of the shorter side of 3
3 s '(t ) = 15 − 10t ⇒ t =
2
the base be l , so the longer side
clearly attains maximum here as
measures 2l
the function is a negative parabola
Therefore the area of the base is 2l 2. 
2
Let the height be h 3 3 3 45
smax =s   =15   − 5   =
5 2 2 2 4
V = 2l 2h = 10 ⇒ h = 2
l
4 a s ( 0 ) = 10 so 10m
So the total cost is
2l 2 (10 ) + 2 (2l ) ( h ) ( 6 ) + 2 ( l ) ( h ) ( 6 )
C = b s ( t ) = 0 ⇒ t 2 − 5t − 10 = 0
180
= 20l 2 + 36lh = 20l 2 + 5 + 65
l ∴t
= ≈ 6.53 ( t > 0 )
1
2
dC 180 9 3

= 40l − 2 = 0 ⇒ l =   c v ( t )= s ' ( t )= 5 − 2t
dl l 2
 5 + 65 
2 1

 9 3  2 3 v −1
= 20   + 180  
∴ Cmin   = −8.06 ms
2 9  2 
= 164 (to nearest dollar) a ( t ) = v ' ( t ) = −2 ms−2

© Oxford University Press 2019 11

 Worked solutions

As both the velocity and acceleration dy

−10 (1 − 2 x ) (3x − 2 )
4 6
are negative, the diver is speeding up =
dx
as he/she hit the water.
+ 18 (1 − 2 x ) (3x − 2 )
5 5

5=
h0 0,
= v0 50 ∴ h ( t ) =50t − 4.9t 2

(1 − 2x ) (3x − 2)
4 5
=
50
h '(t ) = 50 − 9.8t = 0 ⇒ t =
9.8
( −10 (3x − 2) + 18 (1 − 2x ) )
2 (1 − 2 x ) (3x − 2 ) (19 − 33x )
4 5
(clearly maximum here) =
 50 
hmax h=
=   127.551 x −3 1 dy 1
 9.8  b y = = so = − 2
x ( x − 3) x dx x
so maximum height is 127.6m to 1d.p.
50 dy 1 − 12 4 − 23
t ground
= = 10.2041 c = x − x
4.9 dx 2 3
so hits ground after 10.2s to 1d.p. 5 a y = 0, x = ±1
6 a=t 0,=t 3,
= t 6,
= t 11 b Using the quotient rule,
b i Eastward is positive → 0 < t < 3; dy
=
(
x 2 − 1 − x (2 x ) )
6 < t < 11
( )
2
dx x2 − 1
ii Westward is negative → 3 < t < 6
2
x +1
c i t = 1.5 ii t = 4.5 =
− < 0 for all x ∈ ¡
( )
2

=d t 1.5
= and t 4.5 x2 − 1

e Speeding up: t ∈ (0,1.5) ; c

t ∈ (3, 4.5) ; t ∈ ( 6, 9 )

Slowing down: t ∈ (1.5,3) ;

t ∈ ( 4.5, 6 ) ; t ∈ ( 9,11)

Chapter Review
1 a y =2 b a=2
2 a

dy
6 = 3x 2 − 6 x − 9= 3 ( x − 3) ( x + 1)
dx
dy
∴ = 0⇒ x = −1 or x =3
dx
y ( −1) =−1 − 3 + 9 + 2 =7
y (3) =
27 − 27 − 27 + 2 =
−25
So y =
−25 and y =
7
7 Using the quotient rule,
dy 2 ( x − 1) − 2 x 2
5x + x 2 5x + x 2 = = −
( ) ( 1)
2 2
b lim
= lim
= 5 dx x − 1 x −
x →0 −
x x →0 +
x
∴ at (2, 4 ) the gradient is − 2
3 a y = 6, x = ±3 b y = 0, x = −3
4 a Using the product rule,

© Oxford University Press 2019 12

 Worked solutions

So the tangent at this point is 11 a f (x) =0⇒x =−1 b=y 0,

= x 0
y −4=−2 ( x − 2 ) ⇒ y =−2 x + 8 1 1 
c (x) 9  + 2 
f=
1  x x 
The gradient at (3,3) is − so
2
 1 2 
the gradient of the normal at this ⇒ f '(x ) = 9  − 2 − 3 
 x x 
point is 2
Therefore the normal at this point is ∴ f '(x ) =0⇒x = −2
1 x 9 9
y − 3 =− ( x − 3) ⇒ y =− + y = f (−2) = −
2 2 2 4
x 9 7  2 6 
∴ − + = −2 x + 8 ⇒ x = f=
''(x ) 9  3 + 4 
2 2 3  x x 
7 10  7 10   1 3 9
⇒y =−2   + 8 = ∴ P  , f ''(−2) = 9  − +  = >0
  4 8 8
3 3 3 3 
 9
8 x) 6 x 2 − 3
f '(= so  −2, −  is a local minimum
 4
f '(1) = 3
d For f(x) to be concave up f’’(x) > 0
So the normal to the curve at
 2 6 
1 9  3 + 4  > 0 ⇒ 2x + 6 > 0
this point has gradient −  x x 
3
x > −3
1 x 1
∴ y − 0 =− (x − 1) =− + e
3 3 3
dy
9 −3x 2 + 4 x
=
dx
dy
=−4 ⇒ 3x 2 − 4 x − 4 =0
dx
⇒ (3x + 2 ) ( x − 2 ) =
0
2
∴x =− or x = 2
3
 2 8 4 59
y  − = + 2   + 1=
 3  27 9
  27
y (2 ) =−8 + 8 + 1 =1
 2 59 
∴ − ,  and (2,1)
 3 27 
10 Using the quotient rule,

=
dy 2 x ( x + 1) − x
=
2
x 2 + 2x
=
x ( x + 2)
12 a
f (x ) =0 ⇒ x ( )
x − b =0
( x + 1) ( x + 1) ( x + 1)
2 2 2
dx 2
⇒ x 0 or
= = x b
dy b
= 0⇒x = 0 or x = −2 b f '(x )= 1 −
dx
2 x
Students may either use first derivative
or second derivative test here b2
i f '(x ) > 0 when x >
e.g. second derivative test: 4
b2
d2y
=
(
2 ( x + 1) − 2 x 2 + 2 x
3
) ( x + 1) ii f '(x ) < 0 when 0 < x <
4
dx 2 ( x + 1)
4

b
2 c f '' ( x ) = 3
= 4x 2
( x + 1)
3

i f '' ( x ) > 0 when b > 0

The second derivative is negative at
x =−2 and positive at x = 0 ii f '' ( x ) < 0 when b < 0
∴ ( −2, −4 ) is a local maximum
13 a v(=
t ) 49 − 4.9t
and ( 0, 0 ) is a local minimum
b v(t ) = 0 ⇒ t = 10

© Oxford University Press 2019 13

 Worked solutions

h(10) 49 (10 ) − 2.45 (10 )

2
=
= 490 − 245 = 245
So 245m
14 a v ( 0 ) = −2

b v ( t ) = 0 ⇒ (1 + t ) = 4t + 9
2

t 2 − 2t − 8 = ( t − 4 ) ( t + 2 ) = 0
So t = 4
2
c a ( t )= 1 −
4t + 9 18 a Letting x represent the number of $10
increases above $320. Then rental
2 3 income is
a ( 4) =
1− =
25 5
d Always speeding up since (320 + 10x ) (200 − 5x )
R(x ) = A1
acceleration is always positive R ' ( x ) =400 − 100 x =0 M1

15 a f ′ ( x ) = 4x 3 − 6 x 2 − 2x + 3 A1 x =4 A1
Which corresponds to $360 rent

b g '(x) =
( )
−4 x 2 + 1 − ( −4 x ) ⋅ 2 x
M1A1
R1
b i 200 − 5 × 4 =180 A1
(x )
2
2
+1
ii 360 × 180 =$64800 M1A1
4x 2 − 4
g '(x) = A1 19 a h ( 4 ) = 370
(x )
2
2
+1
and h (5) = 438 (3 s.f.) A1A1
c h ' ( x ) =1 ⋅ ( x − 7 ) + ( x + 2 ) ⋅ 1 M1
(t ) h′=
b v= (t ) 112 − 9.8t M1A1
h'(x
= ) 2x − 5 A1
c v (t ) =0 ⇒ 112 − 9.8t =0 M1
i ' ( x ) = 3 ⋅ 2 ⋅ (2 x + 3)
2
d M1
t = 11.4 (3 s.f .) A1
' ( x ) 6 (2 x + 3) A1
2
i=

16 a Graph 1 A1
as the gradient of the tangent at any d Double x-coordinate of maximum or
point is non-positive and therefore determine zero M1
different from 1. R1
22.8 (3 s.f .) A1
b Graph 2 A1
e
as y increases as x increases R1
c Graph 3 A1
as the other two functions are not
defined at infinity R1
d Graph 1 A1
as the function is decreasing. R1
17 a i 0 ≤ t ≤ 2 , 4.6 ≤ t ≤ 5 A1A1
and 8.5 ≤ t ≤ 10 A1
ii 2 ≤ t ≤ 4 and 5 ≤ t ≤ 7 A1A1
iii 4.6 ≤ t ≤ 8.5 A1
b f (t ) = 2t , g(t ) = 2
h(t ) =−3t + 14 , i(t ) = −1
1
f (t )
=
3
(2t − 17) A4 Shape A1
Domain 0 ≤ x ≤ 22.9 (3 sf) A1
c Up to two correct branches correct
A1; all branches correct A2; all branches Maximum 640 (3 sf) A1
correct and labels and scale also correct A3 f v (22.9 ) = −112 ms -1
M1A1

© Oxford University Press 2019 14

 Worked solutions

g a ( t ) = v ′ ( t ) = −9.8 M1A1 ( h′ o g ) ( x ) = h′ ( g ( x ) )
−1 −1
M1

which is constant A1AG x +2

= 2⋅ A1
f ′ ( 2 ) g ( 2 ) − f ( 2 ) g′ ( 2 ) x −1
 f ′
20 a i   (2 ) =
( ) ( h o g )′ ( x ) ≠ ( h′ o g ) ( x )
2
g
  g (2 ) −1 −1
AG
M1
 4
10 × 4 − 9 ×  − 
=  3 A1
42
52  13 
= =  = 3.25  A1
16  4 
ii ( g o f )′ (1) = g′ ( f (1) ) f ′ (1) M1
4 16
=− × 4 =− A1
3 3
b i False A1
as derivative changes sign. R1
b False A1
as the derivatives at these points
are not negative reciprocals.
R1
N (3) − N (1)
21 a = 1410 M1A1
3 −1
N (5 ) − N ( 4 )
= 2220 A1
5−4
the first period the number of cases
is increasing in average 1410 per
day; in the second period it
increases in average 2220 per day.
dN
b = 900t − 90t 2 M1A1
dt
c After 10 days (reaches 15 000 cases)
M1A1
d2N
d = 900 − 180t M1A1
dt 2
which gives the variation of the rate
at which the spread of the disease
spreads. R1
y +2
22 a x = M1
y −1

x ( y − 1) = y + 2 M1

xy − y = x + 2 A1
x +2
1
g −= (x) = g (x)
x −1
A1AG

( ) ( )( )
b h o g −1 ′ ( x ) = h′ g −1 ( x ) g −1 ′ ( x )
M1A1

x + 2  3   6 ( x + 2) 
= 2⋅ ⋅ −  = − 
x − 1  ( x − 1)   ( x − 1)3 
2
   
A1

© Oxford University Press 2019 15

 Worked solutions

6 Representing data: statistics for

univariate data
Skills check
2+3+4+5+6
1 a Mean
= = 4
5
13 + 9 + 7 + 12 + 15 + 19 + 2
=b Mean = 11
7
2 a The number that occurs most often is 5
b The numbers that occur most often are d The data is right or positively skewed
1 and 7 . The data is bimodal 2 a Continuous
3 a The median is the middle number, 6 b The frequency table is given here (note
b Arrange the data in order of size. difference between this one and the one
2, 3,5
  , 7, 8, 9 . in the solutions provided)

The median is in between 5 and 7 .

1
2
(5 + 7 ) =
6

Exercise 6A
1 a Discrete b
Continuous
c Continuous c The histogram is given here (note
d Discrete difference between this one and the one
2 a Stratified sampling in the solutions provided)
b Systematic sampling
c Simple random sampling
d Quota sampling
3 a Stratified sampling
b Stratified sampling
c Systematic sampling
d Simple random sampling
e Quota sampling

Exercise 6B d The data is right or positively skewed

1 a Continuous 3 a Continuous
b The frequency table is given here (note b Histogram from concise solutions
difference between this one and the one
in the solutions provided)

c The histogram is given here (note

difference between this one and the one
in the solutions provided)

© Oxford University Press 2019 Worked solutions 1

 Worked solutions

c The data is neither right nor left 2 a

skewed, it has normal distribution x f Mid value fm
4 a Frequency table from concise solutions (m)

b The data is left or negatively skewed 0 ≤ x ≤ 10 18 5 90

5 a The frequency table is given here (note 10 < x ≤ 20 14 15 210
difference between this one and the one
20 < x ≤ 30 12 25 300
in the solutions provided)
30 < x ≤ 40 9 35 315

40 < x ≤ 50 7 45 315

Σ f = 60 Σ fm = 1230

Σ fm 1230
=x = = 20.5
Σf 60
b
x f Mid value fm
(m)

0 ≤ x ≤ 12 4 6 24

12 < x ≤ 24 0 18 0

24 < x ≤ 36 8 30 240
b The data is left or negatively skewed 36 < x ≤ 48 15 42 630

48 < x ≤ 60 13 54 702
Exercise 6C 60 < x ≤ 72 66 462
7
1 a The number that occurs most often is
Σ f = 47 Σ fm = 2058
8
b The number that occurs most often is Σ fm 2058
=x = = 43.7872 ≈ 43.8
4 Σf 47
c The number that occurs most often c
is 13 x f Mid value fm
(m)
d Each number occurs only once, so there
is no mode 1 ≤ x ≤ 1.5 4 1.25 5

e The numbers that occur most often are 1.5 < x ≤ 2 6 1.75 10.5
2 and 4 . The data is bimodal 2 < x ≤ 2.5 7 2.25 15.75
2 a The shoe size with the highest 2.5 < x ≤ 3 7 2.75 19.25
frequency is 10
3 < x ≤ 3.5 5 3.25 16.25
b The modal mark range is 60 < y ≤ 80
Σf = 29 Σfm = 66.75
3 a i The mode is 3
Σfm 66.75
ii The modal range is 30 < x ≤ 35 =x = = 2.30172 ≈ 2.30
Σf 29
b i Discrete data, since the scale on the
3 Mean
x-axis is given as discrete values.
0 × 6 + 1 × 5 + 2 × 4 + 3 × 7 + 4 × 10 + 5 × 4
ii Continuous data, since there is a =
6 + 5 + 4 + 7 + 10 + 4
continuous scale of values on the x-
axis. 94
= = 2.6111 ≈ 2.6 cups of coffee
36
Exercise 6D 4 a Phil had
1 a The mean is 3.65 2 + 4 + 4 + 6 + 10 + 15 + 4 + 5
b The mean is 12.8056 = 50 tomato plants
c The mean is 3.35 b The modal number of tomatoes per
plant was 8
c Mean =
3 × 2 + 4 × 4 + 5 × 4 + 6 × 6 + 7 × 10 + 8 × 15 + 9 × 4 + 10 × 5
50

177
= = 7.08
25

© Oxford University Press 2019 2

 Worked solutions

5 The mean number of fish caught per day numbers, the mean is 4 , so
was 2+3+4+4+ x +y
0 × 1 + 1 × 5 + 2 × 4 + 3 × 2 + 4 × 3 + 5 × 5 + 6 × 3 + 7 × 2 + 8 × 3 + 9 × 1 + 10 × 2 4=
1+5 + 4 +2 +3+5+3+2 +3 +1+2 6
141 6 × 4 = 13 + x + y
= ≈ 4.55
31 24 − 13 =x + y
6 The mean amount received per day is
11= x + y
5 × 6 + 15 × 14 + 25 × 15 + 35 × 8 + 45 × 2
As x and y are positive integers less than
6 + 14 + 15 + 8 + 2
8 , the only possible solution is if x = 5
197 and y = 6 (or y = 5 and x = 6 ), so the
= = $21.89
9
numbers are 2,3, 4, 4,5, 6
7 a There are
12 The mean mass of the students is
7 + 12 + 10 + 9 + 7 + 6 + 6 + 3
52 × 8 + 44 × 12 236
= 60 families represented = = 47.2 kg
20 5
b The data is right or positively skewed
c The mode of the data is 2 children per Exercise 6E
family
1 a The median is the middle number, 18
d The mean number of children is
7 × 1 + 12 × 2 + 10 × 3 + 9 × 4 + 7 × 5 + 6 × 6 + 6 × 7 + 3 × 8 b The middle number lies between 18
60 18 + 19 37
and 19 , = = 18.5
39 2 2
= = 3.9
10
c Arranging the numbers in size order
8 a There are 40 + 60 + 80 + 30 + 10 1, 2,  4,5   , the middle number is 4
  ,5
= 220 people in the village d The numbers are already in size order
b The modal class is 40 < a ≤ 60 (reversed), so the middle number is the
c The mean age of the villagers is median, the middle number lies
40 × 10 + 60 × 30 + 80 × 50 + 30 × 70 + 10 × 90 3+4 7
between 3 and 4 , = = 3.5
220 2 2
460 e 2, 4,5
  ,5   0 . The middle
  , 6, 7, 7, 8, 8,1
= ≈ 41.8
11 number is between 6 and 7 ,
9 In the set of numbers, each appears only 6 + 7 13
= = 6.5
once, so therefore for 2 to be the mode, 2 2
a = 2 . Given that the mean is 5, we have f   , 5, 6, 8 . The median is 5
2, 3,5
1 + 2 + 2 + 4 + 5 + 6 + b + 8 + 10 ,
5= 2 Total number of days
9
= 2 + 4 + 3 + 7 + 11 + 18 + 6 + 2 = 53
9 38 + b , 45
5 ×= = 38 + b , =
b 45 − 38 , th th
b=7 Median  n + 1  53 + 1  th
=  =  =  27
= 9
 2   2 
10 Given that the mean of the numbers is 23,
we have to find x 3 a Mean
8 + x + 17 + (2 x + 3) + 45 =
2000000 × 1 + 1000 × 10 + 600 × 14 + 200 × 25
23 = 1 + 10 + 14 + 25
5
23 × 5 = 73 + 3x 2023400
= = $40468
115
= 73 + 3x 50

115 − 73 =
3x b The mode is the most common number,
200
42 = 3x
c The median number is the number in
42 th
x = ,  50 + 1 
3 the   = 25.5 position, that is
th

x = 14  2 
the number between 200 and 600 ,
11 Starting with 2 and 3 , we know that as 4
200 + 600
is the mode, it must occur at least twice, = 400
start by assuming that there are two 4 s 2
then x and y are the remaining two

© Oxford University Press 2019 3

 Worked solutions

Exercise 6F IQR
= Q3 − Q1 .
1 a The median is the middle number, 8 th th
 n + 1  11 + 1  rd
th th Q1 
= =
  =
 3= 25
 n + 1  11 + 1   4   4 
b Q1 
= =
  =

rd
3= 7
 4   4   3 ( n + 1) 
th
 3 (11 + 1) 
th
th
th th
Q
=3  =
  =
 9= 45
 3 ( n + 1)   3 (11 + 1)   4   4 
c Q3 =
=   
 4 4 IQR = Q3 − Q1 = 45 − 25 = 20
   
th
= 9= 12 5 Q1 is the median of the lower half of the

d IQR = Q3 − Q1 = 12 − 7 = 5 numbers, 2
Q3 is the median of the upper half of the
e Range = largest – smallest
numbers, it lies between 4 and 5 , 4.5
= 15 – 3 = 12
IQR = Q3 − Q1 = 4.5 − 2 = 2.5
2 In ascending order, the numbers are
th th
2,  4,  5,  5,  5,  6,  6,  7,  8, 9,10,  15  n + 1  12 + 1 
6 a i Median =
=  =  6.5th
a Median  2   2 
 n + 1
th
 12 + 1 
th
9+r
=  = = 6.5
= th
6 ⇒ =9.5
   2
 2   2 
9+r
b Q1 is the median of the lower half of 9.5 =
2
the numbers, 5
9.5 × 2= 9 + r
c Q3 is the median of the upper half of
19 − 9 =r
the numbers, it lies between 8 and 9 ,
r = 10
8.5
ii Q3 is the median of the upper half of
d IQR = Q3 − Q1 = 8.5 − 5 = 3.5
the numbers, it is between s and 13
e Range = largest − smallest = 15 − 2 = 13 s + 13
13 =
3 Sorting the number of sit-ups into 2
ascending order,
21 × 3 = s + 13
2, 
10, 1
 0, 1
 2, 1
 4, 1
 6, 1
 6,  
20,  
25,  
25, 
26 − 13 =
s
28,  30,  37,   40,   45,  50
s = 13
a Median
th th b The value of t can be found as follows
 n + 1  16 + 1 
= =  =  8.5th 10 =
5 + 6 + 7 + 7 + 9 + 9 + 10 + 10 + 13 + 13 + 13 + t ,
 2   2  12
20 + 25 10 ×=
12 102 + t
= = 22.5
2 120 − 102 =
t
b Q1 is the median of the lower half of t = 18
12 + 14
the numbers, = 13
2 Exercise 6G
Q3 is the median of the upper half of 1
30 + 37
the numbers, = 33.5
2
IQR = Q3 − Q1 = 33.5 − 13 = 20.5
c On 8 of the 16 days, Lincy did more 2 a The minimum time was 30.1
than 22.5 sit-ups.
b The maximum time was 35
d The ‘middle half’ of the number of sit-
ups Lincy did was between 13 and 33.5. c The median time was 32.5
e On 4 of the 16 days, Lincy did more d The IQR was 33.1 − 31.9 =
1.2
than 33.5 sit-ups.
4 Sorting the number of cars into ascending
order,
20,  20,  25,  30,  35,  35,  35,  35,   45,   45,  
50.

© Oxford University Press 2019 4

 Worked solutions

3 a c IQR = 13.6 − 8.2 = 5.4 minutes

d k = 15.6 minutes
2 a The median is 40 minutes
b IQR = 50 − 30 = 20
c 53
b Q3 + 1.5(IQR) 3 a
= 2067.5 + 1.5 × 1272.5
= 3976.25 < 6000
so it is an outlier
b
c

d The outlier was removed because it

distorted the analysis
4 a

c The median is 73 km
d IQR = 82 − 60 = 22 km
b The morning exam
c This means that there is a bigger e 3 cars
difference between the 25% and the 4 a
75% of the scores
5 a

c The data is right or positively skewed

6 1A, 2C, 3B

Exercise 6H
c The median is 420
1 a The longest time taken was 18 minutes
d IQR = 510 − 300 = 210
b The median is 11 minutes

© Oxford University Press 2019 5

 Worked solutions

e 80 students Σx
2 a x =
5 1C, 2B, 3A n
1×3 + 2× 8 + 3× 6 + 4 × 6 + 5×7
= = 3.2
Exercise 6I 3+8+6+6+7
2
Σx 4 + 6 + 7 + 7 + 5 + 1 + 2 + 3
Σx 2  Σx 
1 a =
x = −  σ2 =
n 8 n  n 
= 4.375 12 × 3 + 22 × 8 + 32 × 6 + 42 × 6 + 52 × 7
= − 3.22
3+8+6+6+7
2
Σx 2  Σx  = 12 − 10.24 = 1.76
σ2 = − 
n  n  σ
= σ 2 ≈ 1.33
4 + 6 + 7 + 72 + 52 + 12 + 22 + 32
2 2 2
Σx
− 4.3752 b x =
8 n
=23.625 − 19.1406 ≈ 4.48
1 × 5 + 3 × 12 + 5 × 16 + 7 × 22 + 9 × 27 + 11 × 30 + 13 × 18
=
σ
= σ 2 ≈ 2.12 5 + 12 + 16 + 22 + 27 + 30 + 18

≈ 8.32
Σx
b x = 2
n Σx 2  Σx 
σ2 = − 
n  n 
2 + 5 + 8 + 7 + 1 + 3 + 9 + 11 + 4 + 2
= 12 × 5 + 32 × 12 + 52 × 16 + 72 × 22 + 92 × 27 + 112 × 30 + 132 × 18
10 =
5 + 12 + 16 + 22 + 27 + 30 + 18
− 8.3232

= 5.2
2
= 80.385 − 69.273 = 11.111
Σx 2  Σx 
σ = 2
−  σ
= σ 2 3.33
=
n  n 
Σx
22 + 52 + 82 + 72 + 12 + 32 + 92 + 112 + 42 + 22 c x =
10
− 5.22 n
=37.4 − 37.04 ≈ 10.4 5 × 18 + 15 × 14 + 25 × 13 + 35 × 11 + 45 × 6
=
18 + 14 + 13 + 11 + 6
σ
= σ 2 ≈ 3.22
≈ 20.6
Σx −4 + −2 + 0 + 3 + −5
c x = = = −1.6 Σx 2  Σx 
2
n 5 σ2 = − 
2 n  n 
Σx 2  Σx 
σ2 =−  52 × 18 + 152 × 14 + 252 × 13 + 352 × 11 + 452 × 6
n  n  =
18 + 14 + 13 + 11 + 6
− 20.6452

(−4)2 + (−2)2 + 02 + 32 + (−5)2 = 602.419 − 426.223 = 176.197

− 5.22
5
σ
= σ 2 ≈ 13.3
= 10.8 − 2.56 = 8.24
Σx
σ
= σ 2 ≈ 2.87 3 a x =
n
Σx 1 + 2 + 3 + 4 + 5
d =
x = = 3 =
1 × 2 + 2 × 2 + 3 × 4 + 4 × 10 + 5 × 12 + 6 × 2 + 7 × 2 + 18 × 1
n 5 2 + 2 + 4 + 10 + 12 + 2 + 2 + 1
2
Σx 2  Σx  = 4.63
σ2 = −  2
n  n  Σx 2  Σx 
σ2 = − 
12 + 22 + 32 + 42 + 52 n  n 
= − 32
5 =
12 × 2 + 22 × 2 + 32 × 4 + 42 × 10 + 52 × 12 + 62 × 2 + 72 × 2 + 182 × 1
− 4.6292
2 + 2 + 4 + 10 + 12 + 2 + 2 + 1
= 11 − 9 = 2
= 28.571 − 21.424 = 7.148
σ
= σ 2 ≈ 1.41
σ
= σ 2 2.67
=
Σx 1 + 2 + 3 + 4 + 5 + 500
e =
x = ≈ 85.8 Σx
n 6 b x =
2 n
Σx 2  Σx 
σ2 = −  1 × 2 + 2 × 2 + 3 × 4 + 4 × 10 + 5 × 12 + 6 × 2 + 7 × 2
n  n  =
2 + 2 + 4 + 10 + 12 + 2 + 2
12 + 22 + 32 + 42 + 52 + 5002 = 4.24
= − 85.8332
6 2
Σx 2  Σx 
= 41675.833 − 7367.36 ≈ 34308 σ2 = − 
n  n 
σ
= σ 2 ≈ 185.2 12 × 2 + 22 × 2 + 32 × 4 + 42 × 10 + 52 × 12 + 62 × 2 + 72 × 2
= − 4.2352
2 + 2 + 4 + 10 + 12 + 2 + 2

© Oxford University Press 2019 6

 Worked solutions

= 19.882 − 17.938 = 1.945 Σx

2 a x =
σ
= σ
= 2
1.40 n
7 + 9 + 3 + 0 + 1 + 8 + 6 + 4 + 10 + 5 + 5
Σx = = 5.2727
4 x = 11
n 2
Σx 2  Σx 
=
93 + 86.2 + 80 + 64 + 60.6 + 50 + 50 + 47.3 + 46.6 + 46 σ2 = − 
10 n  n 
= 62.37 =
72 + 92 + 32 + 02 + 12 + 82 + 62 + 42 + 102 + 52 + 52
− 5.27272
2 11
Σx 2  Σx 
σ2 = −  = 36.909 − 27.802 = 9.11
n  n 
σ
= σ 2 3.02
=
932 + 86.22 + 802 + 642 + 60.62 + 502 + 502 + 47.32 + 46.62 + 462
− 62.372
10
Σx
b x =
= 4177.27 − 3890.02 = 287.248 n
σ
= σ 2 16.9
= 21 + 27 + 9 + 0 + 9 + 24 + 18 + 12 + 30 + 15 + 15
=
11
Σx
5 x =
n = 15.8182
2
Σx 2  Σx 
σ2 = − 
150 × 3 + 250 × 6 + 350 × 11 + 450 × 5 n  n 
= = 322
3 + 6 + 11 + =
5 212 + 272 + 92 + 02 + 92 + 242 + 182 + 122 + 302 + 152 + 152
− 15.81822
2
11
2
Σx  Σx 
σ2 = −  = 332.182 − 250.215 ; 82.0
n  n 
σ
= σ 2 9.054
=
1502 × 3 + 2502 × 6 + 3502 × 11 + 4502 × 5
= − 3222 c The mean is multiplied by 3, and since
3 + 6 + 11 + 5
the variance is multiplied by 9,
= 112100 − 103684 = 8416
standard deviation (which is square
σ
= σ 2 91.7
= root of variance) is multiplied by 3.
6 a 6 + 8 + 6 +3+1 =24 months 3 mean= 17.2 + 4= 21.2
b The modal range is 20 to 30 hours median = 17 + 4 = 21
standard deviation = 0.5
Σx
c x = 4 The mean, median and standard deviation
n
will double
15 × 6 + 25 × 8 + 35 × 6 + 45 × 3 + 55 × 1
= 5 The new variance is 92 x = 81x
6 + 8 + 6 +3+1
= 28.75
2 Chapter Review
Σx 2  Σx 
d σ2 = −  1 a mode = 1
n  n 
th
 10 + 1  4+2
b median =  =  5.
= 5th =3
152 × 6 + 252 × 8 + 352 × 6 + 452 × 3 + 552 × 1  2  2
= − 28.752
6 + 8 + 6 +3 +1
2 + 8 +1+5+ 0 + 4 + 4 +1+1+ 6
950 − 826.563 =
= 123.438 c mean =
10
σ
= σ 2 11.1
= 16
= = 3.2
5
Exercise 6J d range = 8 − 0 = 8
1+3+5+5+8
1 a mean = 4.4
= 9 × 420 + 3 × 740
5 2 = 500
12
median = 5
mode = 5 3 a mode = 3
th
5 + 7 + 9 + 9 + 12  50 + 1 
b mean
= = 8.4 b median =   = 25.5th = 3
5  2 
median = 9 c 0 × 4 + 1 × 8 + 2 × 10 + 3 × 20 + 4 × 4 + 5 × 3 + 6 × 1
mean =
mode = 9 50

c Adds 4 to mean, median and mode 5

= = 2.5
2

© Oxford University Press 2019 7

 Worked solutions

4 The mean will increase by 4 and the 11 mode = 4

standard deviation will stay the same; mean
mean = 21.9 , standard deviation = 1.1 2 × 3 + 3 × 4 + 4 × 10 + 5 × 3 + 6 × 2 + 7 × 2
=
736 3 + 4 + 10 + 3 + 2 + 2
5 a mean = = 32
23 = 4.125
th
736 + 24 + 15  24 + 1 
b mean = = 31 median =   = 12.5th = 4
23 + 2  2 
22 × 3 + 32 × 4 + 42 × 10 + 52 × 3 + 62 × 2 + 72 × 2
6 a The mean will increase by 10 and the σ2 =
3 + 4 + 10 + 3 + 2 + 2
− 4.1252

standard deviation will stay the same;

=18.875 − 17.0156 =1.8593
mean = 58 , standard deviation = 5
σ = 1.36
b The mean will increase by a factor of 10
and the variance will increase by a 12 a mean =
2.5 × 15 + 7.5 × 11 + 12.5 × 9 + 17.5 × 12 + 22.5 × 6
15 + 11 + 9 + 12 + 6
factor of 102; mean = 480 , ≈ 10.9
2
variance = 5 × 100 =
2500  53 + 1 
th

median =   = 27th = 12.5

7 a 40  2 
b 60 σ2 =
2.52 × 15 + 7.52 × 11 + 12.52 × 9 + 17.52 × 12 + 22.52 × 6
15 + 1 1 + 9 + 1 2 + 6
− 10.8962

c 50 = c − 40 ⇒ c = 50 + 40 = 90 = 166.627 − 118.728 = 47.8996

d IQR = 24 = 74 − d ⇒ d = 74 − 24 = 50 σ = 6.92
8 a 800 students b Because we are using the midpoint of
b 65 marks each range, as opposed to the actual
original data, which assumes that the
c IQR = 75 − 55 = 20 number of items is equally spread
d 100 students throughout the class interval.
e No, because there are 100 students 13 Given that the mean number of watches is
who scored more than 80 marks, this is 2.5, we have to find k
not 10% 0 × 11 + 1 × 7 + 2 × 6 + 3 × k + 4 × 8 + 5 × 10
,
2.5 =
f k = 40 11 + 7 + 6 + k + 8 + 10
2.5 × (42 + k ) = 101 + 3k
9 1B, 2C, 3A
105 + 2.5k =101 + 3k
Σx
10 a x = 105 − 101 =(3 − 2.5)k
n
=
15 + 12 + 22 + 30 + 25 + 7 + 19 + 33 + 19 + 41 + 53 + 12 + 3 + 8 + 6 + 17 4 = 0.5k
16
4
= 20.125 k =
2 0.5
Σx 2  Σx 
σ2 = −  k =8
n  n 
152 + 122 + 222 + 302 + 252 + 72 + 192 + 332 + 192 + 412 + 532 + 122 + 32 + 82 + 62 + 172
14 a 80 bats
=

b 50 grams
16
− 20.1252

= 579.375 − 405.016 = 174.359 5

c
= 0.0625
= 6.25%
σ
= σ
= 13.22 80
b Write the numbers in size order; d a = 10 , c = 80 − 75 = 5
3, 6, 7, 8, 12, 12, 15, 17, 19, 19, e b = 75 − 55 = 20
22, 25, 30, 33, 41, 53 f Σx
x =
n
then find Q1 as the median of the first
half of the list, 15 × 10 + 45 × 45 + 75 × 20 + 105 × 5
=
 8 + 1
th
8 + 12 10 + 45 + 20 + 5
=Q1   4.5th
== = 10 and = 52.5
 2  2 2
Σx 2  Σx 
find Q2 as the median of the second σ2 = − 
n  n 
half of the list,
th 152 × 10 + 452 × 45 + 752 × 20 + 1052 × 5
 8 + 1 th 25 + 30 = − 52.52
Q1 = 8 +  = 12.5 = 27.5
= 10 + 45 + 20 + 5
 2  2
=3262.5 − 2756.25 =506.25
, so IQR= 27.5 − 10= 17.5
σ
= σ 2 22.5
=

© Oxford University Press 2019 8

 Worked solutions

15 a 50 =3 + 11 + 16 + m + 8 1.5 × IQR =9
⇒ m = 50 − 38 = 12 19 – 9 = 10 M1
n = 14 + 16 = 30 19 is the (only) outlier A1

b x =
Σx 20 a
∑x =70 ⇒ ∑ x =700 A1
n 10
10 × 3 + 15 × 11 + 20 × 16 + 25 × 12 + 30 × 8 Let the new student’s mass be s.
=
3 + 11 + 16 + 12 + 8 ∑ x + s = 72 M1
= 21.1 11
2 700 + s = 792 A1
Σx 2  Σx 
c σ2 = −  So s = 92kg A1
n  n  b IQR = 10 A1
102 × 3 + 152 × 11 + 202 × 16 + 252 × 12 + 302 × 8 76 + 1.5 × IQR = 76 + 15 = 91 M1
= − 21.12
3 + 11 + 16 + 12 + 8 So new student’s mass of 92 is an
=477.5 − 445.21 =32.3 outlier R1
16 a Discrete 21 a 200 A1
b 35 A1
Σx c Using mid-points 5, 15, 25… as
b x =
n estimates for each interval M1
1 × 41 + 2 × 60 + 3 × 52 + 4 × 32 + 5 × 15 + 6 × 8 i Estimate for mean is 22.25 A2
=
41 + 60 + 52 + 32 + 15 + 8 ii Estimate for standard deviation is
11.6 (3sf) A2
≈ 2.73
d Median is approximately the 100th
2
Σx 2  Σx  piece of data which lies in the interval
c σ2 = − 
n  n  20 < h ≤ 30 . A1
12 × 41 + 22 × 60 + 32 × 52 + 42 × 32 + 52 × 15 + 62 × 8
Will be 15 pieces of data into this
− 2.7312
=
41 + 60 + 52 + 32 + 15 + 8 interval
9.25 − 7.4571 =
= 1.7929 15
Estimate is 20 + × 10 = 23 M1A1
50
σ
= σ 2 1.34
=
22 a Discrete A1
d 1 standard deviation above the mean is b 5 A1
2.731 + 1.339 = 4.07 , so 15 + 8 =
23 c i 4.79 (3sf) A2
families have more than one standard ii 1.62 (3sf) A2
deviation above the mean mobile d i 5 A1
devices ii 4 A1
17 a Discrete A1 iii 5.5 A1
b Continuous A1 e
c Continuous A1
d Discrete A1
18 a As the mode is 5 there must be at least
another 5.
R1
So we have 1, 3, 5, 5, 6 with another
number to be placed in order R1
The median will be the average of the
A1 general shape
3rd and 4th pieces of data. R1
For this to be 4.5 the missing piece of A1 median
data must be a 4. A1 quartiles
Thus a=5, b=4 A1 A1 f IQR=1.5
1 + 3 + 4 + 5 + 5 + 6 24 1.5 × 1.5 =2.25 (A1)
b =x = = 4
6 6 5.5 + 2.25 = 7.75
M1 A1 4 - 2.25 = 1.75 M1
19 a An outlier is further than 1.5 times the So the 2 (unhappy) candidates with
IQR below the lower quartile or above grade 1 are outliers A1
the upper quartile. A1
b i mode = 8 A1
ii median = 7 A1
iii lower quartile = 3 A1
iv upper quartile = 9 A1
c IQR = 6

© Oxford University Press 2019 9

 Worked solutions

23 a c
x Frequency Cumulative
frequency
0 10 10
1 7 17
2 11 28
3 13 41
4 15 56
5 15 71
6 12 83
7 10 93
8 4 97
9 2 99
10 1 100
A4 for 6 correct
A3 for 4 or 5 correct
A2 for 2 or 3 correct
A1 for 1 correct
b i 4
ii 2
iii 6 A1A1A1
c i 4.05 (3sf)

(2.4140...)
2
ii = 5.83 (3sf) A1(M1)A1 A1A1scales A3 points and curve
d No. It is bimodal at x= 4 and 5. 24 d i 85
A1R1 ii 73
iii 97 A1A1A1
24 a 80 < w ≤ 90 A1 M1 lines
b 25 a i 7.5
mass cumulative ii 6.125 A1A2
frequency b i 6
40 < w ≤ 50 5 ii 6.9 A1A2
c Sally’s had the greater median R1
50 < w ≤ 60 20 d Rob’s had the greater mean R1
60 < w ≤ 70 45 26 a

70 < w ≤ 80 75
80 < w ≤ 90 125
90 < w ≤ 100 160
100 < w ≤ 110 185
110 < w ≤ 120 200
A2 numbers A1 labelling

chart A1; scaleA2

b i 4
ii 4
iii 4 A1A1A1
c The values of the median and the mean
are the same due to the symmetry of
the bar chart. A1R1

© Oxford University Press 2019 10