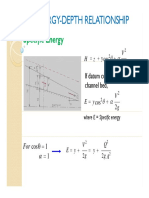
Lecture Note for Open Channel Hydraulics

Chapter 3

Critical Flow
3.1. Criterion for a critical state of flow
V
 The Froude number of critical flow is unity F  ,
gL

F = 1, Critical Flow Where V= mean velocity of flow

F< 1, Sub Critical Flow L= Characteristic length =
hydraulic radius (D) for open channel
F >1, Super critical Flow
 The specific Energy and specific force are minimum
 The discharge is maximum at critical flow for a given channel section
 The velocity head is equal to half the hydraulic depth at critical flow
o If this criterion is to be used in any problem, the following conditions must
be satisfied
 Flow parallel or gradually varied
 Channel of small slope
 Energy coefficient assumed to be unity
 The velocity of flow in a channel of small slope with uniform velocity
distribution is equal to the celerity of small gravity waves (C=gh) in shallow
water caused by local distribution.
 Flow at the critical state is unstable
o A minor change in specific energy at or close to critical state will cause a
major change in depth
Note:
 If the critical sate of flow have referred mainly to a particular section of channel,
known as the critical section
 If the critical sate of flow exists throughout the entire length of the channel or
over a reach of the channel the flow in the channel is a critical flow

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics
The section Factor for critical flow
The section factor for critical flow computation (Z) is the product of the water area and
the square root of the hydraulic depth.

A Z2
Z  A  A D  Z  A D D  2
2 2

T A
V2 D
For critical flow  , by substituting
2g 2

V2 D z2 V 2 A2 VA Q
   Z 2
  Z   Z  c
2g 2 2A2 g g g

Therefore, Qc  Z c g ------------------------------------------------------------ (3.1)

Where Qc represent the discharge that would make the depth y critical and know as the
critical discharge. When the energy coefficient is not assumed to be unity
g
Q c  Z c --------------------------------------------------- (3.2)

Eqns. 3.1 and 3.2 are very useful tool for the computation and analysis of critical
flow in open channel, when the discharge is give the equations will give the critical
section factor (Zc). and hence the critical Depth yc.
Section factor (Z) for different channel –section shape is give as :

2
Rectangular: Z  by 1 .5 Triangular: Z  my 2 .5
2
 y * ( b  my ) 1 .5
Trapezoidal: Z 
b  2 my
To simplify the computation of critical flow, dimensionless curves showing the
relation between the depth and the section factor Z have been prepared for different type
of channels sections. These self-explanatory curves will help to determine the depth y
for a given section factor Z and vice versa.

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Example 3.1 Compute the critical depth and velocity of the trapezoidal channel its
section given in the figure and carrying a discharge of 45m3/sec.

1.5

4.0m

Solution
Q 45
Given Qc  Z c g  Z c    14 . 37
b=4.0m g ( 9 . 81 )

y * (4  1.5 y 4 y  1.5 y 2 
m=1.5
Z
 y * (b  my)
1.5

 
1.5

 14.37  y  1.85m
Q= 45m3/sec b  2my 4  2 *1.5 * y 4  3y
c

2
A  (b  myc ) yc  ( 4  (1.5 * 1.85)) * 1.85  12.53m
Q 45
V    3.59m / s
A 12.53

First Hydraulic Exponent (M)

In many computations involving a wide range of depths in channel, such as in the
GVF computations, it is convenient to express the variation of Z with y in an exponential
form. The (Z-y) relationship Z 2  C1 y M is found to be very advantageous. In this
equation C1= a coefficient and M= an exponent called first hydraulic exponent. It is
found that generally M is a slowly –varying function of the aspect ratio for most of the
channel shapes.
y A dT 
An estimate of M can also be obtained by the relation M  3T 
A T dy 

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Example 3.2: Obtain the value of the first hydraulic exponent (M) for
a) Rectangular channel
b) Exponential channel where the area A=K1ya

Solution

a) Z  by 1.5  Z 2  b 2 y 3  C1  b 2 , M  3
dA
b) A  k1 y  T 
a
 k1ay a 1
dy

 A dT  y  
M 
y

A
3 T   
T dy  k 1 y  a 
3 k 1 ay a 1
 
k1 y a
k1 ay a 1

k1 a ( a  1) y a  2 
 
M 
1
k1 y a 1
 
3 k1 ay a 1  k1 ( a  1) y a 1  ( 3 a  ( a  1))  3 a  a  1  2 a  1

3.3 Transitions
The concepts of specific energy and critical energy are useful in the analysis of
transition problems. Transitions in rectangular channels are presented here. The
principles are equally applicable to channels of any shape and other types of transitions.

3.3.1 Channel with a Hump

a) Subcritical Flow
Consider a horizontal, frictionless rectangular channel of width B carrying
discharge Q at depth y1. Let the flow be subcritical. At a section 2 (Fig.3. 1) a smooth
hump of height Z is built on the floor. Since there are no energy losses between
sections 1 and 2, construction of a hump causes the specific energy at section to decrease
by Z. Thus the specific energies at sections 1 and 2 are,

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

V12
E1  y1 
2g
E 2  E1  Z

Figure: 3. 1. Channel transition with a hump

Since the flow is subcritical, the water surface will drop due to a decrease in the
specific energy. In Fig. (3.2), the water surface which was at P at section 1 will come
down to point R at section 2. The depth y2 will be given by,

V22 Q2
E2  y2   y2 
2g 2 gB 2 y 22

Figure 3.2 Specific energy diagram for Fig. (3.1)

It is easy to see from Fig. (3.2) that as the value of  Z is increased, the depth at
section 2, or y2 , will decrease. The minimum depth is reached when the point R
coincides with C, the critical depth. At this point the hump height will be maximum,
Zmax , y2 = yc = critical depth, and E2 = Ec = minimum energy for the flowing
discharge Q. The condition at Zmax is given by the relation,

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Q2
E 1   Z max  E 2  E c  y c 
2 gB 2 y c2

The question may arise as to what happens when Z >  Zmax. From Fig. (3.2) it is seen
that the flow is not possible with the given conditions (given discharge). The upstream
depth has to increase to cause and increase in the specific energy at section 1. If this
modified depth is represented by y1' ,

Q2
E 1'  y 1'  ( withE 1
'
 E 1 andy '
1  y1 )
2 gB 2 y 1' 2

At section 2 the flow will continue at the minimum specific energy level, i.e. at the
critical condition. At this condition, y2 = yc , and,
Q2
E 1'   Z max  E 2  E c  y c 
2 gB 2 y c2

Recollecting the various sequences, when 0 <  Z < Zmax the upstream water level
remains stationary at y1 while the depth of flow at section 2 decreases with Z reaching
a minimum value of yc at Z = Zmax . (Fig.3.2). with further increase in the value of
Z, (i.e., for Z >Zmax, y1will change to y1' while y2 will continue to remain yc). The

variation of y1 and y2 with Z in the subcritical regime can be clearly seen in Fig.3.3

Figure 3.3: Variation of y1 and y2 in subcritical flow over a hump

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Figure 3.4: Variation of y1 and y2 in supercritical flow over a hump

b) Supercritical Flow
If y1 is in the supercritical flow regime Fig (3.2) shows that the depth of flow
increases due to the reduction of specific energy. In Fig (3.2) point P` corresponds to y1
and point R` to depth at the section 2. Up to the critical depth, y2 increases to reach yc at
Z =  Zmax For  Z > Zmax, the depth over the hump y2 = yc will remain constant
and the max upstream depth y1 will change. It will decrease to have a higher specific
energy E1` by increasing velocity V1. The variation of the depths y1 and y2 with Z in
the supercritical flow is shown in Fig. (3.4).

Example 3.3: A rectangular channel has a width of 2.0 m and carries a discharge of
4.80m /sec with a depth of 1.60 m. At a certain cross-section a small, smooth hump with
a flat top and a height 0.10 m is proposed to be built.
a). Calculate the likely change in the water surface. Neglect the energy loss.
b). If the height of the hump is 0.50 m, estimate the water surface elevation on the
hump and at a section upstream of the hump.

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Solution:
Let the suffixes 1 and 2 refer to the upstream and downstream sections respectively as
shown in the figure
Q 4.8 q 2.40
q   2.40m3 / sec/m V1    1.50m / sec
B 2.0 y 1.60
V12 1.52
  0.115m
2g 2 * 9.81

V1 1.5
Fr1    0.38 , it show the upstream flow is subcritical and hump will
gy1 9.81 * 1.60

cause a drop in the water surface elevation. E1  1.60  0.115  1.715m

At section 2
E 2  E 1   Z  1 . 715  0 . 1  1 . 615 m 
V 22 2 . 40 2
E2  y2   1 . 615  y 2   y 2  1 . 48 ,
2g 9 . 81  2 y 22 The drop at water surface
1/3
q 2
 2 . 40 2 
yc  3     0 . 837 m
g  9 . 81 
Ec  1 . 5 y c  1 . 5 * 0 . 837  1 . 26 m

elevation is y  1.60  1.48  0.02m

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

b). If z=0.5
E2  E1  Z  1.715  0.5  1.215
Ec 2  1.5 yc  1.5 * 0.837  1.26 m

The minimum specific energy required at section 2 is greater than E2, (Ec2=1.26
>E2=1.215), the available specific energy at that section . Hence , the depth at section 2 will
be at the critical depth and E2=Ec2=1.26m. The upstream depth y1 will increase to a depth
y1 such that the new specific energy at the upstream section 1 is
V1'2 0.294
E1'  Ec 2  Z  y1'   Ec 2  Z  y1'  ' 2  1.76
2g y1

Solving by trial and error and selecting the positive root gives y1’ >y2, y1’ =1.648m

Example 3.4: Water flow in a wide channel approaches a 10 cm high hump at 1.50 m/sec
velocity and a depth of 1 m. Estimate
a) The water depth y2over the hump and
b) The hump height that will cause the crest flow to be critical.

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Solution
a). Froude number at upstream of the hump is
V1 1.5
Fr1    0.48  1( subcritica l )
gy1 9.81 * 1

V12 1.50 2
E1   y1   1.0  1.115m
2g 19.62
E 2  E1  Z  1.115  0.1  1.015m

q= V1y1=V2y2  V2= V1y1/y2

V 22 V 2y2
E2  y2   y 2  1 12
2g 2 gy 2
V12 y12
y 23  E 2 y 22   0  y 23  1.015 y 22  0 .115  0
2g

There are three roots y=0.859m, 0.451m and -0.296m. Since the third (negative) solution is
physically impossible and the second (smaller) one is for supercritical condition, they are
rejected for this subcritical hump. Thus the depth (y2) = 0.859m.

The water surface level dropped by

h= y1-y2-Z = 1-0.859-0.1=0.04m

b). For critical flow in a wide channel

q= vy=1.5*1=1.5m3/sec/m
Emin = Ec= 1.5(q2/g)1/3=1.5*(1.52/9.81)1/3=0.918m

Therefore the maximum height of the hump for frictionless flow over the hump is
Zmax = E1-Emin = 1.115-0.918=0.197m

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

3.3.2 Transition with a Change in Width

a) Subcritical Flow in a Width Constriction

Consider a frictionless horizontal channel of width B1 carrying a discharge Q at a
depth y1 as in Fig. (3.5). At a section 2 channel width has been constricted to B2 by a
smooth transition. Since there are no losses involved and since the bed elevations at sections
1 and 2 are the same, the specific energy at section1 is equal to the specific energy at
section2.

V 12 Q2
E 1  y1   y1 
2g 2 gB 12 y 12

V 22 Q2
E2  y2   y2 
2g 2 gB 22 y 22

Figure 3.5 Transition with width constriction

It is convenient to analyze the flow in terms of the discharge intensity q = Q/B. At

section 1, q1 = Q/B1 and at section 2, q2 = Q/B. since B2 < B1, q2 > q1. In the specific energy
diagram (Fig.3.6) drawn with the discharge intensity, point P on the curve q1 corresponds to
depth y1 and specific energy E1. Since at section 2, E2 = E1 and q = q2, point P will move
vertically downward to point R on the curve q2 to reach the depth y2.

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Thus, in subcritical flow the depth is y2 < y1. If B2 is made smaller, then q2 will
increase and y2 will decrease. The limit of the contracted width B2 = B2min is reached when
corresponding to E1, the discharge intensity q2 = q2max, i.e. the maximum discharge intensity
for a given specific energy (critical flow condition) will prevail.

Figure 3.6: Specific energy diagram for Fig. (3.5)

At the minimum width, y2=ycm= Critical depth

Q2
E 1  E C min  y cm 
2 g ( B 2 min ) 2 y cm
2

2
For a rectangular channel at critical flow y c  Ec
3
Since E1= Ecmin

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

2 2
y 2  y cm  E C min  E 1
3 3
1 / 3
 Q 2  Q 2
y c   2
  B 2 min  3
 B 2 min g  gy cm

3
Q 2
 3  27 Q 2
B 2 min  X    3
g  2 E 1  8 gE 1

If B2 < B2min, the discharge intensity q2 will be larger than qmax, the maximum
discharge intensity consistent E1. The flow will not, therefore, be possible with the given
upstream conditions. The upstream depth will have to increase to y1’. The new specific
energy which is given by:
Q2
E1'  y1' 
2 g ( B12 y1' 2 )

will be formed which will be sufficient to cause critical flow at section2. It may be noted
that the new critical depth at section 2 for a rectangular channel is,

1/3 1/ 3
 Q2   q2 
yc2   2    
B g
 2   g 
V c22
Ec2  yc2   1 .5 y c 2
2g

Since B2 < B2min , yc2 will be larger than ycm , yc2 > ycm . Thus even though critical flow
prevails for all B2 < B2min, the depth section 2 is not constant as in the hump case but
increases as y1`and hence E1` rises. The variation of y1, y2 and E with B2 /B1 is shown
schematically in Fig.3.7.

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Figure 3.7 Variation of y1 and y2 in subcritical flow in a width constriction

b). Supercritical Flow in a Width Constriction

If the upstream depth y1 is in the supercritical flow regime, a reduction of the flow
width and an increase in the discharge intensity causes a rise in depth y2. In fig. (3.6), point
P` corresponds to y1 and point R` to y2 . As the width B2 is decreased, R` moves up till it
becomes critical at B2 = B2min. Any further reduction in B2 causes the upstream depth to
decrease to y1` so that E1 rises to E1`. At section2, critical depth yc` corresponding to the
new specific energy E1` will prevail. The variation of y1, y2 and E with B2 /B1 in
supercritical flow regime is indicated in Fig. (5.21).

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Figure 3.8: Variation of y1 and y2 in supercritical flow in a width constriction

3.3.3 Choking
In the case of a channel with a hump, and also in the case of a width constriction, it
is observed that the upstream water surface elevation is not affected by the conditions at
section 2 till a critical stage is first achieved. Thus in the case of a hump for all  Z ≤ Zmax
, the upstream water depth is constant and for all Z > Zmax the upstream depth is
different from y1. Similarly, in the case of the width constriction, for B2 ≥ B2min, the
upstream depth y1 is constant; while for all B2 < B2min, the upstream depth undergoes a
change. This onset of critical condition at section 2 is a prerequisite to choking. Thus all
cases with  Z > Zmax or B2 < B2min are known as choked conditions . Obviously, choked
conditions are undesirable and need to be watched in the design of culverts and other
surface drainage features involving channel transitions.

By Belete B. AAiT Department of Civil Engineering

October 2010
 Lecture Note for Open Channel Hydraulics

Example 3.5: A rectangular channel is 3.50 m wide conveys a discharge of 15.0 m /sec at
a depth of 2.0 m. It is proposed to reduce the width of the channel at a hydraulic structure.
Assuming the transition to be horizontal and the flow to be frictionless determine the water
surface elevations upstream and downstream of the constriction when the constricted width
is
a) 2.50 m, and
b) 2.20 m.

3.3.4. General Transition

A transition in general form may have a change of channel shape, provision of a
hump or a depression, contraction or expansion of channel width, in any combination. In
addition, there may be various degrees of loss of energy at various components. However,
the basic dependence of the depths of flow on the channel geometry and specific energy of
flow will remain the same. Many complicated transition situations can be analyzed by using
the principles of specific energy and critical depth.

In subcritical flow transitions the emphasis is essentially to provide smooth and

gradual changes in the boundary to prevent flow separation and consequent energy losses.
The transitions in supercritical flow are different and involve suppression of shock waves
related disturbances.

Example 3.6: A discharge of 16.0 m /sec flows with a depth of 2.0 m in a rectangular
channel 4.0 m wide. At a downstream section the width is reduced to 3.50 m and the
channel bed is raised by Z. Analyze the water surface elevations in the transitions when
a) Z = 0.20 m and
b) Z = 0.35 m.

By Belete B. AAiT Department of Civil Engineering

October 2010