College of Engineering, Architecture and Technology

Name: ____________________________________Course & Year: ______________

Module 9 : Distributed Loads and Hydrostatics Forces: Cables
Course Title : Statics of Rigid Bodies
Course Number : MECH 211
Course Description : The course deals with the forces acting on non-moving
bodies. It covers concurrent and non-concurrent forces,
operation with the free body concepts, equilibrium of
coplanar and non-coplanar systems, friction forces,
centroids and moment of inertia.
Total Learning Time : 4 units (4 hours lecture per week)
Pre-requisites : Physics for Engineers, Calculus 2 – Integral Calculus
(if there’s any)

ENGR. EDMIL JHON B. ARIQUES 1

 College of Engineering, Architecture and Technology
Discussion:
Cables under Distributed Loads
Flexible cables are used in numerous engineering applications. Common examples are
power transmission lines and suspension bridges. The term flexible means that the cables
are incapable of developing internal forces other than tension. In earlier chapters we treated
cables as two-force members; that is, the weights of the cables were neglected, and the
loading consisted of end forces only. Here we consider the effects of distributed forces,
such as the weight of the cable or the weight of a structure that is suspended from the cable.
Concentrated loads are covered in the next article.
Figure below shows a cable that is suspended from its endpoints A and B. In order
to support the distributed loading of intensity w, the cable must assume a curved shape. It
turns out that the equation describing this shape is simplified if we place the origin of the
xy-coordinate system at the lowest point O of the cable. We let s be the distance measured
along the cable from O. The shape of the cable and the location of point O are generally
unknown at the beginning of the analysis.

From the Free Body Diagram

+↑ ∑ 𝐅𝐲 = 𝟎
T sin θ − W = 0
𝐓 𝐬𝐢𝐧 𝛉 = 𝐖
∑
+→ 𝐅𝐱 = 𝟎
T cos θ − W = 0
𝐓 𝐜𝐨𝐬 𝛉 = 𝐖
𝐖
𝐭𝐚𝐧 𝛉 = 𝐓 𝐓 = √(𝐓𝐎 )𝟐 + 𝐖
𝐎
Where:
T = Tensile force at C
TO = Tensile force at O

ENGR. EDMIL JHON B. ARIQUES 2

 W = Resultant of the distributed loading
θ = slope angle of the cable at C

Parabolic Cables
Here we analyze the special case in which the loading is distributed uniformly along
the horizontal; that is, 𝑤(𝑥 ) = 𝑤𝑜 where 𝑤𝑜 constant load intensity. This case arises, for
example, in the main cables of a suspension bridge see fig. a. where 𝑤𝑜 represents the
weight of the roadway per unit length. It is assumed that the roadway is connected to the
main cables by a large number of vertical cables and that the weights of all cables are
negligible compared to the weight of the roadway.

θ and T as functions of x and TO

From Fig, b where W = wO x
𝐰𝐎 𝐱
𝐭𝐚𝐧 𝛉 = 𝐓 = √𝐓𝐎 𝟐 + 𝐰𝐎 𝐱 𝟐
𝐓𝐎
Y as a function of x and TO
dy
Since tan θ = = slope
dx
dy wO x
=
dx TO
Integrating,
w x
∫ dy = ∫ TO dx
O
wO
∫ dy = TO
∫ xdx
wO x2
y= ( )
TO 2
𝐰𝐎 𝐱 𝟐
𝐲= 𝟐𝐓𝐎
S as a function of x and TO
dy 2
ds = √dx 2 + dy2 = √1 + (dx) dx
dy wO x
Substituting = and integrating, we obtain
dx TO
𝒙
wOx 𝟐
𝒔(𝒙) = ∫ √𝟏 + ( ) 𝒅𝒙
𝟎 TO

ENGR. EDMIL JHON B. ARIQUES 3

 𝒙 w x 𝟐 𝟏 T w x w x 𝟐
𝒔(𝒙) = 𝟐 √𝟏 + ( TO ) + 𝟐 (wO ) 𝐥𝐧 [ TO + √𝟏 + ( TO ) ]
O O O O

Catenary Cable
Consider a homogeneous cable that carries no load except its own weight. In this
case, the loading is uniformly distributed along the length of the cable; that is, 𝑤(𝑠) =
𝑤𝑂 , where 𝑤𝑂 is the weight of the cable per unit length, and the distance s is measured
along the cable. Therefore, the resultant of the loading shown in fig. b. is 𝑊 = 𝑤𝑜 𝑠.
𝜽 and T as functions of s and 𝑇𝑂
𝐰𝐨 𝐬
tan 𝛉 = 𝐓 = √𝐓𝐎 𝟐 + (𝐰𝐎 𝐬)𝟐
𝐓𝐎
S as a function of x and 𝐓𝐎
From equation ds = √dx 2 + dy 2
𝑑𝑦 2 𝑑𝑠 2
( ) =( ) −1
𝑑𝑥 𝑑𝑥
𝑑𝑦 𝐰𝐨 𝐬
From 𝑑𝑥 = tan 𝜃 = 𝐓𝐎
solving for dx yields,
𝑑𝑠
𝑑𝑥 =
2
√1+(𝐰𝐨𝐬)
𝐓𝐎

𝑠 𝑇 𝐰 𝐬 𝐰 𝐬 2
𝑥 (𝑠) = ∫0 𝑑𝑥 = 𝑤𝑂 ln [ 𝐓𝐨 + 1 + ( 𝐓𝐨 ) ]
𝑂 𝐎 𝐎
Solving this equation for s gives
𝑇 𝑤 𝑥
𝑠(𝑥 ) = 𝑤𝑂 sinh 𝑇𝑜
𝑂 𝑂
Y as a functions of x and 𝑇𝑂
𝐰 𝐱
𝑑𝑦 = tan 𝜃𝑑𝑥 = sinh 𝐓𝐨 𝒅𝒙
𝐎
Which gives
𝑥 𝑇 𝐰 𝐱
𝑦(𝑥 ) = ∫0 𝑑𝑦 = 𝑤𝑂 (cosh 𝐓𝐨 − 𝟏)
𝑜 𝐎
T as a function of x and 𝑇𝑂
𝐰 𝐱
𝑇 = 𝑇𝑂 cosh 𝐓𝐨
𝐎

Cables under Concentrated Loads

If the weight of the cable is negligible compared to the applied loads, then each
segment of the cable is a two-force member and the shape of the cable consists of a series
of straight lines. The analysis of a cable loaded in this manner is similar to truss analysis,
except that with cables the locations of the joints (i.e., points where the loads are applied)
are sometimes unknown.

ENGR. EDMIL JHON B. ARIQUES 4

 Where:
s = segment length
L = horizontal spacing of the loads
θ = angle between a segment and the horizontal
h = vertical position of the joint
i = arbitrary joint
The equilibrium equations for joint i in Fig. 6(b) are
+→ ∑ Fx = 0
Ti+1 cos θi+1 − Ti cos θi = 0
+↑ ∑ Fy = 0
Ti+1 sin θi+1 − Ti sin θi − Wi = 0
We see that the horizontal component Ti cos θi is the same for each segment.
Ti cos θi = TO i = 1,2, … … . n
T
Ti = O
cos θi
TO TO
(sin θi+1 ) − sin θi − Wi = 0
cos θi +1 cos θi
TO (tan θi+1 ) − TO (tan θi ) = Wi i = 1,2, … … . n − 1

Horizontal Spacings of the loads are given

h = ∑ni=1 L1 tan θi
Lengths of the segments are given
h = ∑ni=1 s1 sin θi
L = ∑ni=1 s1 cos θi

ENGR. EDMIL JHON B. ARIQUES 5

Exercises/ Drills:
Problems 1-2 Cables under Distributed Loads
1. The 36-m cable shown in Fig. (a) weighs 1.5 kN/m. Determine the sag H and the
maximum tension in the cable.

Solution:
FBD

For sag H
TO wo x
y=H= (cosh − 1)
wo TO
T 𝐰𝐨 𝐱
H = wO (cosh − 𝟏) ⟶ working equation
o 𝐓𝐎
For TO
T 𝐰𝐨 𝐱
s = wO sinh
o 𝐓𝐎
TO 𝟏.𝟓(𝟏.𝟓)
18 = sinh
1.5 𝐓𝐎
TO = 21.13 kN
TO 𝐰𝐨 𝐱 21.13 𝟏. 𝟓(𝟏. 𝟓)
𝐇= (cosh − 𝟏) = (cosh ) = 34.3 kN
wo 𝐓𝐎 1.5 𝟐𝟏. 𝟏𝟑

ENGR. EDMIL JHON B. ARIQUES 6

 lb
2. Figure (a) shows a cable that carries the uniformly distributed load wo = 80 ft , where
the distance is measured along the horizontal Determine the shortest cable for which
the cable tension does not exceed 10 000 lb, and find the corresponding vertical
distance H.

Solution:

FBD

+↺ ∑ MA = 0
(10000 sin θB)(200) − 10000 cos θB (40) − 16,000(100) = 0
sin θB − 0.2 cos θB − 0.8 = 0
θB = 62.98°
FBD of Line Segment OB

ENGR. EDMIL JHON B. ARIQUES 7

 ∑ Fx = 0
TO = TB cos θB = 10,000 cos 62.98° = 4543 lb
∑ Fy = 0
TB sin θB − 80LB = 0
10,000 sin 62.98° = 80LB
LB = 111.35 ft
LA = 200 − 111.35 = 88.65 ft
+↺ ∑ MO = 0
LB
TB sin θB (LB) − TB cos θB(H) − 80LB =0
2
(111.35)2
10,000 sin 62.98° (111.35 ) − 10,000 cos 62.98°(H) − 80 =0
2
H = 109.2 ft
For the Line Segment AO

x wOx 2 1 TO wOx wO x 2
s ( x) = √1 + ( ) + ( ) ln [ + √1 + ( ) ]
2 TO 2 wO TO TO
lb
Where: x = −LA = −88.65 ft, wO = 80 ft , and TO = 4543 lb
wO x 80(−88.65)
= 4543 = −1.5611
TO
−88.65 1 4543
s(−LA ) = √1 + (−1.5611)2 + ( )
2 2 80
ln [−1.5611 + √1 + (−1.5611)2 ]
s(−LA ) = −117.0 ft
Or SA = 117.0 ft

For the Line Segment OB

x wOx 2 1 TO wOx wO x 2
s ( x) = √1 + ( ) + ( ) ln [ + √1 + ( ) ]
2 TO 2 wO TO TO
lb
Where: x = −LA = 111.35 ft, wO = 80 ft , and TO = 4543 lb
wO x 80(111.35)
= 4543 = 1.96
TO
111.35 1 4543
s(−LB) = √1 + (1.96)2 + ( )
2 2 80
ln [1.96 + √1 + (1.96)2 ]
s(−LB) = 163 ft
Or SB = 163 ft
Total Length of the cable
SA + SB = 117 ft + 163 ft = 280 ft

ENGR. EDMIL JHON B. ARIQUES 8

Part 3-4 Cables under Concentrated Loads
3. For the cable loaded as shown in Fig. (a), determine the angles 𝛽1 and 𝛽2 , the force
in each segment, and the length of the cable.

Solution:
FBD

+↺ ∑ MA = 0
T3 sin 35° (24) + T3 cos 35°(6) − 1600(6) − 2000(17) = 0
T3 = 2334 N
For Horizontal Component
TO = T3 cos θ3 = 2334 cos 35° = 1912 N
For β2
From TO(tan θi+1 − tan θi ) = Wi for Joint 2 where i = 2
TO(tan θ3 − tan θ2 ) = W2
1912(tan 35° − tan θ2 ) = 2000
θ2 = −19.08° or 𝛃𝟐 = 𝟏𝟗. 𝟎𝟖°
From TO tan θi+1 − tan θi ) = Wi for Joint 1 where i = 1
(
TO(tan θ2 − tan θ1 ) = W1
1912[tan(−19.08°) − tan θ1 ] = 1600
θ1 = −49.78° or 𝛃𝟏 = 𝟒𝟗. 𝟕𝟖°
For Tensions in each segment,
TO = T1 cos θ1 ; 1912 = T1 cos(−49.78°)

ENGR. EDMIL JHON B. ARIQUES 9

 T1 = 2961 N
TO = T2 cos θ2 ; 1912 = T2 cos(−19.08°)
T2 = 2023 N
For Total Length of the Cable
s = s1 + s2 + s3
From FBD
L L L
cos β1 = s 1 ; cos β2 = s 2 ; cos β3 = s 3
1 2 3

L L L
∴ s = cos1β + cos2β + cos3β
1 2 3
6 11 7
s = cos 49.78° + cos 19.08° + cos 35°
s = 29.48 m

ENGR. EDMIL JHON B. ARIQUES 10

College of Engineering, Architecture and Technology
Name: ____________________________________ Date Submitted: __________
Course & Year: _____________________________ Rating: _________________
Evaluation
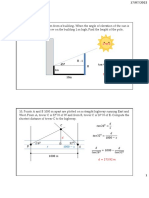
1. The two main cables of the Akashi Kaikyo suspension bridge in Japan have a
span 𝐿 = 1990 𝑚 and a sag 𝐻 = 233 𝑚. The loading on each cable is 𝑤𝑜 =
𝑘𝑁
444.7 𝑚 without traffic) along the horizontal. Determine the corresponding
maximum force in one of the cables.
Answer: 𝑇𝑚𝑎𝑥 = 1.042 𝐺𝑁

ENGR. EDMIL JHON B. ARIQUES 11

 2. Cable AB supports the uniformly distributed load of 4 kN/m. If the slope of the
cable at A is zero, compute (a) the maximum tensile force in the cable; and (b) the
length of the cable.
Answers: a) 𝑇𝑚𝑎𝑥 = 225𝑘𝑁 b) 𝑠(𝐿) = 56.0 𝑚

ENGR. EDMIL JHON B. ARIQUES 12

3. A uniform 80-ft pipe that weighs 960 lb is supported entirely by a cable AB of
negligible weight. Determine the length of the cable and the maximum force in the
cable. (Hint: First locate the point 0 where the cable is tangent to the pipe.)
Answers: 𝑠 = 86.0 𝑓𝑡 𝑇 = 960 𝑙𝑏

ENGR. EDMIL JHON B. ARIQUES 13

 4. The cable carrying 60-lb loads at B and Cis held in the position shown by the
horizontal force 𝑃 = 80 𝑙𝑏 applied at A. Determine h and the forces in segments
BC and CD.
Answers: h = 11.46 ft TBC = 100 lb TCD = 144.2 lb

ENGR. EDMIL JHON B. ARIQUES 14

 5. Find the forces in the three cable segments and the angles 𝛽1 , 𝛽2 and 𝛽3 .
Answers: β1 = 45°, β2 = 10.70°, β3 = 47.22°, TAB = 237.9 lb, TBC = 171.2 lb
TCD = 247.7 lb

ENGR. EDMIL JHON B. ARIQUES 15

 6. The cable carrying three 400-lb loads has a sag at C of ℎ𝑐 = 14 𝑓𝑡. Calculate the
force in each segment of the cable.
Answers: 𝑇𝐴𝐵 = 874 𝑙𝑏, 𝑇𝐵𝐶 = 616 𝑙𝑏, 𝑇𝐶𝐷 = 562 𝑙𝑏 𝑇𝐷𝐸 = 756 𝑙𝑏

ENGR. EDMIL JHON B. ARIQUES 16

Additional Reading:

Engineering Mechanics and Design Applications (Transdisciplinary Engineering

Fundamentals) by Atila Ertas

References:

Hibbeler, R.C. (2016). Engineering Mechanics Statics, Fourteenth Edition. New Jersey:
Pearson Prentice Hall.
Johnston, F.P.,.Beer, E.R., Mazurek, D.F., and Cornwell, P.J. (2013). Vector Mechanics
forEngineers: Statics and Dynamics, Tenth Edition. New York: The McGraw-
Hill Companies, Inc.
Khurmi, R.S. A Textbook of Engineering Mechanics, Twentieth Multicolor Edition. New
Delhi: S. Chand & Company Ltd.
Meriam, J.L. and Kraige, L.G. (2012). Engineering Mechanics Statics, Seventh Edition.
New Jersey: John Wiley & Sons, Inc.
Pytel A. and Kiusalaas J. (2010). Engineering Mechanics Statics, Fourth Edition. Boston:
Cengage Learning
Singer, F.L. (1970). Engineering Mechanics, Second Edition. New York: Harper & Row
Publishers Inc.
Timoshenko S., Young D.H., Rao, J.V. (2007). Engineering Mechanics, Revised Fourth
Edition. New Delhi: Tata McGraw-Hill Publishing Company Ltd.

Prepared by:

ENGR. EDMIL JHON B. ARIQUES

Course Facilitator

Noted:

ENGR. ANACLETO M. CORTEZ JR.

Program Chairman, BSME

Approved:

ENGR. JOHN IKE A. UVAS

Dean, CEAT

ENGR. EDMIL JHON B. ARIQUES 17

ENGR. EDMIL JHON B. ARIQUES 18