Tutorial 3, B.Tech.

Sem IV, Heat and wave equations

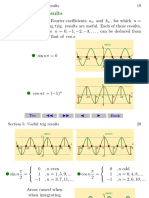
1. A tightly stretched flexible string is fixed at the ends x = 0 and x = L and initially i.e
at t = 0 string is given a shape defined by f (x) = αx(L − x), where α is a constant and
then released from rest. Find the motion of the string at any time t > 0.
2
∞
Ans: 8πL 1
sin (2n−1)πx cos (2n−1)πct
P
π 3 − (2n−1)3 L L
.
n=1

2. A string is fastened ends at x = 0 and x = b executes free vibrations after release from
the initial displacement f (x), and initial speed g(x). Determine the series expansion for

ar
the subsequent displacement y(x, t) when
(i) f (x) = 0.001 sin wx, g(x) = 1 where w is a constant and not integral multiple of π/b.
(ii) f (x) is represented by a triangle with vertices (0, 0), (a, d) and (b, 0).
(iii). f (x) = 0, g(x) = k sin3 (πx/b)
(iv). f (x) = 3a b
x, 0 ≤ x ≤ b/3,

+ 4b
cπ 2
∞
P
n=1
3a
= b (b − 2x), b/3 ≤ x ≤ 2b/3
= 3ab
g(x) = 0.
(x − b), 2b/3 ≤ x ≤ b;

Ans: (i). 0.002π sin bw

1
(2n−1)2
∞
sin b
∞
P
um
n=1
(2n−1)πct
(−1)n+1
n2 π 2 −b2 w2

sin (2n−1)πx
b
sin πx nπct
b cos b
jK
2b2 d 1
sin nπa nπx nπct
P
(ii). a(a−b)π 2 n2 b sin b cos b
n=1
kb πct πx 3πct 3πx
(iii). 12πc [9 sin b sin b − sin b sin b ]
∞
9a 1 2nπ 2nπx 2nπct
P
(iv). π2 n2 sin 3 sin b cos b
n=1

3. A cylindrical homogeneous conducting bar of uniform cross section lies along x–axis with
ends at x = 0, x = L. Lateral surface of bar is insulated. there is no heat source within
the bar. The bar has indicated the initial temperature f (x). Obtain the series expansion
Ra

for the temperature distribution u(x, t) in the bar for t > 0.

(i) Ends are kept at zero temperatures,
f (x) = x, 0 ≤ x ≤ L/2,
= L − x, L/2 ≤ x ≤ L,
(ii) End x = 0 is kept at zero temperature and at x = L there is a constant flux λ,
f (x) = 0.
∞ (2k−1)2 π 2 c2 t
(−1)k+1
Ans: (i). 4L sin (2k−1)πx e−
P
L2
π2 (2k−1)2 L
k=1
∞ (2n−1)2 π 2 t
(−1)n
8a
sin (2n−1)x e−
P
(ii). Ax + π (2n−1)2 2
4

n=1