BOND PRICING

1. C = Coupon = 10%, r = YTM = 12%, N = Maturity = 10 years, Par = $1,000

What is the bond’s price using semi-annual compounding?

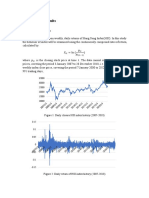
2. a) The graph below depicts the yields on 3-month LIBOR and T-bills. Explain
why is one always on top of the other? What happen to the spread around 2008?

7
6
09/08/2007
5
4 LIBOR
3 T-BILL
15/09/2008
2
1
0
01/02/02

01/08/02

01/08/03

01/08/04

01/02/05

01/08/05

01/02/06

01/02/07

01/02/08

01/08/08

01/08/09
01/08/01

01/02/03

01/02/04

01/08/06

01/08/07

01/02/09

b) Given the information provided in the table below, what is the spread between
the 10-year bond yields between that of Germany and Greece?
Coupon rate Current Price Par Value
Greece 6.00% 24.00 100.00
Germany 2.00% 100.00 100.00

3. a) The yield to maturity on one-year zero-coupon bonds is 9%. The yield to

maturity on two-year zero-coupon bonds is 10%. What is the forward rate of
interest for the second year?
b) What is expectation hypothesis? If you believe in the expectation hypothesis,
what is your best guess as to the expected value of the short-term interest rate
(described in (a)) next year?

c) If you believe in the liquidity preference theory, is your best guess as to next
year’s short-term interest rate higher or lower in (b)? Explain your answer.

d) Discuss the likely reasons underlying an inverted Treasury yield curve in which
the short rates are higher than the long rates.

4. Bond A has a coupon rate of 9% per year paying semi-annually. It has 3 years to
maturity and par value $1,000. Compare the losses incurred by the bondholder if
market interest rates rise by 1% where
i) The current market interest rate is 8%
ii) The current market interest rate is 1%.
Explain the comparative difference in percentage level of loss between the two
circumstances, and discuss the implications of this for bond holders in a low
interest rate marketplace, such as the UK.

Bond Pricing (equivalent formulas)

P=Coupon×( AnnuityF( y , T ) ) + Parvalue×( PvF ( y , T ) )

T
CouponParvalue
P =∑ T
+
t=1 (1+r ) (1+r )T

P=Coupon
([
1
r
1−
1
( 1+r) T ]) +Parvalue
( )
1
(1+r )
T