Fundamentals 9

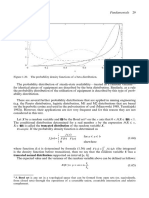
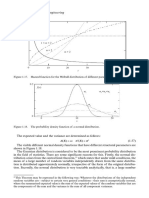
The expected value of a random variable X is a number ascribed to the integral10

(1.17)

where is the domain of determinacy of X.

Several other terms are used to describe this parameter, which include mathematical expec-
tation, mean and mathematical hope. The expected value of a random variable is, in fact, the
weighted average of all possible values that this variable can take on. However, from a rigor-
ous theoretical point of view, the expected value is the integral of the random variable with
respect to its probability measure.
For a discrete random variable that takes the values xi with probabilities pi we have

E( ) ∑x p
i
i i (1.18)

For engineers, it is important to say that the expected value is the centre of gravity of its
probability density.
Some essential properties can be formulated for this mean directly from the definition,
namely:
• The expected value of a constant is simply the value of this constant

E(a) = a (1.19)

• The following relationship holds

E[(aX)k] = ak E(Xk) (1.20)

• The expected value of the linear function of a random variable equals the linear function
of the expected value of this random variable, i.e.

E(aX + b) = aE(X) + b (1.21)

• For a random variable defined as:

Y = X − E(X) we have E(Y) = 0 (1.22)

In the theory of probability and in many of its diverse applications, the expected value is
the most important parameter of a random variable. In engineering practice, the majority of
the so-called nominal parameters of technical objects are just mean values.
The expected value may be intuitively understood by the law of large numbers: the expected
value, when it exists, is almost surely the limit of the sample mean as the sample size increases to
infinity. Nevertheless, the value cannot be expected in the everyday meaning—the expected value
itself may be unlikely or even impossible. The expected value when throwing a dice is 3.5.
By knowing the properties of integrals, we can easily come to the conclusion that not all
random variables have a finite expected value, since the integral may not converge absolutely.

10
This definition differs from the definition usually presented in statistical books. Most commonly, there
is a statement that an expected value is an integral or a sum. However, we obtain a number as the result
of integration (or summation when a random variable is a discrete one) because the integral is a definite
one (Riemann’s integral). By the way, do not try to say to a mining engineer that the average number
of—for instance—shearer knives worn at the mine is an integral.

Book.indb 9 12/9/2013 12:21:57 PM