Rules of Limits

We have seen in the previous section that proving that the limit of a function at some value of x has a specific value is really a tedious task. Moreover, the method we used cannot find us the limit of the function, but only prove the value we know is true. In the following section, we will see how to find the limits of most of the functions we know. Lets see the theorems we use for this object.

Theore m

The limit of the constant function value of x is equal to c. That is,

, where c is a constant, at any

Theore m

The limit of the identity function value of x at that point, or, in symbols:

at some point is equal to the

Theore m

If we have two functions f and g whose limits exist at a number a, then, 1. 2.

3. 4. , in condition that n is any positive integer,

and when n is even. That is a very important theorem to calculate the limits of many functions. It leads us also to the following corollaries.

Corollar y Corollar y Example

If

exists and k is a constant, then:

If

exists and n is any real number, then:

Find:

Solution
Therefore,

The following two corollaries are very helpful. Corollary by: and Let f be the polynomial , where n is function a positive defined integer

are constants. Then the limit of the function f at any number c is:

Corollary NB

Let f be a rational function, and c a number in its domain, then The limit of a function at some point has a unique value. No limit can have two values at the same time. All what we saw before cannot yet be exploited except if the function is defined at the point of the limit. What about the limit when the function has an indeterminate value at some point? The following theorem is the answer.

Theorem

If we have two functions, f and g, such that except possibly at a, and exists, we can say that

, for all

The use of this theorem is indicated by the following example. Example Let f be the function defined by:

Find:

Solution
The function f is a rational function, but 1/3 is not an element of its domain. Hence, we cannot simply substitute in the previous rule of correspondence to get the limit, but using the theorem we have just learnt will make the answer easy. First, note that the function can be rewritten in the form

Now, consider the function , for all . The two functions f and g have the same value at all real numbers except 1/3. Thus, we can say that:

Lim f(x) = lim g(x) = lim (x^2 + 4x 3) = 1/9 + 4/3 3 = 14/9 Thus lim f(x) = g(x)

Theorem

Let f be the function defined by:

such that a is a constant, and n is any real number. Then,

Corollar y Exampl e

If n, m and a are any real constants, then,

Evaluate the limit:

Solution

Theore m

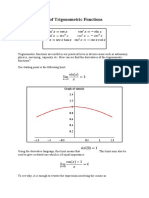
To calculate the limits of some trigonometric functions, the following theorem and corollaries are needed. If x is an angle measured in radians, we say that 1. 2.

Corollar y

If x is an angle measured in radians, and a and b are constants, then 1. 2. Calculate: . .

Exampl e

Limit Definition of the Derivative

Once we know the most basic differentiation formulas and rules, we compute new derivatives using what we already know. We rarely think back to where the basic formulas and rules originated. The geometric meaning of the derivative

f (x)= df(x) / dx
is the slope of the line tangent to y=f(x) at x.

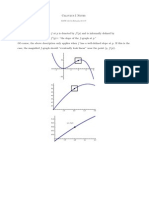
Let's look for this slope at P: The secant line through P and Q has slope
f(x+ x) f(x) =f(x+ x) f(x) (x+ x) x x

We can approximate the tangent line through P by moving Q towards P, decreasing x. In the limit as through Pwith slope
lim x
0 f(x+

0, we get the tangent line

x) f(x) x
0 f(x+

We define

f(x)=lim

x) f(x) x

If the limit as point.

0 at a particular point does not exist, f(x) is undefined at that

We derive all the basic differentiation formulas using this definition.

Example

For f(x)=x2,

f (x) = lim = lim

x 0

((x+ x)^2x^2) /

x x

((x^2+2( x)x+ x^2)x^2) /

x 0

= lim

2( x)x+ x^2 /
x 0(2x+

= lim

x)

= 2x
as expected. Example

For f(x)=x1

f (x) = = = = = lim
again as expected.

x(x+

x1x+ xx1 lim x 0 xx(x+ x)(x+ x)(x) lim x 01(x+ x)(x) 1x2
Notes

x)(x)

lim

The limit definition of the derivative is used to prove many well-known results, including the following:
y y y

If f is differentiable at x0, then f is continuous at x0. Differentiation of polynomials: d / dx x^n =nx^n1 . Product and Quotient Rules for differentiation.

Key Concepts
We define f

(x)=lim

f(x+ x)f(x). x