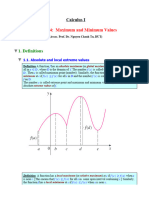
TEXTBOOK NOTES – LOCAL EXTREMA

INCREASING AND DECREASING FUNCTIONS

• Recognize the Behavior: Suppose a function 𝑓𝑓 has a derivative at each point in an open interval. Then

1. 𝑓𝑓 is increasing on the interval if f′(x) >0 for each x in the interval ;

2. 𝑓𝑓 is decreasing on the interval if f′(x) <0 for each x in the interval ;

3. 𝑓𝑓 is constant on the interval if f′(x) =0 for each x in the interval .

CRITICAL NUMBERS

• Increasing/Decreasing Test: To find the intervals on which a function 𝑓𝑓 is increasing or decreasing, do

the following:

Step 1 Compute the derivative f′.

Step 2 Find all numbers for which f′(x) =0 or f′(x) does not exist.

Solve the inequalities f′(x) 70 and f′(x) 60 graphically or algebraically

Step 3 (by testing a number in each of the intervals determined by the numbers found in Step
2).

MAXIMA AND MINIMA

• Local Extrema: Let 𝑐𝑐 be a number in the domain of a function 𝑓𝑓. Then

1. 𝑓𝑓 has a local maximum at 𝑐𝑐 if f (x) <=f (c) for all x near c ;

2. 𝑓𝑓 has a local minimum at 𝑐𝑐 if f (x) >= f (c) for all x near c .

The function 𝑓𝑓 is said to have a local extremum , also known as a

relative extremum , if it has a local maximum or minimum there.

THE FIRST-DERIVATIVE TEST

• First-Derivative Test: Suppose 𝑓𝑓 is differentiable on the interval [𝑎𝑎, 𝑏𝑏] and 𝑐𝑐 is the only critical number
in (𝑎𝑎, 𝑏𝑏).

1. There is a local maximum at 𝑐𝑐 if f′(a) > 0 and f′(b) < 0 .

2. There is a local minimum at 𝑐𝑐 if f′(a) < 0 and f′(b) > 0 .