01

NOTE
P H Y S I C S

MATHEMATICAL TOOLS
INTRODUCTION TO DIFFERENTIATION

What you already know What you will learn

• What is a function • Exponential functions

• Linear and quadratic functions • Logarithmic functions
• Trigonometric functions • Differentiation of a function
• Important trigonometric formulae • Properties of differentiation

SOME IMPORTANT FUNCTIONS

Polynomial Trigonometric Exponential Logarithmic

Functions Functions Functions Functions

NEET
Exponential Functions

• It is a function whose value is a constant

Graph of exponential functions
raised to the power of a variable.
f(x) = b x Exponentially
increasing function 10
• Where b, any number such that b > 0 and
b ≠ 1, is known as the base and x can when b > 1, bx is 8
Exponentially increasing
take the value of any real number. 6
• Example: Radioactivity of certain unstable 4
f(x) = 2x
elements. 2
x
-4 -3 -2 -1 0 1 2 3
Exponentially
10 decreasing function
8 when 0 < b < 1, bx is
Exponentially decreasing
6
4
2 g(x) = 0.5x
x
-3 -2 -1 0 1 2 3 4

© 2020, BYJU'S. All rights reserved

 02

Natural Exponential Function

y
An exponential function whose base is the
Euler’s number ‘e’, is known as a natural
exponential function.
y = f(x) = ex

Euler’s number (𝑒) ≈ 2.718

(0,1)
x

Value of exponential function can not be negative.

As b > 0 for any value of x, b x > 0

Given the function f(x) = 4x, evaluate the following:

(i) f (−3) (ii) 𝑓 − 1

4

Solution

1 1  −1 
−1
1 1 1
(a) f ( −3) = 4 =
−3
= (b) f  =  4=
4
= =
43 64  4 
1 1
2
44 22

NEET
Logarithmic Function

• They are the inverse of exponential functions. They are represented as: f(x) = loga (x).
• Where x > 0 and a, also known as base, takes any value greater than 0, except 1. This
function implies that, y = loga x ⇒ x = ay.

Think what will happen if you put a = 1.

𝑥 = 1𝑦
Which means x can only be 1 for any value of y.
So, log1 1 could be any number.

Natural Logarithm

If base = e, f (x) = loge (x) = ln (x)

© 2020, BYJU'S. All rights reserved

 03

Common Logarithm

If base = 10, f (x) = log10 (x)

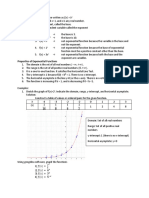
Graph of a logarithmic function

• Graph is always on the positive side of x-axis.

• It always intersects the x-axis at x = 1, i.e., it passes through (1,0).
• At x = b, f(x) = logb (b) = 1. Hence, the graph always passes through (b, 1).

𝒚 f(x) = logbx; b > 1 𝒚 f(x) = logbx; 0 < b < 1

(𝒃, 𝟏)
(𝒃, 𝟏)
𝒙 𝒙
(𝟏,𝟎)
(𝟏,𝟎)

Properties of Logarithmic Functions

1 Product Rule log𝑏 𝑚𝑛 = log𝑏 𝑚 + log𝑏 𝑛

2 Quotient Rule log𝑏 m = log𝑏 𝑚− log𝑏 n

n

3 Power Rule log𝑏 𝑚p = p. log𝑏 𝑚

If log10 2 = 0.3010 and log10 3 = 0.4771, then find the approximate value of log10 36.

Solution

log10 36 = log10 62 = 2 log10 6

= 2 log10 (3 × 2) = 2(log10 3 + log10 2)
= 2(0.3010 + 0.4771) ≅ 1.56

© 2020, BYJU'S. All rights reserved

 04

BOARDS
Tangent - The limiting case of secant

y y y y
Secant
B B
B
Tangent
A Δy A Δy A Δy A, B (P)
Δx Δx Δx
x x x x
∆𝒚 ∆𝒚 ∆𝒚
Slope = Slope = Slope = Slope = ?
∆𝒙 ∆𝒙 ∆𝒙

Tangent
• A line that touches the curve at one point.
• A limiting case of secant that intersects the curve at two
Slope of Slope of
infinitesimally close points.
Secant Tangent
• The derivative of a function at a point gives the slope of tangent
∆ y dy
at that point. ∆𝒚 lim =
∆ x →0 ∆ x dx
• For any function y = f (x), slope of tangent at a point indicates ∆𝒙
the rate of change of y with respect to x at that point.

Differentiation

Differentiation

• It is the study of variation of one quantity with respect to to differentiate

another quantity. We can find the rate of change of a function
using differentiation. to find the derivative
𝒅𝒚
• It is denoted by the notation: , where y = f(x) is a function.
𝒅𝒙 𝒅𝒚
𝒚′=𝒇′ (𝒙)=
𝒅𝒙

Derivatives of Functions

d d d
(sin x) = cos x (cosec x) = - cosec x cot x (cot x) = - cosec2 x
dx dx dx

d d n d
(cos x) = - sin x (x ) = nxn−1 Power Rule (sec x) = sec x tan x
dx dx dx

d d 1 d x
(tan x) = sec2 x (ln x) = (e ) = ex
dx dx x dx

© 2020, BYJU'S. All rights reserved

 05

d ( 4)
Derivative of any constant function is zero. For example = 0.
dx

Differentiate the following,

1
(a) f ( x ) = x3 , with respect to 𝑥 (b) f ( x ) = , with respect to 𝑥
x
3
(c) f ( x ) = x 4 , with respect to 𝑥 (d) f ( x ) = x , with respect to 𝑥

Solution

1
3 d  d ( x −1 )
dx  x −1
(a) = 3=
x 3−1
3 x (b)
2
= −1 x −1−1 =
=
dx dx dx x2

 3  1
d  x4 
(c) =   x
=
3 
3  4 − 1
= x
 −1 
3  4  3
(d)
d (=
x)
d  x2 
=  1 12 − 1
x
=
1 −21
= x
1
dx 4 4 1
dx dx 2 2 2 x
4x 4

BOARDS
Properties of Derivatives

• (Derivative of a Constant) × (Function) = (Constant) × (Derivative of the Function)

𝒅 𝒅𝒇(𝒙)
(𝒂𝒇(𝒙)) = 𝒂
𝒅𝒙 𝒅𝒙
• Derivative of sum or difference of two functions = Sum or difference of the derivative of the
functions
𝒅 𝒅𝒇(𝒙) 𝒅𝒈(𝒙)
(𝒇(𝒙) ± 𝒈(𝒙)) = ±
𝒅𝒙 𝒅𝒙 𝒅𝒙

Differentiate f (x) = 2 cos (x) - 6 sec (x) + 3

Solution
𝑑𝑓 𝑑 𝑑 d
𝑓′ (𝑥) = =2 (cos 𝑥) − 6 (sec 𝑥) + (3)
𝑑𝑥 𝑑𝑥 𝑑𝑥 dx
f′ (x) = −2 sin x − 6 sec x tan x

© 2020, BYJU'S. All rights reserved

 06

Product Rule

d(f(x).g(x)) df(x) dg(x)

= g(x) + f(x)
dx dx dx
d d d
Example: (x sin x) = sin x. (x) + x. (sin x)
dx dx dx
= sin x + x cos x

Differentiate y = f (w) = tan (w) sec (w) with respect to w.

Solution

𝑑𝑓 𝑑
= (tan(𝑤).sec(𝑤))
𝑑𝑤 𝑑𝑤
𝑑 𝑑
= tan (𝑤) sec (𝑤) + sec (𝑤) tan (𝑤)
𝑑𝑤 𝑑𝑤
= tan(𝑤) {sec(𝑤) tan(𝑤)} + sec(𝑤) {sec2 (𝑤)}
= sec(𝑤) tan2(𝑤) + sec3(𝑤)
dy
y′= = f ′ (w) = sec(w) tan2(w) + sec3(w)
dw

Division Rule

𝒅𝒇(𝒙) 𝒅𝒈(𝒙)
𝒈(𝒙) − 𝒇(𝒙)
𝒅 𝒇(𝒙) 𝒅𝒙 𝒅𝒙
=
𝒅𝒙 𝒈(𝒙) (𝒈(𝒙))𝟐
d d
cos x. (sin x) − sin x. cos x
d d sin x dx dx
Example: (tan x) = =
dx dx cos x cos2 x
sin2 x + cos2 x
= = tan2 x + 1 = sec2 x
cos2 x

Chain Rule

If f = f (g) and g = g (x), then,

df
=
df dg
. Example:
(
d sin ( x 2 )
=
) cos ( x 2 ) ×
dx 2
= cos ( x 2 ) × 2 x
dx dg dx dx dx

© 2020, BYJU'S. All rights reserved

 07

1
Differentiate g (t) = with respect to t.
(4t − 3t + 2)2
2

Solution

𝑑𝑔 𝑑
𝑔′ (𝑡) = = −2(4𝑡2 − 3𝑡 + 2)−2−1 (4𝑡2 − 3𝑡 + 2)
𝑑𝑡 𝑑𝑡
= −2(4𝑡2 − 3𝑡 + 2)−3 (4(2𝑡) − 3)
2(8t − 3)
= −
(4t2 − 3t + 2)3
dg –2(8t − 3)
𝑔′ (t) = =
dt (4t2 − 3t + 2)3

Double Differentiation

𝑑2𝑦 𝑑 𝑑𝑦
f (x) =
𝑑𝑥2 𝑑𝑥 𝑑𝑥

f (x) = sin (x)

f ’ (x) = cos (x)
f ’’ (x) = -sin (x)
𝑑 𝑑 f’’(x)
𝑑𝑥 𝑑𝑥

f’(x)
d2 y
Example: If y = cos(x2), what is ?
dx2
Differentiate the first time using the chain rule.
dy d
⇒ = – sin x2 × (𝑥2) = − sin x2 × 2x = – 2x sin x2
𝑑𝑥 𝑑𝑥

Differentiate the second time using the product rule and the chain rule.
𝑑2 𝑦 d d
= sin x2 × (-2x) + (-2x) × (sin x2)
𝑑𝑥 2
𝑑𝑥 𝑑𝑥
= −2 sin x2 − 2x cos x2 × (2x)
d𝟐 y
y′′= = −2 sin (x2) −4x2 cos (x2)
dx𝟐

© 2020, BYJU'S. All rights reserved