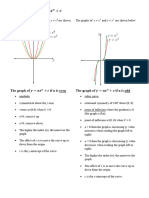
The cubic curve 𝒚𝒚 = 𝒂𝒂𝒙𝒙𝟑𝟑 + 𝒄𝒄

An equation in which the highest power of the variable is 3 is called a cubic equation.
The graph is called a cubic curve.
The graph of 𝒚𝒚 = 𝒂𝒂𝒙𝒙𝟑𝟑

• The graph has no axis of symmetry.

• The graph has rotational symmetry of 180o about (0,0): If you spin the curve upside-down, it maps
onto itself.
• If a > 0, the graph is always increasing except at (0,0)
• If a < 0, the graph is always decreasing except at (0,0)
• The size of a determines whether the cubic curve is ‘wider’ or ‘narrower’.
The graph of 𝒚𝒚 = 𝒂𝒂𝒙𝒙𝟑𝟑 + 𝒄𝒄

The effect of c (the y-intercept) is to move the cubic curve up or down from the origin.

Example:

1) Graph the cubic equations y =x3 + 1, y =− x3 + 3 and y =−3 x 3 − 5 , showing the y-intercept of each
curve.