Path Loss

Multipath Fading

Multipath fading

Instructor: M.A. Ingram

ECE4823
Interference
Shadowing

Excess Delay

Strength Variation

The propagation delay relative to that of the

shortest path

As the vehicle moves over a short distance, the

strength of each path varies because the surfaces are
complex

=8s

=0

=47s

The Channel is a Filter

Measured Data from

Darmstadt, Germany

[Molisch, 01]

The multipath channel can be

represented as linear, time-varying
bandpass filter
Transmitted
Signal

h(t , )

x(t)

Received
Signal

y(t)

y (t ) =

x(t )h(t , )d

Baseband Impulse Response

Path Model

More convenient to work with baseband

signals

{
}
x(t ) = Re{ c(t )e }
y (t ) = Re{ r (t )e }

h(t , ) = Re hb (t , )e j ct
j c t

hb (t , )

j c t

The channel may be probed or sounded by

transmitting a pulse p(t) and recording the
response at the receiver
The response is the convolution of p(t) with
the channel impulse response

r (t ) =

1 N 1
i (t )e ji (t ) p(t i )
2 i =0

r (t ) =
r(t)

hb ( t , )

0 1 2 3 4

(t )e
i =0

4 (t )

delay

p(t)

Tp

delay

Time Variation of the Probe

Response

The magnitude squared of any sample in the interval 4 and

0 + Tp will equal
2
N 1

hb ( t , )

Instantaneous Power
2

3 (t )e j ( t) 4 (t )e j

Suppose a pulse much wider than the length

of the impulse response is transmitted at time
t=0

0 1 2 3 4

2 (t )

Pulse Width >> max

Probing the Channel

N =5

0 ( t ) e j ( t )
1 (t )e j ( t ) (t )e j
2

The factor of
ensures that baseband
average power
equals passband
average power

1
r (t ) = c(t )hb (t , )d
2

The channel is assumed to comprise N

discrete paths of propagation (rays)
Each path has an amplitude (t), a phase (t)
and a propagation delay

j i ( t )

If one or both of the terminals moves, the path

phases change because the path lengths change
The path amplitudes do not change much
These changes yield large changes in the magnitude
of the received waveform

|r(t)| in dBm

[not real data]

We say, the multipath is not resolved

delay

Average Power for

Narrowband Signals

Narrowband Fading

This same type of fading happens to a

digital waveform if the symbol period is
much larger than (>10 times) the
channel length
Such long symbol periods correspond to
narrowband signals

}
N

i =0

where

1

T
2
i

t+

T
2

2
i

T
2

2
4

( s )e
i =0

2
j i ( s )

ds

p(t)

Tp

( s )ds
0

delay

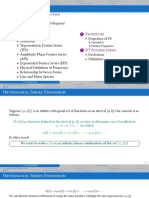
The Fourier Transform of such a narrow

pulse has a wide spectrum
P(f)

p(t)
t)
j
3 (t )e j (
4 (t )e
3

Wideband Signal

T
2

hb (t , )

r (t , )
2 (t )

t+

Pulses do not overlap

Now consider a small pulse width

T
t
2

0 (t )e j ( t )
t)
j
1 (t )e j (
2 (t )e

where the interval [t-T/2,t+T/2] corresponds

to a local area

2
i

Multipath Resolved

E r (t )

Assume that the phases of different paths are

uncorrelated
Then the time average simplifies to

E r (t )

Assuming the channel is ergodic, the

ensemble average may be approximated by a
time average:

Pulse Width << max

Uncorrelated Scattering

4 (t )

Tp

F.T.

Average Power for Wideband

Signals

Power Delay Profile (PDP)

The PDP is a time-average of |r(t,)|2 over a

small interval (assuming the terminal is
T
moving)
t+

P ( )
P( )

2 02

212

2 22

1
T

N 1

= i2
i =0

2
4

Narrowband and Wideband averaged

powers are equal

Moments of the PDP

Mean Delay

Must first compute the mean delay

+

P( )d
0

T
2

2 32

The average power is the integral of the

PDP
PAVG =

r (s, ) ds

Local Average Powers Are The

Same

P( )d
0
+

P( )d
0

For this to be mean excess delay, the origin

of the axis needs to be the time of the first
arriving path

Channels are often described by their

rms delay spread
To compute rms delay spread,
normalize the PDP to make it like a PDF
for a random variable (unit area) and
then find its standard deviation
Must you use excess delay to compute
rms delay spread?

Second Moment

Next need the second moment of this

PDF
+
2
0 P( )d
2
= +
P( )d
0

RMS Delay Spread

Example Data

Recall that standard deviation is the

square root of variance and variance is
the second moment minus the first
moment squared
Variance

rms delay spread

()
( )

2 = 2

= 2

How RMS Delay Spread Can

Be Used

The Frequency Domain View

If <<symbol period, assume

narrowband fading effects
If >>symbol period, assume
wideband fading effects (will need an
equalizer, CDMA or OFDM)

Narrowband Case

[Rappaport, 02]

Transmitted
Signal Spectrum

900z

<<symbol period implies that the

frequency response of the channel,
+

H (t , f ) = h(t , ) exp( j 2f )d ,

doesnt vary much with frequency over

the bandwidth of the transmitted signal

Flat Fading

The channel appears flat to the signal

H (t , f )

When <<symbol period, we say the

signal undergoes flat fading
The channel frequency response is
approximately flat over the signal
bandwidth

Wideband Case

Frequency Selective Fading

>> symbol period implies that the

frequency response of the channel varies
significantly with frequency over the
bandwidth of the transmitted signal

H (t , f )

Summary

The multipath channel model has a discrete number

of propagation paths
Each path has amplitude, phase and delay
The PDP is the local average of the magnitude
squared of the impulse response of the channel
Average power of the channel is the integral of the
PDP
Average power is same for narrowband and
wideband channels
The fading is flat or frequency selective
depending on the comparison between rms delay
spread and the symbol period

When >> symbol period, we say the

signal undergoes frequency selective

fading

Transmitted
Signal Spectrum

900z

The channel frequency response is

strong for some frequencies and not for
others within the signal bandwidth

References

[Rapp, 02] T.S. Rappaport, Wireless

Communications, Prentice Hall, 2002
[Molisch, 01] Andreas F. Molisch (ed),

Wideband Wireless Digital

Communications, Prentice Hall PTR,
2001.