ADDITIONAL MATHEMATICS

DIFFERENTIATION OF FUNCTIONS
Differentiation
Formulas
When and How to Use
Power Function
( )
1 n n
d
ax anx
dx

=

1)
( )
3 2
5 15
d
x x
dx
= 2)
5 4
2 10
3 3
d
x x
dx
| |
=
|
\ .
3)
( )
3 4
4 12
d
x x
dx

=
Linear Function
( )
d
ax a
dx
=

1)
5 5
12 12
d
x
dx
| |
=
|
\ .
2)
( ) 3.75 3.75
d
x
dx
=
Constant
( ) 0
d
a
dx
=

1)
4
0
3
d
dx
| |
=
|
\ .

Chain Rule
dy dy du
dx du dx
=
Normal Method
( )
( )
10
2
2
10 9
9
9 2
2 5
2 5, 4
, 10
sin ,
10 4 10 2 5 4
y x
du
Let u x therefore x
dx
dy
Now y u u
du
dy dy du
ce
dx du dx
dy
therefore u x x x
dx
=
= =
= =
=
= =

Short-Cut Method
( )
10
2
2 9
2 5
10(2 5) 4
y x
x x
=


Sum of Functions
( )
d du dv
u v
dx dx dx
+ = +

3 2
2 2
4 12
3 3
d
x x x
dx
| |
+ = +
|
\ .

Difference of
Functions
( )
d du dv
u v
dx dx dx
=

( )
2 3 1 2
7 13 14 39
d
x x x x
dx
=
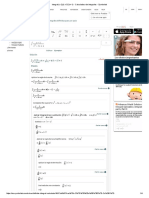
Product Rule
( )
d dv du
uv u v
dx dx dx
= +

3 2
3 2
2
2 2 3
(2 6 )(5 3 )
2 6 , 6 6
5 3 , 6
(5 3 )(6 6) (2 6 )( 6 )
y x x x
du
Let u x x therefore x
dx
dv
Let v x therefore x
dx
dy du dv
Since v u
dx dx dx
dy
Therefore x x x x x
dx
Expand and Simplify
= +
= + = +
= =
= +
= + + +

Differentiate Outside First
Then Differentiate Inside
ADDITIONAL MATHEMATICS
DIFFERENTIATION OF FUNCTIONS

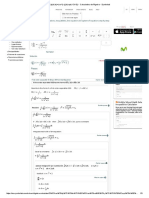
Quotient Rule
2
( )
du dv
v u
d u
dx dx
dx v v

=
Normal Method
2
3
2
3 2
2
3 2 2
3 2
2 1
3 5
2 1, 4
3 5 , 3 15
( )
(3 5 )(4 ) (2 1)(3 15 )
(3 5 )
x
y
x x
du
Let u x therefore x
dx
dv
Let v x x therefore x
dx
du dv
v u
d u
dx dx
Since
dx v v
x x x x x
Therefore
x x
Expand and Simplify

= =
= =

Short-Cut Method
2
3
2 3 1
2 1
3 5
(2 1)(3 5 )
x
y
x x
Change to the form y x x x
Use PRODUCT RULE to Differentiate
Expand and Simplify

=
The End