Appendix A Review

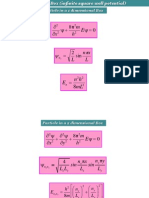
Barrier Penetration
For a one-dimensional potential, free particles of mass m and energy E are
represented by plane waves that are incident from the left and encounter the
rectangle potential of height V, where V > E. In the region x < 0, the incoming wave
eikx travels from left to right. At the barrier, a wave is reflected back and travels from
right to left with equation e-ikx. The total wavefunction at x < 0 is then 1(x) =
Aeikx+Be-ikx, with A and B being complex constants, and wave number k given by
2k2 = 2mE.
In the region 0 < x < a, the solution to the Schrodinger equation is a decaying
exponential added with an exponential wave reflected from the boundary at x=a.
This wavefunction is 2(x) = Ce-kx+Dekx, with C and D being complex constants and
given by 2 2 = 2m(V-E).
In region x > a, there only exists a wave moving from left to right with equation
3(x) = Feikx, where F is a complex constant.
The transmission coefficient, T, is defined by T = |F/A| 2. F and A are found by using
the continuity of the wave function and the first derivatives. They have to match at
the boundaries of x = 0 and x = a.
Density of States
A spinless particle, mass m, inside a cube of sides L and volume V = L3. The cube
has point (0, 0, 0) at the origin and edges parallel to x, y, and z axes. Potential is
zero in the box thus the walls are considered of infinite potential barriers and the
solutions to the Schrodinger equation vanish at the boundaries. The solutions are
standing waves of the form (x,y,z) = C sin(k xx)sin(kyy)sin(kzz). C is a constant and
the wave number K = (kx,ky,kz), where ki = ni/L, where i=x,y,z, and ni = 1,2,3,.
Particle energy is given by E = (1/2m)(/L)2(nx2 + ny2 + nz2).
Allowed values of k form a cubic lattice in a quadrant of k-space where all values of
ni are positive. Since each state corresponds to one combination of (n x, ny, nz), the
number of allowed states is equal to the number of lattice points. The spacing
between the states is (/L) so the density of points per unit volume in k-space is
(L/)3. The number of lattice points n(k0) with k less than k0, is the number contained
within a volume that for large values of k0 may be approximated by a quadrant of a
sphere of radius k0: n(k0) = (V/83)(4/3)(k03).
The density of states is