Scribd Logo
Upload

Welcome to Scribd!

  • Lalapalooza PDF

    Uploaded by

    ThisIsSoRandom
    6 views1 page
    This document discusses evaluating limits of functions using an intuitive approach. It provides an example of evaluating the limit as x approaches 2 of the function x^2/(x^2 - 5x + 4 + 6). The solution works through transforming the indeterminate form of 00 into a determinate limit by factorizing the top and bottom into (x - 2)(x - 3) giving the limit of 1 as x approaches 2.

    Original Description:

    Original Title

    lalapalooza.pdf

    Copyright

    © © All Rights Reserved

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    Report this Document
    This document discusses evaluating limits of functions using an intuitive approach. It provides an example of evaluating the limit as x approaches 2 of the function x^2/(x^2 - 5x + 4 + 6). The solution works through transforming the indeterminate form of 00 into a determinate limit by factorizing the top and bottom into (x - 2)(x - 3) giving the limit of 1 as x approaches 2.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content
    6 views1 page

    Lalapalooza PDF

    Uploaded by

    ThisIsSoRandom
    This document discusses evaluating limits of functions using an intuitive approach. It provides an example of evaluating the limit as x approaches 2 of the function x^2/(x^2 - 5x + 4 + 6). The solution works through transforming the indeterminate form of 00 into a determinate limit by factorizing the top and bottom into (x - 2)(x - 3) giving the limit of 1 as x approaches 2.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content
    of 1

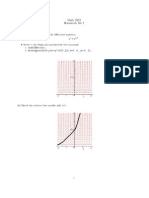
    = x + 1, when x = 1.

    1.1. LIMIT OF A FUNCTION: AN INTUITIVE APPROACH 7


    Therefore, we obtain the limit as follows:
    x! lim 1
    x2 + x + 2x 1 + 1
    = x! lim 1(x +1)=0
    Example 1.1.19. Evaluate x!2
    lim x2 x2 5x 4 + 6
    .
    Solution.
    Note that x!2
    lim x2 x2 5x 4 + 6
    is an indeterminate form of type 00 . Using the same technique,

    x!2 lim x2 x2 5x 4+6


    = x!2

    lim (x (x 2)(x 2)(x + 3

    You might also like