"What the mind of man can conceive

14
and believe, it can achieve."
…..Napoleon Hill
CHAPTER

Calculus
Learning Objectives
After reading this chapter, you will know:
1. Indeterminate form
2. Derivative
3. Maxima-Minima
4. Integration
5. Vector Calculus

Indeterminate Form
0 ∞
1. ,
0 ∞
2. 0 × ∞, ∞ − ∞, ∞ × ∞
3. ∞0 , 00 , 1∞
Example: Plot y= [x]
Here [x] ⇒ Greatest integer not greater than x
−2 ≤ x < −1, y = −2
−1 ≤ x < 0, y=−1
0 ≤ x < 1, y=0
1 ≤ x < 2, y=2

Various Plots

y y y y
Y =ax Y =ax
Y =ex Y =In
0 < a <1 0 < a <1
x x x x

Limit of a Function
Let y = f(x)
Then limx→a f(x) = l i.e., “f(x)→ l as x→a” implies for any x ∈(>0), δ(>0) such that whenever
0<|x − a|<δ , |f(x) − l |<∈

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 42

 Calculus

Some Standard Expansions

n(n−1) 2 n(n − 1)(n − 2) 3
(1 + x)n = 1 + nx + x + x +. . . . . . . . . x n
2! 3!
x n − an
= x n−1 + x n−2 a + x n−3 a2 +. . . . . . . . . an−1
x−a
x
x2 x3
e = 1 + x + + .........
2! 3!
x2 x3
log (1 + x) = x − + .........
2 3
x2 x3
log (1 − x) = − x − − . . . . . . . . .
2 3
x3 x5 x7
sin x = x − + − .........
3! 5! 7!
x2 x4 x6
cos x = 1 − + − .........
2! 4! 6!
x3 x5 x7
sin h x = x + + + . . . . . . . . .
3! 5! 7!
x2 x4 x6
cos h x = 1 + + + .........
2! 4! 6!

Some Important Limits

sinx
lim =1
x→0 x
1 x
lim (1 + ) = e
x→∞ x
1
lim(1 + x)x = e
x→0
ax − 1
lim = log e a
x→0 x
ex − 1
lim =1
x→0 x
log(1 + x)
lim =1
x→0 x
x n − an
lim = n an−1
x→a x − a

L – Hospital’s Rule
0 ∞
 When functions are of 0
or ∞
form differentiate Numerator & Denominator and then apply
limit.

Existence of Limits and Continuity

 f(x) is defined at a, i.e., f(a) exists.
 If lim f(x) = lim f(x) = L
x→a+ x→a−
Then, the lim f(x) exists and equal to L.
x→a
 If limx→a+ f(x) = limx→a− f(x) = f(a) then the function f(x) is said to be continuous.

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 43

 Calculus

Properties of Continuity
 If f and g are two continuous functions at a; then
 (f + g), (f × g), (f − g) are continuous at a
f
 is continuous at a, provided g(a) ≠ 0
g
 |f| or |g| is continuous at a

x3 −a3
Example: limx→a
x2 −a2
Solution: Using the formula above,
x 3 − a3
lim 2
x→a x − a2
x 3 − a3
= lim 2
x→a x − a2
x 3 − a3 1 1 3a
= lim × lim = 3 a3−1 =
x→a x − a x→a x + a 2a 2
1
Example: limx→0(1 − x 2 )x
1 1 1
Solution: limx→0 (1 − x 2 )x = limx→0(1 − x)x × limx→0(1 + x)x = e e−1 = 1

12 22 n2
Example: Evaluate lim [ n3 + n3
+ − − − − − − − − − − − − − − + n3
]
n→∞
1 + 2 + − − − − − − − − − − − − − + n2
2 2
Solution: limn→∞ [ n3
]
n(n + 1)(2n + 1)
= lim [ ]
n→∞ 6n3
(n + 1)(2n + 1) 1×2 1
= lim [ ] = =
n→∞ 6n2 6 3

x3
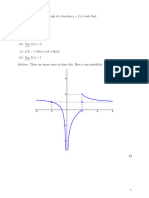
Example: Find the limit lim | | if possible
x→0 x
−x 3
𝐒𝐨𝐥𝐮𝐭𝐢𝐨𝐧: x < 0, lim = −x 2 = 0
x→0 x
x3
x > 0, lim = x2 = 0
x→0 x
Hence lim f(x) = 0
x→0

1
ex
𝐄𝐱𝐚𝐦𝐩𝐥𝐞: f(x) = 1 when x ≠ 0
1+ ex
= 0 when x = 0
1
ex 1 e−∞ 0
Solution: lim f(x) = lim 1 = lim 1 = 1+e−∞ = 1+0
= 0
x→0− x→0− 1+ex x→0− −
1+e x
1
ex 1 1
lim f(x) = lim 1 = lim 1 = = 1
x→0+ x→0+ x→0+ 1 + e∞
1+ ex 1 + e− x
Here limits does not exists also discontinuous at x =0

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 44

 Calculus

Rolle’s Theorem
If
(i) f(x) is continuous in closed interval [a,b].
(ii) f ′ (x) exists for every value of x in open interval (a,b).
(ii) f(a) = f(b) then there exists at least one point c between (a, b) such that f ′ (c) = 0.

Geometrically, there exists at least one point c between (a, b) such that tangent at c is parallel to x
axis.

f(b
f(a)
)

a c b
Rolle’s Mean Value Theorem

If (i) f(x) is continuous in the closed interval [a,b] and

(ii) f ′ (x) exists in the open interval (a,b), then atleast one value c of x exist in (a,b) such that
f(b) − f(a)
= f ′ (c)
b−a

Geometrically, it means that at point c, tangent is parallel to the chord line.

f(b)

f(a)

a c b
Lagrange Mean Value Theorem

Let f1 and f2 be two functions such that:

(i) f1 , f2 both are continuous in [a, b]
(ii) f1 , f2 both are differentiable in (a, b)
(iii) f2′ (x) ≠ 0 in (a, b) then,
For a < β < b
f1 (b) − f1 (a) f1′ (β)
=
f2 (b) − f2 (a) f2′ (β)

π π
Example: f(x) = cosx, a = − 2 , b = 2 ; find c from Rolle’s theorem
Solution: f(x) = cos x
f ′ (x) = −sin x

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 45

 Calculus

π π
f (− ) = cos (− ) = 0
2 2
π π
f ( ) = cos = 0
2 2
Hence f ′ (c) = 0 ⇒ − sin x = 0
x=0

Example: Find c using Lagrange’s Mean value theorem from f(x) = 3x 2 + 5x + 7 in interval [1 ,3]
Solution: f(1) = 15
f(3) = 49
f ′ (x) = 6x +5
a = 1, b =3
f(b) − f(a)
f ′ (c) =
b−a
49 − 15
6c + 5 =
3−1
34
6c + 5 = = 17
2
12
c = = 2
6

Example: f(x) = ln x in interval [1, e]

1
f ′ (x) =
x
f(b) − f(a)
f ′ (c) =
b−a
1 log ee − log1e
=
c e−1
1−0
=
e−1
c= e−1

Derivative
f(x + h) − f(h)
f ′ (x) = lim
h→0 h
Provided the limit exists f ′ (x) is called the rate of change of f at x
Algebra of derivative:-
(i) (f + g)′ = f ′ + g ′
(ii) (f − g)′ = f ′ – g ′
(iii) (f g)′ = f ′ g + f g ′
g f ′ − f g′
(iv) (f⁄g)′ =
g2

Derivative of a Function of Function: Chain Rule

dy dy du
=
dx du dx

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 46

 Calculus

y
Homogenous Function: Any function f(x, y) which can be expressed in from x n ϕ (x) is called
homogenous function of order n in x and y. (Every term is of nth degree)
f(n, y) = a0 xn + a1 x n−1 y + a2 x n−2 y 2 +. . . . +an yn
y
f(x, y) = x n ϕ ( )
x

Euler’s Theorem on Homogenous Function: If u be a homogenous function of order n in x and y then,

∂u ∂u
 x +y = nu
∂x ∂y
∂2 u ∂2 u ∂2 u
 x2 + 2xy + y2 = n(n − 1)u
∂x 2 ∂x ∂y ∂y2

Total Derivative
If u=f(x,y), x = ϕ(t) and y=Ψ(t)
du ∂u dx ∂u dy
= +
dt ∂x dt ∂y dt
∂u ∂u
∆u = ∆x + ∆y
∂x ∂y

∂z ∂z
𝐄𝐱𝐚𝐦𝐩𝐥𝐞: If z = log(x 2 + xy + y 2 ), show that x + y =2
∂x ∂y
ez = x 2 + xy + y 2 → Homogenous
∂f ∂f
x +y = 2f
∂x ∂y
∂z ∂z
x ez + y ez = 2ez
∂x ∂y
∂z ∂z
x + y =2
∂x ∂y

Monotonicity of a Function f(x)

1. f(x) is increasing function if α > β , f(α) > f(β)
Necessary and sufficient condition, f ′ (x) > 0
2. f(x) is decreasing function if for α > β, f(α) < f(β)
Necessary and sufficient condition, f ′ (x) < 0

Maxima-Minima
Two Types a) Global b) Local

Rule for Finding Maxima & Minima

 If maximum or minimum value of f(x) is to be found, let y = f(x)
 Find dy/dx and equate it to zero and from this find the values of x, say x is α, β, …(called the
stationary points where x = α1 β1… have maxima or minima are critical points)
d2 y
 Find dx2 at x = α

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 47

 Calculus

d2 y
If > 0, y has a minimum value
dx 2
d2 y
If 2 < 0, y has a maximum value
dx
d2 y
If 2 = 0, proceed further and find at x = α
dx
d3 y
If 3 ≠ 0, y has neither maximum nor minimum value at x = α
dx
d3 y d4 y
But If 3 = 0, proceed further and find 4 at x = α
dx dx
d4 y
If 4 > 0, y has minimum value
dx
d4 y
If 4 < 0, y has maximum value
dx
d4 y
If 4 = 0, proceed further
dx
Note:
Extreme (maxima or minima) value exists either at critical point or at the end point of interval.

Point of Inflexion
If at a point, the following conditions are met, then such point is called point of inflexion

Point of
Inflexion
(i) F”(x) = 0
(ii) F” (x + 8) and F”(x – 8) for 𝛿 > 0 be of opposite sign

Taylor Series
h2 ′′
f(a + h) = f(a) + h f ′ (a) + f (a) + . . . . . . . . .
2!
(x − a)2
for x = a + h then f(x) = f(a) + (x – a) f’(a) + f"(a) + ⋯
2!

Maclaurian’s Series
x 2 ′′ x3
f(x) = f(0) + x f ′ (0) + f (0)+ f ′′′ (a)
2! 3!

Taylor Series for Factors of Two Variables

f(x, y) = f(a, b) + [(x − a)fx (a, b) + (y − b)fy (a, b)]
1
+ [(x − a)2 fxx (a, b) + 2(x − a)(y − b) fxy (a, b) + (y − b)2 fyy (a, b)]+……
2!

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 48

 Calculus

Maxima & Minima (Two Variables)

∂2 f ∂2 f ∂2 f
r = , s = , t =
∂x 2 ∂x ∂y ∂y 2
∂f ∂f
1) = 0, = 0 → Solve these equations
∂x ∂y
2) (i) If rt − s 2 > 0 and r < 0 ⟹Maximum at (a, b)
(ii) If rt− s 2> 0 and r > 0 ⟹Minimum at (a, b)
(iii) If rt − s 2 < 0 at (a, b), f(a,b) is not an extreme value i.e., f(a, b) is saddle point
(iv) If rt −s 2 = 0 at (a, b)
(v) It is doubtful, need further investigation

Example: Find maximum and minimum value of f(x) = 2x 3 − 15x 2 + 36x + 1

Solution: f ′ (x) = 6x 2 − 30x + 36 = 0
x 2 − 5x + 6 = 0
x = 2, 3
f"(x) = 12x − 30
f"(x) |x= 2= − 6 < 0 ⟹ Maximum
f"(x) |x= 3= + 6 > 0 ⟹ Minimum
Maximum value @ x = 2 = 16− 60 +72 +11 = 39
Minimum value @ x =3 = 54 − 135 +108 +11 =173 − 135 = 38

1
Example: Show that maximum value of f(x) = x + x is less than its minimum value.
1
Solution: y = x + x
dy 1
= 1 − 2 = 0, x 2 = 1
dx x
x=±1
d2 y 2
2
= 0 + 3
dx x
d2 y
At x = 1, 2 = 2 ⟹ minimum
dx
d2 y
At x = −1, 2 = −2 ⟹ maximum
dx
1
Maximum value @ x = −1 =−1 + −1 = −2
1
Minimum value @ x = +1 = 1 +1 = 2

Example: Find the maxima and minima of

f(x) = x 5 − 5x 4 + 5x 3 − 1
Solution: f′(x) = 5x 4 − 20x 3 + 15x 2 = 0
5x 2 (x 2 − 4x + 3) = 0
x =0, 1, 3
f"(x) = 20x 3 − 60x 2 + 30x
f"(x)|x=1 = − 10
Maximum value = 1 − 5 + 5 − 1 = 0

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 49

 Calculus

f"(x)|x=3 = 90 > 0
Minimum value = 35 − 5.34 + 5.33 − 1 = −28
f"(x)|x=0 = 0
f′′′(x) = 60x 2 − 120x + 30
f′′′(x)|x=0 = 30 ≠ 0
Hence, neither maxima, nor minima at point x = 0

Example: Find the maxima and minima of

f(x) = x 3 − 3x 2 + 6x − 2 , in interval [−1, 1]
Solution: f′(x) = 3x 2 − 6x + 6
f ′ (x) = 0, ⇒ x 2 − 2x + 2 = 0
2 ± √4 − 8 + 2 ± 2 i
x= = =1+i
2 2
Hence f ′ (x) > 0 for − ∞ < x < ∞ : Monotonous function

Integration
b
Reverse process of differentiation or the process of summation ∫a f(x)dx defines the integral of any
continuous function.

Standard Integral Results

xn+1
1. ∫ x n dx = , n ≠ −1
n+1
1
2. ∫ x dx = log x
3. ∫ ex dx = ex
ax
4. ∫ ax dx =
log ea
5. ∫ cos x dx = sin x
6. ∫ sin x dx = −cos x
7. ∫ sec 2 x dx = tan x
8. ∫ cosec 2 x dx = −cot x
9. ∫ sec x tan x dx = sec x
10. ∫ cosec x cot x dx = −cosec x
1 x
11. ∫ 2 2 dx = sin−1 a
√a −x
1 1 x
12. ∫ 2 2 dx = a
sec −1 a
x√x −a
1 −1
13. ∫ 2 dx = sec x
x√x −1
14. ∫ cosh x dx = sinh x
15. ∫ sinh x dx = cosh x
16. ∫ sech2 x dx = tanh x
17. ∫ cosech2 x dx = −coth x
18. ∫ sech x tanh x dx = −sech x
19. ∫ cosech x cot h x dx = −cosech x
20. ∫ tan x dx = log sec x

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 50

 Calculus

21. ∫ cot x dx = log sin x

22. ∫ sec x dx = log( sec x + tan x) = log tan(π⁄4 + x⁄2)
x
23. ∫ cosec x dx = log(cosec x − cot x) = log tan 2
1 x
24. ∫ 2 2 dx = log(x + √x 2 − a2 ) = cosh−1 ( )
√x −a a
1 x
25. ∫ 2 2 dx = log(x + √x 2 + a2 ) = sinh−1 (a)
√a +x
a2 x x√a2 −x2
26. ∫ √a2 − x 2 dx = sin−1 +
2 a 2
x a 2
27. ∫ √a2 + x 2 dx = 2 √x 2 + a2 + 2 log(x + √x 2 + a2 )
x a2
28. ∫ √x 2 − a2 dx = 2 √x 2 − a2 − 2 log(x + √x 2 − a2 )
1 1 x
29. ∫ a2 +x2 dx = a tan−1 a
1 1 a+x
30. ∫ a2 −x2 dx = 2a log (a−x) where, x <a
1 1 x−a
31. ∫ x2 −a2 dx = 2a log ( x+a) where, x > a
x 1
32. ∫ sin2 x dx = 2 − 4 sin 2x
x 1
33. ∫ cos2 x dx = 2 + 4 sin 2x
2
34. ∫ tan x dx = tan x − x
35. ∫ cot 2 x dx = − cot x − x
36. ∫ ln x dx = x ln x − x
eax
37. ∫ eax sin bx dx = (a sin bx − b cos bx )
a2 +b2
eax
38. ∫ eax cos bx dx = a2 +b2
(a cos bx + b sin bx )
x [f(x) ′ (x)]dx x
39. ∫ e + f = e f(x)

Method of Finding Integrals

(A) Integration by Inspection
(B) Integration by Transformation
(C) Integration by Substitution
(D) Integration by Parts

Integration by parts:
du
∫ u v dx = u ∫ v dx − ∫( ∫ v dx)dx
dx
Selection of u & v I L A T E
E

Inverse Circular
(E.g.: tan−1 x) Exponential
Logarithmic Algebraic Trigonometric

Note: Take that function as “u” which comes first in “ILATE”

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 51

 Calculus

Some Other Important Formulae

b 1 β 2
Area = ∫a y dx = ∫ r dθ
2 α
b 2 2π β
Volume = π ∫a y dx= 3 ∫α r 3 sin θ dθ
1 − cos 2x
sin2 x =
2
2
1 + cos 2x
cos x =
2
3 sin x − sin 3x
sin3 x =
4
3 cos x + cos 3x
cos3 x =
4

Example: ∫ sec x 0 tan x 0 dx = ?

π
𝐒𝐨𝐥𝐮𝐭𝐢𝐨𝐧: 10 =
180
π
x0 = x
180
πx
πx πx sec 180 180 πx
0 0
∫ sec x tan x dx = ∫ sec tan = π = sec
180 180 π 180
180

Example: ∫ sin−1 x dx = ∫ 1 sin−1 x dx

= ∫ sin−1 x 1 dx
1
= sin−1 x x − ∫ x dx
√1 − x 2
(− dz⁄2)
= x sin−1 x − ∫ × (z = 1 – x 2 , dz = −2x dx )
√z
1/2
1 z
= x sin−1 x + ×
2 1/2
= x sin−1 x + (1 − x 2 )1/2

Rules for Definite Integral

b c b
1)∫a f(x)dx =∫a f(x)dx+∫c f(x)dx; a<c<b
b b a a
2) ∫a f(x)dx =∫a f(a + b − x)dx → ∫0 f(x)dx =∫0 f(a − x)dx
a a/2 a/2 a a/2
3) ∫0 f(x)dx =∫a f(x)dx+∫a
f(a − x)dx → ∫0 f(x)dx = 2 ∫a f(x)dx if f(a−x)=f(x)
=0 if f(a−x)= −f(x)
a a
4) ∫−a f(x)dx = 2 ∫0 f(x)dx if f(−x) = f(x), even function
=0 if f(x) = −f(x), odd function

1
1
𝐄𝐱𝐚𝐦𝐩𝐥𝐞: ∫ log ( − 1) dx =?
0 x
1 1
1 1−x
𝐒𝐨𝐥𝐮𝐭𝐢𝐨𝐧: Ι = ∫ log ( − 1) dx = ∫ log ( ) dx − − − − − − − − − − − − − − (1)
0 x 0 x

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 52

 Calculus

1 1
1 − (1 − x) x
Also, Ι = ∫ log ( ) dx = ∫ log ( ) dx − − − − − − − − − − − (2)
0 1−x 0 1−x
Add (1) & (2)
1 1 1 1
1−x x 1−x x
2 Ι = ∫ log ( ) dx + ∫ log ( ) dx = ∫ log ( ) dx = ∫ log(1)dx = 0
0 x 0 1−x 0 x 1−x 0

π
2 √sinx
𝐄𝐱𝐚𝐦𝐩𝐥𝐞: Ι = ∫ dx − − − − − − − − − − − − − − − − − − − − − − − (1)
√sinx + √cosx
0

π π π
√sin ( − x)
2 2 2 √cosx
Ι =∫ dx = ∫ dx − − − − − − − − (2)
0 π π 0 √cosx + √sinx
√sin ( − x) + √co s ( − x)
2 2
Add (1) & (2)
π π
π
2 √sinx + √cosx 2 π
2Ι = ∫ dx = ∫ 1 dx = x|02 =
0 √sinx + √cosx 0 2
π
Ι =
4

Improper Integral
b
Those integrals for which limit is infinite or integrand is infinite in a ≤ x ≤ b in case of ∫a f(x)dx ,
then it is called as improper integral.

Types of Improper Integral

i) The interval increases without limit
∞
(a) Let f(x) be bounded and integral is a ≤ x ≤ B, ∀ B >a. then ∫a f(x)dx is said to converge or
B ∞ B
to exist if limB→∞ ∫a f(x)dx exists finitely and ∫a f(x)dx = limB→∞ ∫a f(x)dx
(b) Let f(x) be bounded and integral in A ≤x ≤ b for every A<b.Then f(x) is said to converge or
b b b
to exist if limA→−∞ ∫A f(x)dx exists finitely and ∫−∞ f(x)dx = limA→−∞ ∫A f(x)dx
(c) Let f(x) be bounded and integral in A ≤ x ≤ a for every A<a and in a ≤x ≤B for every B>a.
∞ a B
Then ∫−∞ f(x)dx is said to be convergent if limA→∞ ∫A f(x)dx and limB→∞ ∫a f(x)dx exists
∞ a ∞ a B
finitely and we write ∫−∞ f(x)dx =∫−∞ f(x)dx + ∫a f(x)dx =limA→−∞ ∫A f(x)dx limB→∞ ∫a f(x)dx
ii)
(a) f(x) has infinite discontinuity only at the left end point, then
b b
∫a f(x)dx ⟹ limϵ→0+ ∫a+ϵ f(x)dx 0< ϵ < b − a
(b) f(x) has infinite discontinuity at the right end point then
b b−ϵ
∫a f(x)dx ⟹ limϵ→0+ ∫a f(x)dx 0< ϵ < b − a
(c) f(x) has infinite discontinuity at x=c, a<c<b then
b c−ϵ b
∫c f(x)dx ⟹ limϵ→0+ ∫a f(x)dx + limδ→0 ∫c+δ f(x)dx
If either of a or b does not exist then integral does not exist.

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 53

 Calculus

Note on Convergence
b
 ∫a f(x)dx is said to be convergent if the value of the integral is finite.
∞ ∞
 If (i) 0 ≤ f(x) ≤ g(x) for all x (ii) ∫a g(x)dx converges , then ∫a f(x)dx also converges
∞ ∞
 If (i) f(x) ≥ g(x) ≥ 0 for all x (ii) ∫a g(x)dx diverges, then ∫a f(x)dx also diverges
b b
 Assume both proper integrals ∫a f(x)dx and ∫a g(x)dx exist for each b≥a where f(x) ≥ 0 and
g(x) > 0 ∀ x ≥ a
f(x) ∞ ∞
If limx→∞ g(x) = c where c≠0, then both integrals ∫a f(x)dx and ∫a g(x)dx converge or both
diverge
∞ dx
 ∫1 xp
is converges when p> 1 and diverges when p≤ 1
∞ −px b
 ∫a e dx and ∫−∞ epx dx is converges for any constant p> 0 and diverges for p≤ 0
b dx
 The integral ∫a (b−x)p is convergent if p< 1
b dx
 The integral ∫a is convergent if p< 1
(x−a)p

∞ 1
Example: ∫0 1+x2
dx =?
B 1
Solution: limB→∞ ∫0 1+x2 dx
= limB→∞ [tan−1 x]B0
=limB→∞ [tan−1 B − 0]
π
=limB→∞ tan−1 B = 2

∞ 0
2 2
𝐄𝐱𝐚𝐦𝐩𝐥𝐞: ∫ xex dx = ∫ x ex dx
−∞ −∞
0 B
x2 2
𝐒𝐨𝐥𝐮𝐭𝐢𝐨𝐧: = lim ∫ xe dx + lim ∫ xex dx
A→∞ A B→∞ 0
0 B
x2 x2
e e
= lim [ ] + lim [ ]
A→∞ 2 B→∞ 2
A 0
2
1 eA 1 2 1
= lim [ − ] + lim [ eB − ]
A→∞ 2 2 B→∞ 2 2
= ∞ +∞ =∞
Thus integral diverges

3
dx
𝐄𝐱𝐚𝐦𝐩𝐥𝐞: Evaluate ∫ dx if it converges
√9 − x 2
0
Solution: The integral becomes infinite at x=3 (second type improper integral)
3−t
dx x 3−t 3−t
∫ = sin−1 ( )| = sin−1 ( )
0 √9 − x 2 3 0 3
3 π
As t → 0 = sin−1 ( ) = sin−1(1) =
3 2

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 54

 Calculus

Vector Calculus
Scalar Point Function
If corresponding to each point P of region R there is a corresponding scalar ϕ(P) is said to be a
scalar point function for the region R.
ϕ(P)= ϕ(x, y, z)

Vector Point Function

If corresponding to each point P of region R, there corresponds a vector defined by F(P) then F is
called a vector point function for region R.
F(P) = F(x, y, z) = f1(x, y, z)î +f2(x, y, z)ĵ +f3(x, y, z)k̂

∂ ∂ ∂
Vector Differential Operator or Del Operator: ∇ = (î ∂x
+ ĵ ∂y
+ k̂ ∂z
)

Gradient
The vector function ∇f is defined as the gradient of the scalar point function f(x,y,z) and written as
grad f.
∂f ∂f ∂f
Grad f = ∇f = î + ĵ + k̂
∂x ∂y ∂z
 ∇f is vector function
 If f(x,y,z) = 0 is any surface, then ∇f is a vector normal to the surface f and has a magnitude
equal to rate of change of f along this normal

Directional Derivative
⃗⃗ is the resolved part of ∇f in direction N
The directional derivative of f in a direction N ⃗⃗ .
⃗⃗
N
̂ where, N
∇f N ̂=
⃗⃗ |
|N
Where, ⃗N
⃗ is a unit vector in a particular direction.
 Directional derivative of f(x, y, z) is maximum along ∇f and magnitudeof this maximum is |∇f|.

Divergence
The divergence of a continuously differentiable vector point function F is denoted by div. F and is
defined by the equation.
div. F = ∇ . F
F = f î + ϕĵ + Ψk̂
div .F= ∇. F
∂ ∂ ∂
= (î + ĵ + k̂ ) . (f î + ϕĵ + Ψk̂)
∂x ∂y ∂z
∂f ∂ϕ ∂Ψ
= + +
∂x ∂y ∂z
 ∇. F is scalar
⃗
∂2 ∂2 ∂2
 Laplacian operator ∇2 = + +
∂x2 ∂y2 ∂z2
∇2 ϕ = ∇. (∇ϕ) = divgrad ϕ

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 55

 Calculus

Curl
The curl of a continuously differentiable vector point function F is denoted by curl F and is defined
by the equation.
î ĵ k̂
∂ ∂ ∂
Curl F = ∇ × F = |∂x ∂y
|
∂z
f ϕ Ψ
∇ × F is vector function

Solenoidal Vector Function

If ∇ A = 0, then A is called as solenoidal vector function.
Irrotational Vector Function
If ∇ × A =0, then A is said to be irrotational otherwise rotational.

DEL Applied Twice to Point Functions

∂2 f ∂2 f ∂2 f
1) div. grad f = ∇2 f= ∂x2 + ∂y2 + ∂z2 ---------- This is Laplace equation
2) curl grad f = ∇ × ∇f = 0
3) div. curl F = ∇. ∇ × F =0
4) curl (curl F) = ∇ × (∇ × F) = ∇(∇. F) − ∇2 F
5) grad (div F) = ∇(∇. F)= ∇ × (∇ × F) + ∇2 F

Vector Identities
f, g are scalar functions & F, G are Vector functions
1) ∇(f + g) = ∇f + ∇g
2) ∇. (F + G) = ∇. F + ∇. G
3) ∇ × (F + G) = ∇ × F + ∇ × G
4) ∇(fg) = f ∇g + g∇f
5) ∇. (fG)= ∇f. G + f∇. G
6) ∇ × (fG) = ∇f × G + f ∇ × G
7) ∇(F. G) = F × (∇ × G) + G × (∇ × F)
8) ∇. (F × G) = G. ( ∇ × F) − F. (∇ × G)
9) ∇ × (F × G) = F(∇. G) − G(∇. F)

Note:
1) ∇(f/g)= (g ∇f – f ∇g)/g 2
2) (F. G)′ = F ′ . G + F. G′
3) (F × G)′ = F ′ × G + F × G′
4) ∇2 (fg) = g ∇2 f + 2 ∇f. ∇g + f ∇2 g

Vector Product
1) Dot product of A × B with C is called scalar triplet product and denoted as [ABC]
Rule: For evaluating the scalar triplet product
(i) Independent of position of dot and cross
(ii) Dependent on the cyclic order of the vector

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 56

 Calculus

[ABC] = A × B. C = A . B × C
= B × C. A = B . C × A
= C × A. B = C. A× B
A × B. C = −(B × A. C)
⃗ × ⃗B) × ⃗C = (extreme × adjacent) × Outer
2) (A
= (Outer extreme) adjacent − (Outer adjacent) extreme
⃗⃗⃗ ⃗⃗⃗⃗
 (A × B) × ⃗C = (C ⃗ . ⃗A ) ⃗B − (C
⃗ . ⃗B ) ⃗A
 A ⃗ × (B ⃗ ×C ⃗ ) = (A⃗ .C
⃗ )B ⃗ − (A ⃗. B
⃗ )C ⃗
 (A ⃗ × B ⃗ )×C ⃗ ≠A ⃗ × (B ⃗ ×C ⃗ )

Example: Find unit vector normal to the surface xy 3 z 2 = 4 at point ( −1 , −1 ,2 )

∂ ∂ ∂
Solution: Normal vector = i (xy 3 z 2 ) + j (xy 3 z 2 ) + ⃗k (xy 3 z 2 )
∂x ∂y ∂z
3 2 3 2)
= grad(xy z ) = ∇(xy z
⃗
= y 3 z 2 i + 3xy 2 z 2 j + 2xy 3 zk
At point (−1, −1,2) = −4 i − 12j + 4k ⃗
−4i − 12j + 4k ⃗ 1
Vector = =− (i + 3j − ⃗k)
2
√4 + 12 + 42 2 √11

Example: Find directional derivatives of f(x, y, z) =xy 2 + yz 3 at the point (2 , −1 , 1)in the direction
⃗
of vector i + 2j + 2k
⃗ (3yz 2 )
Solution: ∇ f = i(y 2 ) + j (2xy + z 3 ) + k
= i − 3j − 3k ⃗ at (2 , −1, 1)
Directional derivation of f in the direction of i + y ⃗
⃗ +2k
⃗ + 2j + k
(1 ⃗) 1−6−6 11
⃗ − 3j − 3k
= (1 ⃗)× = =−
√12 + 22 + 23 3 3

Line Integral, Surface Integral & Volume Integral

 Line integral = ∫c F(R)dR
If F(R )=î f(x,y,z) + ĵ ϕ(x,y,z) + k̂ Ψ(x,y,z)
dR = î dx + ĵ dy + k̂ dz
∫c F(R )dR = ∫c( f dx + ϕ dy + Ψ dz )
 Surface integral: ∫s F ⃗⃗⃗⃗ or ∫ F
⃗ ds
s
⃗ N
⃗⃗ ds, Where N is unit outward normal to Surface.
 Volume integral: ∫v F dv
If F(R ) = f(x,y,z)î + ϕ (x,y,z)ĵ + Ψ (x,y,z) k̂ and δv = δxδyδz , then
∫ F dv = î∫ ∫ ∫ fdxdydz + ĵ ∫ ∫ ∫ ϕ dxdydz +k̂ ∫ ∫ ∫ Ψdxdydz

Example: If F=3xy î −y 2 ĵ, evaluate ∫c F dR Where c is the curve in the xy plane y = 2x 2 from (0,0) to
(1, 2).
Solution: Since the particle moves in the xy plane (z=0), we take R= x î + yĵ .Then,
∫c F. dr =∫c(3xydx − y 2 dy)
c is y=2x 2 , x goes from 0 to 1

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 57

 Calculus

1 1 1
x4 x5
∫ (6x 3 − 4x 4 )dx
= 6( ) − 4( )
0 4 0 5 0
6 4 30 − 16 14 7
= − = = =
4 5 20 20 10

Green’s Theorem
If R be a closed region in the xy plane bounded by a simple closed curve c and if P and Q are
continuous functions of x and y having continuous derivative in R, then according to Green’s
theorem,
∂Q ∂P
∮c(P dx + Q dy) = ∫R ∫ ( ∂x − ∂y
) dxdy

Stoke’s Theorem
If F be continuously differentiable vector function in R, then ∮ F dr = ∫ ∇ × F N ds

Gauss Divergence Theorem

The normal surface integral of a vector point function F which is continuously differentiable over
the boundary of a closed region is equal to the
∫ F. N. ds = ∫ div F dv
s v

Problems on Surface Integral

Example: ∬s ⃗F. n ⃗ S is surface of a cube bounded by
⃗ . ds where ⃗F = 4xz i − y 2 j + yzk
x = 0, x = 2
y = 0, y = 2
z = 0, z = 2
Solution: By divergence theorem

∬ ⃗F. n
⃗ . ds = ∬ div . ⃗Fdv
s v
∂ ∂ ∂
= ∫ (4xz) + (−y 2) + (yz)
∂x ∂y ∂z
v

= ∫ (4z − 2y + y) dv
v
2 2 2
= ∭(4z − y)dv = ∫ ∫ ∫ (4z − y)dz dy dx
0 0 0
2 2 2 2

= ∫ ∫(2z − 2
yz)|20 dy dx = ∫ ∫(8 − 2y)dy dx
0 0 0 0
2

= ∫(8y − y 2 )|2y=0 dx = ∫(16 − 4)dx

0
2
= ∫0 12dx = 12 × 2 = 24

info@thegateacademy.com ©Copyright reserved.Web:www.thegateacademy.com 58