Angle Measures

 Can either be in radians or in degrees. Although both can be used to define an angle, radians are more natural
in measurement since it is directly involved with the unit circle, with a radius of 1.
 The radian measure of an angle is the arc length of the associated arc on the unit circle.
 360˚ = 2π rad
180°
 Radians to Degrees: θπ× =θ˚
π
π
 Degrees to Radians: θ˚× =θπ
180°
Unit Circle
QI   QII   QIII   QIV  

Degrees Radians Degrees Radians Degrees Radians Degrees Radians

    180 Π = 6π/6 = 4π/4 = 3π/3     360 2π = 12π/6 = 8π/4 =

6π/3

30 π/6 150 5π/6 210 7π/6 330 11π/6

45 π/4 135 3π/4 225 5π/4 315 7π/4

60 π/3 = 2π/6 120 2π/3 = 4π/6 240 4π/3 = 8π/6 300 5π/3 = 10π/6

90 π/2 = 2π/6 = 2π/4     270 3π/2 = 6π/4 = 9π/6    

Six Trigonometric Identities (SohCahToa)
Sinθ = y Cscθ = 1/y
Cosθ = x Secθ = 1/x
Tanθ = Sinθ/Cosθ = y/x Cotθ = Cscθ/Secθ = x/y
Trigonometric Values
  sin cos tan

0 0 1 0

30 1/2 √ 3/2 √ 3/3

60 √ 3/2 1/2 √3
90 1 0 und
Pythagorean Identities
 Sin2θ +  1+  1+
Cos2θ = 1 Tan2θ = Sec2θ Cot2θ = Csc2θ
 
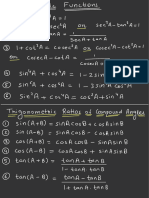
Addition and Subtraction Formulas
sin(A+B) = sinAcosB + sinBcosA   sin(A-B) = sinAcosB - sinBcosA
cos(A+B) = cosAcosB - sinAsinB   cos(A-B) = cosAcosB + sinAsinB
tanA +tanB   tanA−tanB
tan(A+B) = tan(A-B) =
1−tanAtanB 1+ tanAtanB
Product-to-Sum Identities
1
cosAcosB= [cos ( A+ B )+ cos ( A−B ) ]
2
−1
sinAsinB= [cos ( A +B )−cos ( A−B ) ]
2
1
sinAcosB= [ sin ( A + B ) +sin ( A−B ) ]
2
1
cosAsinB= [sin ( A+ B )−sin ( A−B ) ]
2
Sum-to-Product Identities

cosA +cosB=2 cos ( A +B

2 ) cos (
A−B
2 )

A +B A−B
cosA −cosB=−2 sin ( ) sin (
2 2 )

A +B A−B
sinA +sinB =2sin ( ) cos (
2 2 )

A+ B A−B
sinA−sinB=2 cos (
2 ) ( 2 )
sin

Double Angle Identities

sin(2A) = 2sinAcosA

cos(2A) = cos2A - sin2A = 2cos2A -1 = 1 - sin2A

2tanA
tan(2A) =
1−tan 2 A
Half Angle Identities

A 1+cosA
cos
2
=±
√2
A 1−cosA
sin
2
=±
√2
A 1−cosA sinA 1−cosA
tan
2
=±
√ =
1+ cosA 1+cosA
Graphs of Periodic Functions - Repeating at every period
=
sinA

 Sine Graph [y = A sin B(x + a)+c]

o Odd function; sin(-x) = -sin(x)
o The period of a sine function is defined as 2π / B
 Cosine Graph [y = A cos B(x + a)+c]
o Even function; cos(-x) = cos(x)
o The period of a cosine function is defined as 2π / B
 GRAPHING SINE OR COSINE FUNCTIONS
o The "A" in the function is the amplitude that determines the range of the periodic graph
o Solve the period. From 0 to 2π / B, divide it into 4 equal parts (by midpoint formula)
o Plot. Shift the graph if necessary.
 Tangent Graph [y = A tan B(x + a)+c]
o Odd function; tan(-x) = -tan(x)
o The boundaries of a tangent function is defined by -π / 2B and π / 2B
o Therefore, the vertical asymptotes are at the boundaries.
 Cotangent Graph [y = A cot B(x + a)+c]
o Odd function; cot(-x) = -cot(x)
o The boundaries of a cotangent function is defined by 0 and π / B
o Therefore, the vertical asymptotes are at the boundaries.
 GRAPHING TANGENT AND COTANGENT FUNCTIONS
o The "A" in the function is the amplitude that determines the range of the periodic graph
o Solve the asymptotes. Between each boundaries, divide it into 4 equal parts (by midpoint formula).
The boundaries are the vertical asymptotes.
o Plot. Shift the graph if necessary.
 Secant Graph [y = A sec B(x + a)+c]
o Even function; sec(-x) = sec(x)
o Reciprocal of the cosine function
 Cosecant Graph [y = A csc B(x + a)+c]
o Odd function; csc(-x) = -csc(x)
 o Reciprocal of the sine function
 GRAPHING SECANT AND COSECANT FUNCTIONS
o Since both are reciprocals of sine and cosine, you must base the following graphs to the sine and
cosine graphs. The figure of these two are like repeating parabolas wherein the vertices are aligned to
the multiple crests and troughs of sine and cosine graphs.
o The vertical asymptotes of the secant and cosecant graphs are aligned at the x-intercepts of sine and
cosine graphs.