CE 332

GEOTECHNICAL ENGINEERING I

Lecture 2: Stress changes within a soil due to application

of an external load & Compression and Consolidation
Mrs Honoria Homu-Hedziga
Room 116
Stress due to an external load

• So far, you have calculated stresses in the soil due to self-

weight and seepage
• However, one of the key functions of a soil layer is to
support the structures that are founded on it
• It is therefore necessary to obtain an estimate of change in
soil stresses due to external loads imposed by structures
• There are two main reasons for obtaining the estimate of
change in soil stresses:
1) To ensure that the soil is not approaching failure due to
the loads imposed by the structure, and
2) To estimate the amount of settlement that the structure
may experience during its life span
Stress due to an external load

•Geotechnical engineers must design foundations, retaining

walls and other soil constructions which will not collapse
(safe) and do not deform excessively under working
conditions.
•Soil is not an elastic material, but is treated as one for the
purpose of calculating increases in stress and settlements
resulting from surface loads such as shallow foundations.
•Soil in the field is typically subjected to total normal stresses
in the vertical (z) and horizontal (x) directions due to self
weight of the soil and any applied external loading (e.g., from
a foundation)
Soil elasticity

•Settlements calculated using elasticity methods depend on

the elastic parameters used to characterise the soil –
particularly the stiffness modulus. The stiffness modulus
depends on the stress history and the stress state of the soil, as
on the applied stress path.
•Applying a surface load causes an immediate increase in
total stress, and a gradual increase in effective stress when the
pore water pressures have returned to their equilibrium values.
•If the soil beneath a foundation is a clay, settlements will
develop over time as the excess pore water pressures generated
by the application of the load dissipate and clay consolidates.
•Elasticity calculations may be used to estimate either the
initial (undrained) or the long-term (fully drained) soil
movements
Soil elasticity

• To estimate the immediate (undrained) soil movements, the

elastic parameters  (Young’s modulus) and  (Poisson’s ratio)
must be obtained from undrained tests and defined in terms of
total stress. Subscript (u) indicates undrained or total stresses
•To estimate long-term (drained) soil movements, the  and 
must be obtained from drained tests and defined in terms of
effective stresses. Prime (‘) is used to indicate effective stress
parameters
•Soils are non-homogenous and display anisotropy (i.e., have
different values of a given property in different directions, and
have non-linear stress-strain relationships which are
dependent on stress history and the stress path followed.
Stress-Strain Response of Soil
• Estimation of change in stress is not enough for the
calculation of maximum stress a soil can sustain or the
calculation of its settlement
• A stress-strain response for the soil is necessary
• Such a response can be obtained by conducting
• Laboratory tests on undisturbed soil samples
• Field or in-situ tests
• As we can see from the figure
on the right, the stress-strain
curve for soils in non-linear
• In addition, soils are non-
homogenous, anisotropic and
undergo irreversible volume
change
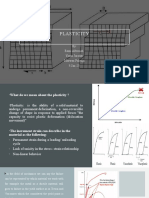
Idealized Stress-Strain Response
•It is impossible to take into account all aspects of soil
behaviour in a conceptual stress-strain response and some
idealization is necessary as shown below:
Linear elastic behaviour

• For analysis, an idealisation of the stress-strain relationship

is used for simplicity of calculations.
One idealisation is shown by
the dotted lines, linearly elastic
behaviour (i.e. Hooke’s Law) is
assumed between O and Y’
(assumed yield point) followed
by unrestricted plastic strain
Y’P at constant stress
Linear elastic behaviour

•As shown in the figure above, a linear elastic model is

adequate for settlement calculations
Linear Elastic Model - Parameters

•The linear elastic model is used to describe materials which

respond as follows:
i. The strains in the material are small (linear)
ii. The stress is proportional to the strain (  ) (linear)
iii. The material returns to its original shape when the
loads are removed, and the unloading path is the same
as the loading path (elastic)
iv. There is no dependence on the rate of loading or
straining (elastic)
Linear Elastic Model - Parameters

• A linear elastic model

requires the stiffness of the
soil for the calculation of
settlements from the change
in stress
• The stiffness of the soil is
represented by the elastic
modulus of the soil, i.e. The
slope of the stress-strain
curve as shown in the figure
on the right
Elastic-perfectly plastic behaviour

• The image below shows elastic-perfectly plastic model of

material behaviour.
•For stability calculations that
involve taking the soil to
failure, a perfectly plastic
model is required
•If only the failure of soil in a
practical problem is of
interest, then the elastic phase
can be omitted and the rigid
perfectly plastic model (on next
slide) may be used
Rigid-perfectly plastic behaviour

• The image below shows rigid-perfectly plastic model of

material behaviour.
Elastic-strain hardening behaviour

• Another idealisation is the elastic-strain hardening model in

which plastic strain beyond the yield point is necessary for
further stress increase (i.e., soil hardens or strengthens as it
strains).
A further idealisation is the
elastic-strain softening plastic model
shown by OY’P’ where the plastic
strain beyond yield point is
accompanied by stress decrease
or softening of the material
Elastic Modulus and Poisson’s Ratio

• If axial stress is plotted against axial strain, the elastic

modulus is the Young’s Modulus (E)
• If shear stress is plotted against shear strain, the elastic
modulus is the shear modulus (G)
• E is related to G using the Poisson’s ratio ()
Stresses in Soil due to Surface Loads

•To analyse problems such as compressibility of soils, bearing

capacity of foundations, stability of embankments, and lateral
pressure on earth retaining structures, we need to know the
nature of the distribution of stress along a given cross section
of the soil profile.
•The distribution of stresses within a soil layer due to the
application of a surface load is obtained by assuming that the
soil is a semi-infinite, homogenous, linear, isotropic elastic
material
•A semi-infinite mass is bounded on one side and extends
infinitely in all other directions
•A semi-infinite mass is often called elastic half-space
•For soils, the horizontal ground surface is the bounding side
Some questions for you...

•Why would engineers care about how soil deforms?

•What do you think might affect how much a soil deforms?
•How might the loads on a soil change?

•We build things on soil, we do not like when things rotate.

There’s a limit to how much deformation a structure can take
•Water content (void ratio, relative density), stresses applied to
it, type of soil, and temperature
•Geological processes
Compression and Consolidation
Compression and Consolidation
•~ 30cm per
year of
settlement
occurs in some
locations
around the
world
•What are the
causes of
settlement?

•Natural consolidation (soft clays settling after deposition

•Tectonic movements
•Extra load due to construction
•Draining of aquifers
Mechanisms for volume change in soils

•Changes in effective stress lead to compression

•If effective stress doesn’t change then there is no change in
volume due to compression
•Effective stress is carried by the solid particles of the soil
skeleton – therefore if there is not change in effective stress,
there will be no deformation
Mechanisms for volume change in soils: Shear

•Shear loading can cause the volume to increase (dilation) or

to decrease (contraction)
Deformation characteristics were wrongly calculated
Flooded during a typhoon
Building blocks: Elasticity

What do we need to remember from Materials

–Materials are commonly assumed to be isotropic and
homogeneous
–Normal stresses cause normal strains
–Shear stresses cause shear strains
•Strains are related to the applied stresses by the elastic
modulus

•Each element of soil strains according to its own stress and

strength characteristics
•Settlement at the surface is a culmination of settlement in all
layers