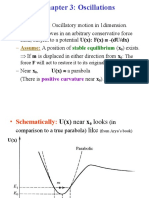
Forced vibration with hysteresis damping

 Consider a single degree of freedom with hysteresis damping and subjected to a harmonic
force F(t)= FoSin(ωt), as indicated in Fig (1) The equation of motion can be derived .

mX’’+(βk/ω)X’+kX = FoSin(ωt) >>>>>>>>>>>E.O.M Eq (1)

Fig (1)

 Where (βk/ω) X’ = (h/ω) X’ denotes the damping force. Although the solution of Eq (1) is
quite involved for a general forcing function F(t), our interest is to find the response under a
harmonic force.

The steady state solution of Eq (1) Can be assumed.

Xp(t) = X Sin (ωt – ϕ) Eq (2)

By substituting Eq (2) into Eq (1) we obtain

X = Fo/ k [(1-ω2/ωn2)2 + β2 ]1/2 >>>>>> The response Eq (3)

And The phase angle ( ϕ ) can be found

Φ = tan-1[ β/(1-ω2/ωn2)] Eq (4)

Example :-

A load of 5000 N resulted in a static displacement of 0.05 m in a composite structure. A

harmonic force of amplitude 1000 N is found to cause a resonant amplitude of 0.1 m. Find

(a) the hysteresis-damping constant of the structure.

(b) the energy dissipated per cycle at resonance.

(c) the steady-state amplitude at one-quarter of the resonant frequency.

(d) the steady-state amplitude at thrice the resonant frequency.

Solution

(a) K=W/δst = 5000/0.05 = 105 N/m

When ω = ωn

X = Fo / kβ → 0.1 = 1000/105β → β = 0.1

(b) ΔW= πCeqωx2 = πβkx2 ,where Ceq = βk/ω

ΔW= (0.1)(105)(0.1)2 = 314.16 joules / cycle

(c) Steady-state amplitude at one-quarter of the resonant frequency : ω/ωn = 0.25

X = Fo/ k [(1-ω2/ωn2)2 + β2 ]1/2

X = 1000/ 105 [(1-0.252)2 + (0.1)2 ]1/2 = 0.01061 m

(d) Steady-state amplitude at thrice the resonant frequency : ω/ωn = 3

X = 1000/ 105 [(1-32)2 + (0.1)2 ]1/2 = 0.00125 m