DM Recurrence Relation

Recurrence Relation and it Applications
Dr. Tarkeshwar Singh

Department of Mathematics
November 2, 2020
Recurrence Relations
Types of Recurrence Relations
Solution of Recurrence Relations
Generating Functions
Outline
Types of recurrence relations
Non-linear Recurrences.
Dr. Tarkeshwar Singh Recurrence Relation and it Applications

A recursive definition of a set S consists of three clauses:

The basis clause explicitly lists at least one primitive element
in S, ensuring that S is nonempty.
The recursive clause establishes a systematic recipe to
generate new elements from known elements.
The terminal clause guarantees that the first two clauses are
the only ways the elements of S can be obtained.(The
terminal clause is generally omitted for convenience).

Recursive Functions
Let a ∈ W and X = {a, a + 1, a + 2, . . . }. The recursive definition
of a function f with domain X consists of three parts, where k > 1.
Basis clause: A few initial values of the function
f (a), f (a + 1), . . . , f (a + k − 1) are specified.
An equation that specifies such initial values is an initial
condition.
Recursive clause: A formula to compute f (n) from the k
preceding functional values f (n − 1), f (n − 2), . . . , f (n − k) is
made.
Such a formula is a recurrence relation (or recursion formula).
Terminal clause: Only values thus obtained are valid
functional values. (For convenience, we drop this clause from
our recursive definition.)

Recurrence equations
Definition
A recurrence equation (or recurrence relations) is any equation
that can be used to specify an infinite sequence < Xn > n ∈ N by
expressing Xn in terms of Xn−1 , Xn−2 , . . . , X1 , X0 and n.

Tower of Brahma
Example
Tower of Hanoi: According to a legend of India, at the beginning
of creation, God stacked 64 golden disks on one of three diamond
pegs on a brass platform in the temple of Brahma at Benares

The handshake problem

Example
There are n guests at a sesquicentennial ball. Each person shakes
hands with everybody else exactly once. Define recursively the
number of handshakes h(n) that occur.

Fibonacci Sequence
Example
Leonardo Fibonacci, the most outstanding Italian mathematician
of the Middle Ages, proposed the following problem around 1202:
Suppose there are two newborn rabbits, one male and the other
female. Find the number of rabbits produced in a year if:
(a). Each pair takes one month to become mature.
(b) Each pair produces a mixed pair every month, from the second
month.
(c) No rabbits die.

Illustration
Example
Imagine n lines in a plane such that no two lines are parallel, and
no three are concurrent. Let fn denote the number of distinct
regions into which the plane is divided by them. Define fn
recursively.

Pizza Problem
Example
Let fn denote the maximum number of places into which a pizza
can be divided with n cuts. Find a formula for fn .

Triangulation of convex polygons

Example
The nth Catalan number Cn denotes the number of ways to divide
a convex (n + 2)-gon into triangles by drawing nonintersecting
diagonals.

Order of Recurrence Relation

Definition
A recurrence equation of order k is one of the form
Xn = g (n, Xn−1 , Xn−2 , . . . , Xn−k ) where g is a functions of k + 1
variables.

Linear Recurrence Relation with Constt. Coeff.
Definition
A linear recurrence equation of order k is one which can be written
as Xn + p1 (n)Xn−1 + p2 (n)Xn−2 + · · · + pk (n)Xn−k = q(n).
Where, p1 (n), p2 (n), . . . , pk (n), &q(n) are functions of n only.
If we replace n by n + k, we can write this linear recurrence

equation in the alternative form:
Xn+k + ak−1 (n)Xn+k−1 + · · · + a0 (n)Xn = q 0 (n).
If all pi (n) are constant ∀i, 1 ≤ i ≤ n, then the above recurrence

relation is known as Linear recurrence relation with constant
coefficients(LRRWCC).
LRRWCC
The LRRWCC is written as

Xn + a1 Xn−1 + a2 Xn−2 + · · · + ak Xn−k = q(n).
If q(n) = 0, then above LRRWCC is known and Linear
Homogeneous Recurrence Realtaion with Constant
Coefficients (LHRRWCC).
If q(n) 6= 0, then above LRRWCC is known and Linear
Non-homogeneous Recurrence Realtaion with Constant
Coefficients (LNHRRWCC).
Solution of the above recurrence relation is nothing but as
sequence < an > which satisfy the above recurrence relation.

Characteristic Root Method
Solution of LHRRWCC
Definition
We define an operator E on a sequence < Xn > where n ∈ N by
E (< Xn >) =< Xn+1 > and
E 2 (< Xn >) = E (< Xn+1 >) =< Xn+2 >. Where E 0 = I the
identity operator such that I (< Xn >) =< Xn >.

Solution of LHRRWCC
Theorem
Let < an > and < bn > be the solutions of the LHRRWCC
L(E )(Xn ) = 0, then an + bn and kan are also solutions of
L(E )(Xn ) = 0.

Solution of LHRRWCC
Example
Find the solution of Xn+1 − 3Xn = 0 for all n ≥ 0 with X0 = 4.

Iterative Method
Solving the recurrence relation for a function f means finding an

explicit formula for f (n) . The iterative method of solving it
involves two steps:
Apply the recurrence formula iteratively and look for a pattern
to predict an explicit formula.
Use induction to prove that the formula does indeed hold for
every possible value of the integer n.
More generally, using iteration we can solve the recurrence relation

an = an−1 + f (n).


Let L(Xn ) = 0 be a linear homogeneous recurrence relation with
constant coefficients (LHRRWCC). Then we must have
L(E ) = E k + ak E k−1 + · · · + a1 E + a0 I = 0.
Theorem
Let L(Xn ) = 0 be a linear homogeneous recurrence relation with
constant coefficients (LHRRWCC). If
L(E ) = (E − α1 I )(E − α2 I ) . . . (E − αk I ) and all αi are distinct,
P general solution of L(E ) = 0 is given by
then the
Xn = ki=1 Ai αi n . Where Ai are known as arbitrary constants.

Suppose we have LHRRWCC is written as

Xn + a1 Xn−1 + a2 Xn−2 + · · · + ak Xn−k = 0. To find the solution
we have to follow the following steps:
We assume the solution Xn = αn and substitute it in above
LHRRWCC.
We have then αn + a1 αn−1 + · · · + ak = 0.
The above equation is known as characteristic equation of
LHRRWCC.
If all the roots of the above equations are distinct then the
solution is of the type Xn = ki=1 Ai αi n . Where Ai are known
P
as arbitrary constants.


Theorem
The general solution of (E − αI )n (Xn ) = 0 is given by
Xn = (A0 + nA1 + n2 A2 + · · · + nn−1 An−1 )αn , where
A0 , A1 , . . . , An−1 are arbitrary constant.

LNHRRWCC
The LNHRRWCC is written as

Xn + a1 Xn−1 + a2 Xn−2 + · · · + ak Xn−k = q(n).
First, we consider LHRRWCC as
Xn + a1 Xn−1 + a2 Xn−2 + · · · + ak Xn−k = 0 and let the
(h)
solution is Xn .
(h) (p) (p)
Then the general solution is Xn = Xn + Xn , where Xn is
known as particular solution of the LNHRRWCC.

Illustration
Example
Find the general solution of the LNHRRWCC, an+1 − 3an = 4(5)n .

Particular Solutions
There are no general procedure for finding the particular
solution of a recurrence relation.
However for certain function q(n) such as polynomial in n and
Power of constant r n is known.
If q(n) is a sine or cosine functions of n then we can find the
particular solutions.

LNHRRWCC
Theorem
If q(n) = (b0 + b1 n + b2 n2 + · · · + br nr )αn and α is not a root of
the auxiliary equation then the recurrence relation has a particular
solution of the form Xnp = (B0 + B1 n + B2 n2 + · · · + Br nr )αn .
Theorem
If q(n) = (b0 + b1 n + b2 n2 + · · · + br nr )αn and α is a root of the
auxiliary equation with multiplicity m then the recurrence relation
has a particular solution of the form
Xnp = (B0 + B1 n + B2 n2 + · · · + Br nr )nm αn .

Generating functions provide a powerful tool for solving
LHRRWCCs.
Generating Functions were invented in 1718 by the French
mathematician Abraham De Moivre.
Generating functions can also solve combinatorial problems.
Example
6
−1
f (x) = xx−1 = 1 + x + x 2 + x 3 + x 4 + x 5 . is known as generating
function of the sequence of coefficients 1, 1, 1, 1, 1, 1 in the
polynomial.

Definition
Let a0 , al , a2 , . . . , be a sequence of real numbers. Then the
function g (x) = ao + a1 x + a2 x 2 + · · · + an x n is the generating
function for the sequence {an }.
Generating functions for the finite sequence a0 , a1 , . . . , an can also

be defined by letting ai = 0 for i > n; thus
g (x) = ao + a1 x + a2 x 2 + · · · + an x n is the generating function for
the finite sequence a0 , a1 , . . . , an .

Example
Using generating functions, solve the recurrence relation
an = 6an−1 − 9an−2 , where a0 = 2 and a1 = 3.
Example
Using generating functions, solve the Fibonacci recurrence relation
Fn = Fn−1 + Fn−2 , where F1 = 1 = F2 .
Example
Use the method of generating function to solve
an+1 − 8an + 16an−1 = 4n , where n ≥ 1; a0 = 1, a1 = 8.

Method of Telescoping Sums

This method is useful to solve recurrence relations of the form:
an = an−1 + g (n), particularly if kn=1 g (n) is easy to find.
P
Example
Solve the recurrence relation an − an−1 = Fn+2 Fn−1 n ≥ 1, where
a0 = 2 and Fn is the nth Fibonacci number.

Telescoping Sums
Example
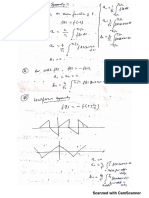
Solve the recurrence relation an = n3 an−1 , n ≥ 1, where a0 = 2.

Useful Method
To obtain a solution of the recurrence relation

Xn = f (n)Xn−1 + g (n) where f (n) 6= 0, ∀n, then we have to follow
the following steps:
Find the solution {Xn } for the homogeneous part of the
recurrence relation, so Xn = f (n)Xn−1 , ∀n ≥ 1.
Assume that the solution of the given recurrence relation if of
the form un = Xn bn .
Xn bn = f (n)Xn−1 bn−1 + g (n).
Xn bn = f (n)Xn bn−1 + g (n).
Therefore bn = bn−1 g (n)/Xn .
After find bn we can calculate un

Substitution Method
This method can be used to solve some non-linear recurrence
relations.
Example
Solve the recurrence relation an = an/2 + n for n = 2k , k ≥ 1 with
a1 = 0.
Example
√ √
Solve the recurrence relation xn = (2 xn−1 + 3 xn−2 )2 n ≥ 2 with
initial conditions x0 = 1, x1 = 4.
Example
7
xn−1
Solve the recurrence relation xn = 12
xn−2
with initial conditions
x0 = 1 and x1 = 2.

DM Recurrence Relation

Uploaded by

Document Information

Original Description:

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

DM Recurrence Relation

Uploaded by

Copyright:

Available Formats

Recurrence Relation and it Applications

Dr. Tarkeshwar Singh

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

A recursive definition of a set S consists of three clauses:

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

The handshake problem

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Triangulation of convex polygons

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Order of Recurrence Relation

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Linear Recurrence Relation with Constt. Coeff.

If we replace n by n + k, we can write this linear recurrence

Xn+k + ak−1 (n)Xn+k−1 + · · · + a0 (n)Xn = q 0 (n).

If all pi (n) are constant ∀i, 1 ≤ i ≤ n, then the above recurrence

The LRRWCC is written as

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Solving the recurrence relation for a function f means finding an

More generally, using iteration we can solve the recurrence relation

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Characteristic Root Method

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Characteristic Root Method

Suppose we have LHRRWCC is written as

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Characteristic Root Method

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

The LNHRRWCC is written as

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Generating functions for the finite sequence a0 , a1 , . . . , an can also

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Method of Telescoping Sums

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

To obtain a solution of the recurrence relation

Dr. Tarkeshwar Singh Recurrence Relation and it Applications

You might also like