AREAS ANTIDERIVATIVE:

𝑥 𝑛+1
The Area Problem 𝑥𝑛 =
𝑛+1
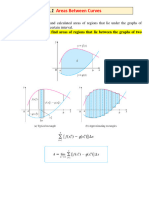
We begin by attempting to solve the area problem: find
the area of the region 𝑆 that lies under the curve 𝑦 = DEFINITE INTEGRAL PROPERTIES
𝑓(𝑥) from 𝑎 to 𝑏. This means that 𝑆, is bounded by the
graph of a continuous function 𝑓 [where 𝑓(𝑥) ≥ 0], The 𝑏

vertical lines 𝑥 = 𝑎 and 𝑥 = 𝑏. And the 𝑥-axis. ∫ 𝑓 (𝑥)𝑑𝑥 = 𝐹(𝑥)]𝑏 = 𝐹(𝑏) − 𝐹(𝑎)
𝑎 𝑎
Recall that in defining a tangent we first approximated 𝑏 𝑎
the slope of the tangent line by slopes of secant lines 1. ∫𝑎 𝑓 (𝑥)𝑑𝑥 = − ∫𝑏 𝑓(𝑥)𝑑𝑥
and then we took the limit of these approximates. We
𝑎
pursue similar ideas for areas. 2. ∫𝑎 𝑓 (𝑥)𝑑𝑥 = 0

We first approximate the region 𝑆 by rectangles and 𝑏 𝑐 𝑐

then we take the limit of the areas of these rectangles 3. ∫𝑎 𝑓 (𝑥)𝑑𝑥 + ∫𝑏 𝑓 (𝑥)𝑑𝑥 = ∫𝑎 𝑓(𝑥)𝑑𝑥
as we increase the number of rectangles.
𝑏
4. ∫𝑎 𝑐𝑑𝑥 = 𝑐(𝑏 − 𝑎)
EXAMPLE:
𝑏 𝑏
1. Use rectangles to estimate the area under 5. ∫𝑎 𝑐 𝑓 (𝑥)𝑑𝑥 = 𝑐 ∫𝑎 𝑓(𝑥)𝑑𝑥
the parabola 𝑦 = 𝑥 2 from 0 to 8
𝑏 𝑏
6. ∫𝑎 [𝑓(𝑥) ± 𝑔(𝑥)]𝑑𝑥 = ∫𝑎 𝑓(𝑥)𝑑𝑥 ±
Def. The AREA 𝐴 of the region 𝑆 that lies under the graph
of the continuous function 𝑓 is the limit of the sum of the 𝑏
areas of approximately rectangles: ∫𝑎 𝑔(𝑥)𝑑𝑥

𝐴 = lim 𝑅𝑛 = lim[𝑓 (𝑥1 )∆𝑥 + 𝑓(𝑥2 )∆𝑥 + ⋯ 𝑏

7. ∫𝑎 𝑓𝑥𝑑𝑥 > 0 𝑎𝑛𝑑 ∫𝑎 𝑓 (𝑥)𝑑𝑥 < 0
𝑏
𝑛→ 𝑛→
+ 𝑓 (𝑥𝑛 )∆𝑥]

Note: It can be shown that an equivalent definition of an

area is the following: 𝐴 is the unique number that is EXAMPLES:
smaller than all the upper sums and bigger than all the
lower sums. 1
1. ∫0 𝑥 2 𝑑𝑥
TRY! 8
2. Evaluate the upper sums and lower sums for 2. ∫0 𝑥 2 𝑑𝑥
𝑓 (𝑥) = 𝑥 2 , 0 ≤ 𝑥 ≤ 1 with 𝑛=
4, 8, 𝑎𝑛𝑑 10. Illustrate the diagrams. 2
3. ∫0 (𝑥 2 + 1)𝑑𝑥

4
4. ∫1 (2𝑥 2 + √𝑥)𝑑𝑥
3. Evaluate the midpoint, upper sums and
lower sums for 𝑓 (𝑥) = 𝑥 2 + 1, 0 ≤ 𝑥 ≤ 2 2 𝑥 5+2𝑥 3+1
5. ∫1 𝑑𝑥
with 𝑛 = 4 𝑎𝑛𝑑 8. Illustrate the diagrams. 𝑥2

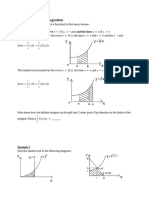
THE FUNDAMENTAL THEOREM OF CALCULUS

Def. If 𝑓 is continuous on [𝑎, 𝑏], then the function 𝐹

𝒙
defined by 𝑭(𝒙) = ∫𝒂 𝒇(𝒕)𝒅𝒕 , 𝑎 ≤ 𝑥 ≤ 𝑏 is continuous
on [𝑎, 𝑏] and differentiate on (𝑎, 𝑏), and 𝐹 ′(𝑥) = 𝑓(𝑥).
𝒃
Def. If 𝑓 is continuous on [𝑎, 𝑏], then ∫𝒂 𝒇(𝒙)𝒅𝒙 =
𝑭(𝒃) − 𝑭(𝒂) where 𝐹 is any antiderivative of 𝑓, that
is, a function 𝐹 such that 𝐹 ′ (𝑥) = 𝑓(𝑥)

DERIVATIVE:
𝑥 𝑛 = 𝑛𝑥 𝑛−1