Professional Documents
Culture Documents
The Process of Modeling Then Solving A Real Life Problem.: Example: Transportation, Allocation, Management
Uploaded by
Ali Mzayhem0 ratings0% found this document useful (0 votes)
24 views9 pagesThe document discusses modeling and solving real-world problems using operations research techniques. It provides the example of using linear programming to solve transportation and allocation problems by formulating an objective function and constraints as linear equations and inequalities. The optimal solution obtained minimizes or maximizes the objective function while satisfying all constraints.
Original Description:
Original Title
Lec 1 pdf
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentThe document discusses modeling and solving real-world problems using operations research techniques. It provides the example of using linear programming to solve transportation and allocation problems by formulating an objective function and constraints as linear equations and inequalities. The optimal solution obtained minimizes or maximizes the objective function while satisfying all constraints.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
24 views9 pagesThe Process of Modeling Then Solving A Real Life Problem.: Example: Transportation, Allocation, Management
Uploaded by
Ali MzayhemThe document discusses modeling and solving real-world problems using operations research techniques. It provides the example of using linear programming to solve transportation and allocation problems by formulating an objective function and constraints as linear equations and inequalities. The optimal solution obtained minimizes or maximizes the objective function while satisfying all constraints.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 9
The process of modeling then solving a real life problem.
Example: transportation, allocation, management.
The solution provided is optimal.
Dr. Houssein Alaeddine
f(x)
Global optimum
Local optimum
Local optimum
x Dr. Houssein Alaeddine
Formulation of problem
Objective function
Example: minimize the total travel time between origin-destination
Decision Variables
Example: vehicles, roads
Constraints
Example: capacity, velocity
Dr. Houssein Alaeddine
Photo by Denys Nevozhai on Unsplash.
https://towardsdatascience.com/what-is-operations-research-1541fb6f4963
Linear pogramming
A technique used to solve linear problems.
The objective function is expressed by a linear function.
The constraints are expressed by linear inequalities.
Dr. Houssein Alaeddine
Linear function
A function f ( x1 , x2 ,..., xm ) is linear if for some (c1 , c2 ,..., cm )
f ( x1 , x2 ,..., xm ) c1 x1 c2 x2 ... cm xm
Example
Linear function: f ( x, y ) x 2 y
Non-linear functions: f ( x, y ) x 2 y 2 , f ( x, y ) 2 xy
Dr. Houssein Alaeddine
Linear inequality
For any linear function f ( x1 , x2 ,..., xm ) and any number b
f ( x1 , x2 ,..., xm ) b and f ( x1 , x2 ,..., xm ) b are linear inequalities.
Example
x 2 y 10
2x y 4
Dr. Houssein Alaeddine
Formulation of a LPP
A Linear Programming Problem can be stated as follows:
Find x1 , x2 ,..., xm so that:
The objective function c1 x1 c2 x2 ... cm xm is maximal
subject to
a 1,1x1 a 1,2 x 2 ... a 1, j x j . . . a 1,m x m b1
.
.
a i,1x1 a i,2 x 2 ... a i, j x j . . . a i, m x m b i
.
.
a n,1x1 a n,2 x 2 ... a n, j x j . . . a n,m x m b n
Where ai , j , bi , c j are constants and x j are variables. Dr. Houssein Alaeddine
Example
Maximize 2 x1 x2
s.t.
2x1 x 2 8
x1 - 3x 2 2
Dr. Houssein Alaeddine
You might also like
- (Multivariable Calculus) : Dr. Adnan Jahangir and Ms. Nadia Rehman Online Classes Spring 2020Document28 pages(Multivariable Calculus) : Dr. Adnan Jahangir and Ms. Nadia Rehman Online Classes Spring 2020Šh AbdullahNo ratings yet
- B For I 1,, M: N J J JDocument19 pagesB For I 1,, M: N J J Jضيٍَِِ الكُمرNo ratings yet
- 09 - nlp1 - OnlineDocument23 pages09 - nlp1 - OnlineHuda LizamanNo ratings yet
- Additional ProblemsDocument6 pagesAdditional ProblemsAnonymous Q3EMYoWNSNo ratings yet
- FALLSEM2023-24 SWE1002 TH VL2023240103269 2023-10-25 Reference-Material-IIIDocument6 pagesFALLSEM2023-24 SWE1002 TH VL2023240103269 2023-10-25 Reference-Material-IIIKartik SoniNo ratings yet
- Module 3 - Lesson 3.3 Critical Points by Non-Linear FunctionDocument7 pagesModule 3 - Lesson 3.3 Critical Points by Non-Linear FunctionMaddyyyNo ratings yet
- Prob StatDocument46 pagesProb StatShinyDharNo ratings yet
- Constrained OptimizationDocument9 pagesConstrained OptimizationananyaajatasatruNo ratings yet
- Updated Directioal Derivatives and Gradients 4Document57 pagesUpdated Directioal Derivatives and Gradients 4Amna M . Nasr EldinNo ratings yet
- Chapter 2.4Document11 pagesChapter 2.4Foyshel RahmanNo ratings yet
- Chapter 2.4Document11 pagesChapter 2.4Atique FaisalNo ratings yet
- 1 Limits & Continuity NotesDocument82 pages1 Limits & Continuity Notesmseconroy84No ratings yet
- Random Variables and Probability DistributionDocument73 pagesRandom Variables and Probability Distributionkelihe8947No ratings yet
- OQM Lecture Note - Part 1 Introduction To Mathematical OptimisationDocument10 pagesOQM Lecture Note - Part 1 Introduction To Mathematical OptimisationdanNo ratings yet
- A Symmetric Function Approach To Polynomial Regression - Hans-Christian Herbig, Daniel Herden, Christopher SeatonDocument12 pagesA Symmetric Function Approach To Polynomial Regression - Hans-Christian Herbig, Daniel Herden, Christopher Seatonmohax74432No ratings yet
- For More Important Questions Visit:: Continuity and DifferentiationDocument8 pagesFor More Important Questions Visit:: Continuity and DifferentiationPrajith KanagarajNo ratings yet
- Lecture-1: Course Plan / OutlineDocument3 pagesLecture-1: Course Plan / OutlineNaiem IslamNo ratings yet
- Lec 04 - Week 04 Operations ResearchDocument56 pagesLec 04 - Week 04 Operations Researchbnzayd2005No ratings yet
- 1 Tan 6 6 Cos) Lim) Lim Cos) Lim 3 2 1 1 Sin (7) 3 3 5 1) Lim) Lim) Lim 4 2 10 6 10 2 1 1, 3 2 3 3) Lim ?) Lim 12 2, 3 3 2 1 1 Co) Lim) Lim 2 S SinDocument3 pages1 Tan 6 6 Cos) Lim) Lim Cos) Lim 3 2 1 1 Sin (7) 3 3 5 1) Lim) Lim) Lim 4 2 10 6 10 2 1 1, 3 2 3 3) Lim ?) Lim 12 2, 3 3 2 1 1 Co) Lim) Lim 2 S SinEng-Mukhtaar CatooshNo ratings yet
- Use of Mass Center To Prove InequalitiesDocument4 pagesUse of Mass Center To Prove InequalitiesResearch ParkNo ratings yet
- A Concept of Compromise Solution and The Method of The Displaced IdealDocument18 pagesA Concept of Compromise Solution and The Method of The Displaced IdealHeni AgustianiNo ratings yet
- Computer Aided Ship Design Part I. Optimization Method: Ch. 1 Overview of Optimal DesignDocument8 pagesComputer Aided Ship Design Part I. Optimization Method: Ch. 1 Overview of Optimal DesignSudarshan MadeswaranNo ratings yet
- Cal1 Econ Week2Document15 pagesCal1 Econ Week2Jaselle NamuagNo ratings yet
- Limit, Continuity and DifferentiabilityDocument64 pagesLimit, Continuity and DifferentiabilityVatsalyaNo ratings yet
- Grade (10) Chapter - 12 CalculusDocument33 pagesGrade (10) Chapter - 12 CalculusZakir Amad 32No ratings yet
- Opt Lecture 1Document13 pagesOpt Lecture 1hqfNo ratings yet
- Rules of Derivative PDFDocument28 pagesRules of Derivative PDFAriel Clopino PiolNo ratings yet
- Week 1Document17 pagesWeek 1Shavin ChandNo ratings yet
- Cal1 Econ Week1Document11 pagesCal1 Econ Week1ty laiNo ratings yet
- Debark University College of Natural and Computational Science Mathematics Department Applied Mathematics I YearDocument3 pagesDebark University College of Natural and Computational Science Mathematics Department Applied Mathematics I YearyacobNo ratings yet
- Assignment: Qualitative TheoryDocument70 pagesAssignment: Qualitative TheoryTahera ParvinNo ratings yet
- Lecture Note 1Document22 pagesLecture Note 1Pawan AichraNo ratings yet
- 05 1 Optimization Methods NDPDocument85 pages05 1 Optimization Methods NDPSebastian LorcaNo ratings yet
- UNIT-1 (Limits and Continuity)Document2 pagesUNIT-1 (Limits and Continuity)Dheeraj Krishna NeelamNo ratings yet
- NLP NctuDocument19 pagesNLP NctularasmoyoNo ratings yet
- Application of Derivatives: 6.1 Overview 6.1.1Document26 pagesApplication of Derivatives: 6.1 Overview 6.1.1Yashpal MishraNo ratings yet
- Chapter 3: The Lagrange Method: Elements of Decision: Lecture Notes of Intermediate MicroeconomicsDocument12 pagesChapter 3: The Lagrange Method: Elements of Decision: Lecture Notes of Intermediate MicroeconomicsAbdullahi ShehuNo ratings yet
- Lecture 9 - SVMDocument42 pagesLecture 9 - SVMHusein YusufNo ratings yet
- Linear Regression and Classification: Lectures 3-4Document41 pagesLinear Regression and Classification: Lectures 3-4ValNo ratings yet
- 1 References and ResourcesDocument6 pages1 References and ResourcesJerimiahNo ratings yet
- IEOR 160 Partial Lecture Notes 2017Document33 pagesIEOR 160 Partial Lecture Notes 2017Nate ArmstrongNo ratings yet
- Bio Stat 1Document19 pagesBio Stat 1Raj NagNo ratings yet
- Cooperating Intelligent Systems: Learning From Observations Chapter 18, AIMADocument51 pagesCooperating Intelligent Systems: Learning From Observations Chapter 18, AIMAapi-19643506No ratings yet
- ZimmermanDocument11 pagesZimmermanRavi VijNo ratings yet
- HW1 MLDocument2 pagesHW1 MLShashank SistlaNo ratings yet
- Genmath Module 2Document14 pagesGenmath Module 2Mori OugaiNo ratings yet
- Chapter 2B - Continuous: Random VariablesDocument20 pagesChapter 2B - Continuous: Random VariablesAhmad AiNo ratings yet
- Tutors: Prof. Dr. Tanka Nath Dhamala & Mr. Ram Chandra DhunganaDocument55 pagesTutors: Prof. Dr. Tanka Nath Dhamala & Mr. Ram Chandra DhunganaKapilNo ratings yet
- Tools 2022 05 26 22 32 24Document23 pagesTools 2022 05 26 22 32 24maxwell.karpzen99No ratings yet
- Image Filtering in Spatial DomainDocument36 pagesImage Filtering in Spatial DomainRafiq MuzakkiNo ratings yet
- HBR Marketing ManagementDocument67 pagesHBR Marketing ManagementSMNo ratings yet
- DerivativesDocument26 pagesDerivativesKavyaNo ratings yet
- Week 3 General MathematicsDocument10 pagesWeek 3 General MathematicsMarcel Baring ImperialNo ratings yet
- Hyperbolic FunctionsDocument9 pagesHyperbolic Functionstresa mariaNo ratings yet
- GLM Lec 1Document7 pagesGLM Lec 1HazemIbrahimNo ratings yet
- OPRE 6201: 4. Network Problems: 1.1 An LP FormulationDocument39 pagesOPRE 6201: 4. Network Problems: 1.1 An LP FormulationSajjad HossainNo ratings yet
- A Few More Past Exam Questions (Multiple Choice)Document6 pagesA Few More Past Exam Questions (Multiple Choice)exams_sbsNo ratings yet
- Optimization Problems: 1.1 Preliminary DefinitionsDocument4 pagesOptimization Problems: 1.1 Preliminary DefinitionsJǝ Ǝʌan M CNo ratings yet
- Nonlinear Functional Analysis and Applications: Proceedings of an Advanced Seminar Conducted by the Mathematics Research Center, the University of Wisconsin, Madison, October 12-14, 1970From EverandNonlinear Functional Analysis and Applications: Proceedings of an Advanced Seminar Conducted by the Mathematics Research Center, the University of Wisconsin, Madison, October 12-14, 1970Louis B. RallNo ratings yet
- I2204 Imperative Programming: DR Siba HaidarDocument7 pagesI2204 Imperative Programming: DR Siba HaidarAli MzayhemNo ratings yet
- Graph Theory: Lebanese University Faculty of Science BS Computer Science 2 Year - Fall SemesterDocument22 pagesGraph Theory: Lebanese University Faculty of Science BS Computer Science 2 Year - Fall SemesterAli MzayhemNo ratings yet
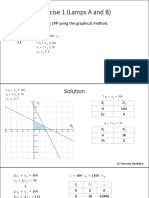
- Solve The Following LPP Using The Graphical Method. Maximize S.TDocument9 pagesSolve The Following LPP Using The Graphical Method. Maximize S.TAli MzayhemNo ratings yet
- Matrix Form of LPP: Maximize S.T. WhereDocument14 pagesMatrix Form of LPP: Maximize S.T. WhereAli MzayhemNo ratings yet
- Graph Theory: Lebanese University Faculty of Science BS Computer Science 2 Year - Fall SemesterDocument77 pagesGraph Theory: Lebanese University Faculty of Science BS Computer Science 2 Year - Fall SemesterAli MzayhemNo ratings yet
- Info 2201 Client-Side Web Development: Lebanese University Faculty of Sciences - Section I BS-Computer ScienceDocument39 pagesInfo 2201 Client-Side Web Development: Lebanese University Faculty of Sciences - Section I BS-Computer ScienceAli MzayhemNo ratings yet
- Lebanese University Faculty of Science BS Computer Science 2 Year - Fall SemesterDocument21 pagesLebanese University Faculty of Science BS Computer Science 2 Year - Fall SemesterAli MzayhemNo ratings yet
- Graph Theory: Lebanese University Faculty of Science BS Computer Science 2 Year - Fall SemesterDocument78 pagesGraph Theory: Lebanese University Faculty of Science BS Computer Science 2 Year - Fall SemesterAli MzayhemNo ratings yet
- I2201 Chapter 6 TablesDocument24 pagesI2201 Chapter 6 TablesAli Mzayhem0% (1)
- Info 2201 Client-Side Web Development: Lebanese University Faculty of Sciences - Section I BS-Computer ScienceDocument36 pagesInfo 2201 Client-Side Web Development: Lebanese University Faculty of Sciences - Section I BS-Computer ScienceAli MzayhemNo ratings yet
- Info 2201 Client-Side Web Development: Lebanese University Faculty of Sciences - Section I BS-Computer ScienceDocument23 pagesInfo 2201 Client-Side Web Development: Lebanese University Faculty of Sciences - Section I BS-Computer ScienceAli MzayhemNo ratings yet
- Chap 2Document47 pagesChap 2Ali MzayhemNo ratings yet
- I2201 - Chapter 4 - Visula Elements, Graphics and Web MultimediaDocument46 pagesI2201 - Chapter 4 - Visula Elements, Graphics and Web MultimediaAli MzayhemNo ratings yet
- Chap 3Document34 pagesChap 3Ali MzayhemNo ratings yet
- 1.draw The Circuit Diagram of A Mod-16 Asynchronous Counter and Explain Its Working WithDocument4 pages1.draw The Circuit Diagram of A Mod-16 Asynchronous Counter and Explain Its Working WithRajeshwari SNo ratings yet
- Improved Mini-Silo For Studying Fermentation of Silage in Laboratory ConditionsDocument8 pagesImproved Mini-Silo For Studying Fermentation of Silage in Laboratory ConditionsCk_psihNo ratings yet
- Depot 69.F1D6B066Document164 pagesDepot 69.F1D6B066CĐXN5B 19— Lê Hữu MinhNo ratings yet
- Incubator GinevriDocument24 pagesIncubator GinevriDivino Elisanto SitinjakNo ratings yet
- Rocket PropulsionDocument29 pagesRocket PropulsionPrajwal Vemala JagadeeshwaraNo ratings yet
- Noise PollutionDocument17 pagesNoise Pollutionmelannie adanteNo ratings yet
- 6553 Unit No 1 EmaadDocument26 pages6553 Unit No 1 Emaaduzma gulNo ratings yet
- Tracing The Location of A Typhon Lesson PlanDocument4 pagesTracing The Location of A Typhon Lesson PlanJoh A Nna100% (2)
- Be11 enDocument12 pagesBe11 enSaqlain Mir100% (1)
- PHY11L E201: Work, Energy, and PowerDocument16 pagesPHY11L E201: Work, Energy, and PowerMikaella TambisNo ratings yet
- Kirlian PhotographyDocument18 pagesKirlian PhotographyjoseNo ratings yet
- Chapter 1 (Marketing Updated)Document9 pagesChapter 1 (Marketing Updated)i211416 Shizza KianiNo ratings yet
- Unit1 Topic1 Digital Logic IntroductionDocument33 pagesUnit1 Topic1 Digital Logic IntroductionHari Kumar N CNo ratings yet
- Curva Desempeño - Folleto - Power Flo - IIDocument2 pagesCurva Desempeño - Folleto - Power Flo - IIHenry MartinezNo ratings yet
- 2.5 Insulation & RefractoriesDocument9 pages2.5 Insulation & Refractoriesriyazcomm_257961932No ratings yet
- Demographics Data Table: Lesson 1: Step 1Document3 pagesDemographics Data Table: Lesson 1: Step 1Julia AbreuNo ratings yet
- TI C5510 Assembly ProgrammingDocument21 pagesTI C5510 Assembly ProgrammingWinsweptNo ratings yet
- Chapter 5.0.2018 - Retaining WallDocument36 pagesChapter 5.0.2018 - Retaining WallHawaiiChongNo ratings yet
- 21st Bomber Command Tactical Mission Report 64, 65, OcrDocument57 pages21st Bomber Command Tactical Mission Report 64, 65, OcrJapanAirRaidsNo ratings yet
- A Report: Smt. Shantaben Haribhai Gajera Engineering CollegeDocument5 pagesA Report: Smt. Shantaben Haribhai Gajera Engineering CollegePranav. ThubeNo ratings yet
- Q4 TLE AFA Horticulture 9 Week3Document4 pagesQ4 TLE AFA Horticulture 9 Week3Dash Bello100% (1)
- 05-Chapter 2Document29 pages05-Chapter 2Atul RanjanNo ratings yet
- JLG 860SJ Parts - Global - English PDFDocument294 pagesJLG 860SJ Parts - Global - English PDFfater esmandarNo ratings yet
- Sec D CH 12 Regression Part 2Document66 pagesSec D CH 12 Regression Part 2Ranga SriNo ratings yet
- CH 15Document42 pagesCH 15mah b0% (1)
- 03 QPythons Main FeaturesDocument4 pages03 QPythons Main FeaturesJack Ahm PeaceNo ratings yet
- HS527 SilvanChipDocument3 pagesHS527 SilvanChipBouhafs AbdelkaderNo ratings yet
- Social Construction of DisasterDocument385 pagesSocial Construction of DisasterPratik Kumar BandyopadhyayNo ratings yet
- Summit 1 HomeworkDocument6 pagesSummit 1 HomeworkMaycol Antonio RojasNo ratings yet
- TKL Pump - Data - SheetDocument1 pageTKL Pump - Data - Sheetธนาชัย เต็งจิรธนาภาNo ratings yet