PRESSURE DRAWDOWN TEST ANALYSES

Pressure drawdown tests can be conducted any time in the life of the well, but usually and in
most common field practices they are run after a buildup test when the reservoir pressure is
uniform, i.e., stabilized.

CONSTANTRATE PRESSURE DRAWDOWN TEST

To conduct a constant-rate pressure drawdown test the well is produced at constant rate and
the bottomhole flowing pressure p wf is simultaneously recorded with time.

Recall that the drawdown equation is the infinite acting solution of the diffusivity equation.
It is given as:

   
162 .6 qB    k 
p wf  p i  log( t )  log  3.23  0.869 s  (1)
  2  
  ct rw 
kh
 

or
   
p wf  p i  m log( t )  log    3.23  0.869 s 
k
(2)
  2 
   ct rw  

where:
162 .6 qB 
m (3)
kh

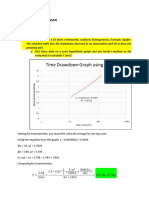
A plot of p wf vs. t on semilog graph paper should yield a straight-line with slope m after
the cessation of the wellbore storage. The end of wellbore storage is determined in the same
manner as in pressure buildup analysis. The only difference is that the X-axis of the log-log
plot consists of t and the Y-axis consists of  p  p i  p wf .

p wf

log(t )
Typical constant-rate drawdown test graph

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 1

Methodology
1. Plot p wf vs. t on semilog graph paper.

2. Determine the end of wellbore storage (wellbore unloading), i.e., beginning of the
middle-time region (MTR). If not properly detected, wellbore storage can cause many
problems in well test analysis.
Few of these problems are:
a. Delay in the beginning of the MTR, making its recognition more difficult.
b. Total lack of development of the MTR in some cases, with relatively long periods of
afterflow and relatively early onset of boundary effects.
c. Development of several false straight-lines, any of which could be mistaken for the
MTR line.
Three methods are used to estimate the end of wellbore storage effects:
Method 1
i Calculate  p  p i  p wf , p i is the pressure at t  0 , i.e., the beginning of the test.

ii. Plot  p vs. t on log-log graph paper.

iii. Draw the unit-slope line (45 line).

iv. Wellbore storage distortion ends about 1½cycle in time after the log-log data plot
starts deviating from the unit-slope line.
Method 2
i. Calculate the derivative of flowing BHP ( p wf ) with respect to time, t ,
'  d( p
p wf wf / dt ) , or pressure drop derivative with respect to time,
'  d ( p
p wf wf / dt ) .

' vs. t or
ii. Multiply the pressure derivative calculated in step (i) by t and plot  t p wf
' vs. t on the same graph of  p
 t p wf wf vs. t .

iii. Wellbore storage effects end when the pressure derivative plot flattens out (it becomes
more or less horizontal).

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 2

 1000

100

pwf, psi

-t p'wf 10
or
-t p'wf

0.1
0.00001 0.0001 0.001 0.01 0.1 1 10 100
t, hr

Method 3
Match the log-log plot with Ramey’s type curve Fig. 4.1 p. 64, i.e., to make an
appropriate match the log-log plot should have the same grids as Ramey’s curve. When
the replotted curve for finite value of C D becomes identical to the curve for C D  0 ,
this point on the actual data is the end of wellbore storage distortion.
To make the match easier do the following:
i. Calculate the wellbore storage coefficient C as:
25.65 Awb
C , bbl/psi (4)


or
qB t
C , bbl/psi (5)
24 p

t and  p are the coordinates of any point on the unit-slope line.

ii. Calculate the dimensionless wellbore storage coefficient C D as:

0.894C
CD  (6)
 ct hrw2

C D gives the range where the match should be attempted.

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 3

 Notes:
i. Even though the semi-log graph is more sensitive to pressure changes and it gives a
good estimate of the beginning of the straight-line, it is important to verify this
estimate by the pressure derivative plot and the log-log curve matching.
ii. Of course the boundary effects appear when the data start to deviate from the semi-log
straight-line at the end of MTR. The time for boundary effects (late time region, LTR)
can be estimated from the semi-log plot and verified using the pressure derivative and
the log-log plots.
3. Determine the slope m of the straight-line portion of the curve.
4. Calculate the formation permeability k from the slope as:
162.6 qB
k , md (7)
mh

5. Calculate the skin factor s using the following equation:

p  p   
s  1.151 i 1hr  log  k   3.23 (8)
  2  
  ct rw 
m
 

p1hr is obtained from the straight-line portion of the curve or its extrapolation for
t  1 hr .

6. Calculate the pressure drop due to skin p s as:

141.2 qB
p s  s  0.869 ms , psi (9)
kh

p s indicates the effect of damage or stimulation on well performance, i.e., production

rate in terms of pressure drop. A positive p s means that part of the driving energy is
lost in the damaged zone. If the damage is removed the well can produce more oil or
produce at the same rate with less pressure drop.

7. Calculate the effective wellbore radius rwa as:

rwa  rw e  s , ft. (10)

rwa  rw indicates a damaged well.

rwa  rw indicates a stimulated well.

8. Calculate the flow efficiency E as:

J actual
E
J ideal

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 4

 pi  p wf  p s p s
E  1 (11)
pi  p wf pi  p wf

E  1 for stimulated wells.

E  1 for damaged wells.

E can be determined at any time during the test; in this case p i = pressure at t  0 and
p wf = pressure at time t .

A stimulated well with a flow efficiency of two produces twice as much fluid with a
given pressure drawdown as it would have if it was not stimulated.
A damaged well with a flow efficiency of 0.1 produces 10% as much fluid with a given
pressure drawdown as it would have if the damage were removed.

9. Calculate the damage ratio 1 / E as:

1 pi  p wf
 (12)
E pi  p wf  p s

10. Calculate the damage factor = 1  E

11. Calculate the radius of investigation ri as:

kt
ri  , ft. (13)
948  ct

ri indicates the influence of production in terms of distance from the wellbore, i.e., the
distance a significant pressure disturbance is propagated by production or injection at
constant rate. It reflects the portion or region of the reservoir sampled during the MTR.
That region is given by ri achieved by the production or injection transient at the start
and end of the MTR. This is very important because the distance a transient has moved
into the formation is approximately the distance from the well at which formation
properties are being investigated at a particular time in a well test. The larger the
distance is, the better and more significant the results of the well tests are.
Furthermore, the radius of investigation concept provides a guide for well test design.
For example, we may want to sample reservoir properties at least 500 ft from the well.
How long a test shall be run? 6 hrs? 20 hrs? We are not forced to guess or to run a test
for an arbitrary length of time that could be either too short or too long. Instead, we can
use the radius of investigation equation to estimate the time required to test to the desired
depth in the formation.

12. Calculate the permeability of the altered zone k s as:

k
ks  , md (14)
s
r 
ln  s  1

 rw 

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 5

13. Calculate the wellbore storage coefficient C using Eq. 4 or 5 as:

A
C  25 .65 wb , bbl/psi (4)


qB t
C , bbl/psi (5)
24 p

14. Calculate the wellbore storage duration t wbs as:

( 200,000  12,000 s ) C
t wbs  , hr (15)
kh / 

match t wbs with that obtained from the log-log plot.

RESERVOIR LIMIT TEST

A reservoir limit test is a drawdown test that is specifically run to estimate the reservoir
volume communicating with the well. The well is put on production long enough so that the
effect of production ( ri ) reaches all reservoir boundaries (PSS).

Recall the PSS solution of the diffusivity equation:

141.2 qB  0.000527 kt r  3 

p wf  pi    ln  e    s  (16)
kh   c r 2  rw  4 
 t e 

differentiating Eq. 16 with respect to time we obtain:

 p wf 0 .0744 qB
 (17)
t  ct h re2

The liquid-filled pore volume is given as:

V p   re2 h (18)

substituting Eq. 18 into Eq. 17 we obtain:

 p wf 0.234 qB
 (19)
t ct V p

A plot of p wf vs. t on Cartesian graph paper should yield a straight-line with slope m *
defined as:
0.234 qB
m*   , psi/hr (20)
ct V p

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 6

Methodology

1. plot p wf vs. t on Cartesian graph paper.

2. Determine the slope m * of the straight-line.

3. Calculate the area drained by the well as:
0.234 qB
A , ft.2 (21)
 ct h m *

or in acres, the area is given as:

0.234 qB
A , acre (22)
43560  ct h m *

4. Calculate the connected reservoir-drainage volume as:

0.234 qB
V p   hA  , ft 3 (23)
ct m *

or in bbl, the reservoir drainage-volume is given as:

 hA 0.234 qB
Vp   , res. bbl (24)
5.615 5.615 ct m *

or:
q
Vp  , STB (24a)
24 ct m *

V p is also the oil-in-place with S o  100% .

5. Calculate the shape factor of the reservoir C A as:

5.456 m  2.303 ( p1hr  pint ) 

CA  Exp   (25)
m*  m 

where:
m and p1hr are obtained from the semilog plot during the infinite acting period. m * and
pint are obtained from the Cartesian plot during the PSS period.
Note: maintain the signs of m and m *

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 7

Knowing the shape factor, use Table 1.2 p. 9-10 (Handout Table D-1 p. 265-266) to
determine the reservoir configuration with the shape factor closest to that calculated from Eq.
25 or calculate:

0.1833 m * 0.0002637 k
(t DA ) pss  t pss  t pss (26)
m  ct A

t pss is obtained from the Cartesian plot, i.e., beginning of the straight-line portion of the
curve. Having (t DA ) pss use “exact for t DA  ” column of Table 1.2 p. 9-10 (Handout
Table D-1 p. 265-266) to determine the reservoir configuration.

TWORATE FLOW TEST

In this test the well is produced at constant rate q1 for time t1 before the production rate is
changed to another constant rate q 2 where the well is produced for time  t as shown in the
figure below.

q1

q q2

t

t1

time
Rate history for two-rate flow test
Rate schedule history for two-rate flow test

Applying superposition to the infinite acting solution of the diffusivity equation we obtain:
   
162 .6 q 2 B 
p wf  p i   log  k   3.23  0.869 s 
kh    c r 2  
  t w 

162 .6 q1 B   t1  t  q 2 
 log   log( t )  (27)
kh   t  q1 

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 8

Eq. 27 can be written as:

   
162 .6 q 2 B    3.23  0.869 s   m log  t1   t   
log  k q2
p wf  p i   log(  t ) 
kh    c r 2     t  q1 
  t w 
(28)
where:
q1 : first flow rate, i.e., rate prior to rate change.
q2 : second flow rate, i.e., rate after the rate change.
t1 : producing time prior to rate change.
t : producing time measured from the instant of rate change.
and m is defined as:

162.6 q1B
m (29)
kh

  t  t  q 2 
A plot of p wf vs. log  1  log( t )  on Cartesian graph paper should yield a
  t  q1 
straight-line with slope m .

Methodology

  t  t  q 2 
1. Calculate log  1  log( t )  .
  t  q1 
  t  t  q 2 
2. Plot the pressure after the rate change p wf vs. log  1  log( t )  on Cartesian
  t  q1 
graph paper.
3. Determine the slope of the straight-line portion of the curve.
4. Calculate the formation permeability k as:

162.6 q1B
k , md (30)
mh
5. Calculate the skin factor s as:

  p1hr  p wf    
s  1.151
q1
    log  k   3.23 (31)
 q1  q 2    2  
  m    ct rw  

where:
p wf : pressure at the time of rate change, i.e., t  0.
p1hr : pressure at 1 hr after the rate change on the straight-line portion of the flow
test curve.

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 9

6. Calculate p i or p * as:

   
p i  p wf 1  m log    3.23  0.869 s  , psi
k t1
(32)
   c r 2  
  t w  
where:
p wf 1 : the pressure at the beginning of the second flow rate, psi
t1 : time at the beginning of the second flow rate, hr

VARIABLE RATE TESTS

WINESTOCK AND COLPITTS TECHNIQUE

Schematic illustration of the variable sandface flow rate test

Schematic illustration of the variable sandface flow rate

Winestock and Colpitts equation is given as:

p i  p wf    
162 .6 B   log( t )  log  k   3.23  0.869 s 
 (33)
  2 
  ct rw 
q (t ) kh
 
Eq. 33 can be written as:

p i  p wf    
 m ' log( t )  log    3.23  0.869 s 
k
(34)
  2 
  ct rw 
q (t )
 
where:
162 .6 B
m'  (35)
kh
p i  p wf
A plot of vs. t on semilog graph should yield a straight-line with slope m ' .
q (t )

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 10

Methodology

p i  p wf
1. Calculate
q (t )

p i  p wf
2. Plot vs. t on semilog graph paper.
q (t )
3. Determine the slope m ' of the straight-line portion of the curve.
4. Calculate the formation permeability k as:
162 .6 B 
k , md (36)
m' h

5. Calculate the skin factor s as:

 p p    
1
s  1.151 
i wf   log  k   3.23 (37)

 m'    2  
  ct rw 
q (t ) 1hr
 

where:

 pi  p wf 
  is obtained from the straight-line portion of the curve or its extrapolation
 q (t ) 1hr
for t  1 hr.

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 11

6. Calculate the wellbore storage coefficient C using either Eqs. 4 or 5 as:

Awb
C  25 .65 , bbl/psi (4)


qB t
C , bbl/psi (5)
24 p

7. Calculate the end of wellbore storage time t wbs as:

( 200,000  12,000 s ) C
t wbs  , hr (38)
kh / 

check if t wbs calculated using Eq. 37 match the one picked on the straight-line.

MULTIPLE-RATE TEST

Rate history for multirate test

Applying superposition to the infinite acting solution of the diffusivity equation we obtain:

pi  p wf n q q    
j 1
log( t n  t j 1 )  m ' log   3.23  0.869 s 
j k
qn
 m'  qn    c r 2  
j 1   t w 
(39)

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 12

 p i  p wf n q q
j j 1
A plot of vs.  log( t n  t j 1 ) on Cartesian graph paper should yield
qn qn
j 1
a straight-line with slope m ' and intercept b ' where:
162 .6 B 
m'  (40)
kh

   
b '  m ' log    3.23  0.869 s 
k
(41)
   c r 2  
  t w 

Note: It is important to understand that the rate corresponding to each plotted pressure point
is q n , i.e., the last rate that can affect that pressure.

Methodology

pi  p wf n q q
j j 1
1. Calculate and  log( t n  t j 1 )
qn qn
j 1

pi  p wf n q q
j j 1
2. Plot
qn
 q
vs. log( t n  t j 1 ) on Cartesian graph paper.
j 1 n
3. Determine the slope of the straight-line m ' and the intercept b ' .
4. Calculate the formation permeability k as:
162.6 B
k , md (42)
m' h

5. Calculate the skin factor s as:

   
s  1.151 b'
 log  k   3.23 (43)
 m'  2  
   ct rw  

Module 8 – Pressure Drawdown Tests Prof. Ibrahim Sami Nashawi 13