Fundamentals of Electric Circuits, Second Edition - Alexander/Sadiku 1

Chapter 14, Problem 6(6).

Obtain the transfer function H(ω) = Io/Is of the circuits shown in Fig. 14.70.

Figure 14.70

Chapter 14, Solution 6(6).

Using current division,

Io R
H (ω) = =
I i R + jωL + 1 jωC

jωRC jω (20)(0.25)
H (ω) = =
1 + jωRC − ω LC 1 + jω(20)(0.25) − ω2 (10)(0.25)
2

jω5
H (ω) =
1 + jω5 − 2.5 ω 2

Copyright ©2004 The McGraw-Hill Companies Inc.

Fundamentals of Electric Circuits, Second Edition - Alexander/Sadiku 2

We apply nodal analysis to the circuit below.

0.5 Vx
Io 1/jwC
Vx
+ -

Is R jwL

Vx Vx − 0.5Vx
Is = +
R jωL + 1 jωC

0.5 Vx
But Io = 
→ Vx = 2 I o ( jωL + 1 jωC)
jωL + 1 jωC

Is 1 0 .5
= +
Vx R jωL + 1 jωC

Is 1 1
= +
2 I o ( jωL + 1 jωC) R 2 ( jωL + 1 jωC)

I s 2 ( jωL + 1 jωC)
= +1
Io R

Io 1 jωRC
H (ω) = = =
I s 1 + 2 ( jωL + 1 jωC) R jωRC + 2 (1 − ω 2 LC)
jω
H (ω) =
jω + 2 (1 − ω2 0.25)

jω
H (ω) =
2 + jω − 0.5 ω 2

Copyright ©2004 The McGraw-Hill Companies Inc.

 Fundamentals of Electric Circuits, Second Edition - Alexander/Sadiku 1

Chapter 14, Problem 29.

For the circuit in Fig. 14.74, find the frequency ω for which v(t) and i(t) are in
phase.

Figure 14.74

Chapter 14, Solution 29.

jω 1/jω

Z
1 jω

1 jω
Z = jω + +
j ω 1 + jω

 1  ω 2 + jω
Z = j ω −  +
 ω  1 + ω2

Since v( t ) and i( t ) are in phase,

1 ω
Im(Z) = 0 = ω − +
ω 1 + ω2

ω4 + ω2 − 1 = 0

-1 ± 1+ 4
ω2 = = 0.618
2

ω = 0.7861 rad / s

Copyright ©2004 The McGraw-Hill Companies Inc.

 Fundamentals of Electric Circuits, Second Edition - Alexander/Sadiku 1

Chapter 14, Problem 40.

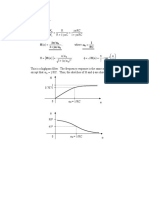
For the circuit shown in Fig. 14.77: (a) Calculate the resonant frequency ωo, the
quality factor Q, and the bandwidth B. (b) What value of capacitance must be
connected in series with the 20-µF capacitor in order to double the bandwidth?

Figure 14.77
(b)
(c)
Chapter 14, Solution 40.

(a) L = 5 + 10 = 15 mH

1 1
ω0 = = = 1.8257 k rad/sec
LC −3 −6
15x10 x 20x10

Q = ω0 RC = 1.8257 x10 3 x 25x10 3 x 20x10 −6 = 912.8

1 1
B= = = 2 rad
RC 25x10 3 20x10 −6

(b) To increase B by 100% means that B’ = 4.

1 1
C′ = = = 10 µF
RB′ 25x10 3 x 4

C1C 2
Since C′ = = 10µF and C1 = 20 µF, we then obtain C2 = 20 µF.
C1 + C 2

Therefore, to increase the bandwidth, we merely add another 20 µF in

series with the first one.

Copyright ©2004 The McGraw-Hill Companies Inc.

 Fundamentals of Electric Circuits, Second Edition - Alexander/Sadiku 1

Chapter 14, Problem 42.

Calculate the resonant frequency of each of the circuits in Fig. 14.79.

Figure 14.79

Chapter 14, Solution 42.

Z in = (1 jωC) || (R + jωL)

R + jωL
jωC R + jωL
Z in = =
1 1 − ω2 LC + jωRC
R + jωL +
jωC

(R + jωL)(1 − ω2 LC − jωRC)
Z in =
(1 − ω2 LC) 2 + ω2 R 2 C 2

At resonance, Im(Z in ) = 0 , i.e.

0 = ωL(1 − ω2 LC) − ωR 2 C
ω2 LC = L − R 2 C

L − R 2C 1 R2
ω0 = = −
LC C L

Copyright ©2004 The McGraw-Hill Companies Inc.

 Fundamentals of Electric Circuits, Second Edition - Alexander/Sadiku 1

Chapter 14, Problem 45.

For the network illustrated in Fig. 14.82, find

(a) the transfer function H(ω) = Vo(ω)/I(ω),

(b) the magnitude of H at ω0 = 1 rad/s.

Figure 14.82
(b)
(c)
Chapter 14, Solution 45.

jω 1 1 jω 1
1 || jω = , 1 || = =
1 + jω jω 1 + 1 jω 1 + jω

Transform the current source gives the circuit below.

jω 1 +
jω + 1
I 1 + jω Vo
1 + jω - 1 + jω
-

1
1 + jω jω
Vo = ⋅ I
1 jω 1 + j ω
1+ +
1 + jω 1 + jω

Vo jω
H (ω) = =
I 2 (1 + jω) 2

1 1
H (1) = H (1) = = 0.25
2 (1 + j) 2 2 ( 2)2

Copyright ©2004 The McGraw-Hill Companies Inc.