Professional Documents
Culture Documents
General Leibniz Rule - Wikipedia
Uploaded by
Arshad KhanOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
General Leibniz Rule - Wikipedia
Uploaded by
Arshad KhanCopyright:
Available Formats
Search Wikipedia
General Leibniz rule
… … …
For other uses, seeLeibniz's rule (disambiguation)
.
In calculus, the general Leibniz rule,[1] named after Gottfried Wilhelm Leibniz, generalizes the
product rule (which is also known as "Leibniz's rule"). It states that if and are -times
differentiable functions, then the product is also -times differentiable and its th derivative is
given by
where is the binomial coefficient and denotes the jth derivative of f (and
in particular ).
The rule can be proved by using the product rule and mathematical induction.
Contents
Second derivative …
If, for example, n = 2, the rule gives an expression for the second derivative of a product of two
functions:
More than two factors …
The formula can be generalized to the product of m differentiable functions f1,...,fm.
where the sum extends over all m-tuples (k1,...,km) of non-negative integers with and
are the multinomial coefficients. This is akin to the multinomial formula from algebra.
Proof …
The proof of the general Leibniz rule proceeds by induction. Let and be -times differentiable
functions. The base case when claims that:
which is the usual product rule and is known to be true. Next, assume that the statement holds for
a fixed that is, that
Then,
And so the statement holds for and the proof is complete.
Multivariable calculus …
With the multi-index notation for partial derivatives of functions of several variables, the Leibniz
rule states more generally:
This formula can be used to derive a formula that computes the symbol of the composition of
differential operators. In fact, let P and Q be differential operators (with coefficients that are
differentiable sufficiently many times) and Since R is also a differential operator, the
symbol of R is given by:
A direct computation now gives:
This formula is usually known as the Leibniz formula. It is used to define the composition in the
space of symbols, thereby inducing the ring structure.
See also …
Binomial theorem
Derivation (differential algebra)
Derivative
Differential algebra
Pascal's triangle
References …
1. ^ Olver, Peter J. (2000). Applications of Lie Groups to Differential Equations . Springer. pp. 318–319.
Last edited 9 months ago by Chongkian
RELATED ARTICLES
Differential
Multi-index Pseudo-
algebra
notation differential
Algebra with a formal…
operator
Content is available under CC BY-SA 3.0 unless otherwise noted.
Terms of Use • Privacy policy • Desktop
You might also like
- Art of Problem SolvingDocument3 pagesArt of Problem SolvingeleslusNo ratings yet
- The Differential CalculusDocument42 pagesThe Differential CalculusAbdul Halil AbdullahNo ratings yet
- MooculusDocument267 pagesMooculusCrizelle Joy ArceNo ratings yet
- I. Real NumbersDocument11 pagesI. Real NumbersClarin James Ryan P.No ratings yet
- First-Order Modal LogicDocument15 pagesFirst-Order Modal LogicFrank Campos100% (1)
- Calculus 1Document230 pagesCalculus 1Abdul Halil Abdullah100% (1)
- Lavau-Palmkvist2020 Article Infinity-enhancingOfLeibnizAlgDocument32 pagesLavau-Palmkvist2020 Article Infinity-enhancingOfLeibnizAlgKaliNo ratings yet
- Lesson 7 Composite and Implicit Functions For Two Variables: Module 1: Differential CalculusDocument9 pagesLesson 7 Composite and Implicit Functions For Two Variables: Module 1: Differential CalculussubhradeepNo ratings yet
- Name of Learner: - SectionDocument4 pagesName of Learner: - SectionJay Jexter SeldaNo ratings yet
- On Fibonacci Functions With Fibonacci NumbersDocument8 pagesOn Fibonacci Functions With Fibonacci NumbersSANIKA VERMANo ratings yet
- Leibniz Integral Rule - WikipediaDocument70 pagesLeibniz Integral Rule - WikipediaMannu Bhattacharya100% (1)
- The Calculi of Lambda-Conversion (AM-6), Volume 6From EverandThe Calculi of Lambda-Conversion (AM-6), Volume 6Rating: 4 out of 5 stars4/5 (1)
- Introduction To The Theory of Fuzzy SubsetsDocument1 pageIntroduction To The Theory of Fuzzy SubsetsSangeethaNo ratings yet
- Multivariable CalculusDocument5 pagesMultivariable CalculusNirmal BhowmickNo ratings yet
- What Is A Partial Differential Equation?Document24 pagesWhat Is A Partial Differential Equation?Cayuss Andrei MihăițoaiaNo ratings yet
- Lecture Note On Mathematical Methods I MDocument66 pagesLecture Note On Mathematical Methods I MAyomikunNo ratings yet
- Module 2, Lsseon 3Document8 pagesModule 2, Lsseon 3alayca cabatanaNo ratings yet
- Calculus 1 Lessons on Differentiation Rules, Rates of Change, Trig Functions and MoreDocument217 pagesCalculus 1 Lessons on Differentiation Rules, Rates of Change, Trig Functions and MoreAbdul Halil Abdullah0% (1)
- Lagrangian Mechanics 4Document13 pagesLagrangian Mechanics 4Sahibnoor SinghNo ratings yet
- Ilang - Ilang LP g7Document6 pagesIlang - Ilang LP g7custodiokeizelNo ratings yet
- Studentchap8 2017Document5 pagesStudentchap8 2017lxluthr0No ratings yet
- The Neumann Problem for the Cauchy-Riemann Complex. (AM-75), Volume 75From EverandThe Neumann Problem for the Cauchy-Riemann Complex. (AM-75), Volume 75Rating: 4 out of 5 stars4/5 (2)
- Numerical Analysis TechniquesDocument122 pagesNumerical Analysis TechniquesThotakuri Sai Amith ChowdaryNo ratings yet
- Picard-Lindelöf Theorem - Wikipedia, The Free EncyclopediaDocument4 pagesPicard-Lindelöf Theorem - Wikipedia, The Free EncyclopediaMala MessierNo ratings yet
- Integral - From Wolfram MathWorldDocument1 pageIntegral - From Wolfram MathWorldE.No ratings yet
- Pptca1 13030823093 BSM101 Aiml BDocument8 pagesPptca1 13030823093 BSM101 Aiml BAJIT PRASAD 12- C. Roll-04No ratings yet
- Fundamental Theorem of Calculus Definition and ApplicationsDocument11 pagesFundamental Theorem of Calculus Definition and ApplicationsaaaahsanNo ratings yet
- Legendre TransformDocument6 pagesLegendre TransformGunnar CalvertNo ratings yet
- Learning Objectives: Guide No. 4: Boolean AlgebraDocument6 pagesLearning Objectives: Guide No. 4: Boolean AlgebraJavi CuervoNo ratings yet
- 2.1 Derivatives of Algebraic and Transcendental FunctionsDocument15 pages2.1 Derivatives of Algebraic and Transcendental FunctionsFabie BarcenalNo ratings yet
- Chapter 3 NotesDocument34 pagesChapter 3 NotesNoreen YinNo ratings yet
- Differentiation Rules: CalculusDocument7 pagesDifferentiation Rules: CalculusRahul ShankhwarNo ratings yet
- Operational FunctionsDocument8 pagesOperational FunctionsArmySapphireNo ratings yet
- LAnotesDocument51 pagesLAnotesslurm101No ratings yet
- (2019) - Shirali Satish & Vasudeva Lal. Measure and IntegrationDocument609 pages(2019) - Shirali Satish & Vasudeva Lal. Measure and IntegrationJorge JGNo ratings yet
- Math 1102 (Ch-4) - Applied Mathematics II-1Document25 pagesMath 1102 (Ch-4) - Applied Mathematics II-1IbsaNo ratings yet
- List of IntegralsDocument10 pagesList of IntegralsRahul ShankhwarNo ratings yet
- 4Chapter12 P1 Boolean Algebra Boolean FunctionsDocument18 pages4Chapter12 P1 Boolean Algebra Boolean Functionsknbx7xcm9cNo ratings yet
- Calculus of Several Variable FunctionsDocument61 pagesCalculus of Several Variable FunctionsShashikala RajuNo ratings yet
- Data Structure Part 1 50 MCQ CexamindiaDocument21 pagesData Structure Part 1 50 MCQ Cexamindiashristy kumariNo ratings yet
- Function Theoretic Methods in Partial Differential EquationsFrom EverandFunction Theoretic Methods in Partial Differential EquationsNo ratings yet
- AI Module4Document33 pagesAI Module4onionb443No ratings yet
- Complex Eigenvalues Best++++Document16 pagesComplex Eigenvalues Best++++lostkinNo ratings yet
- PreCalculus Fall 2012 Lesson 018 - Inverse FunctionsDocument4 pagesPreCalculus Fall 2012 Lesson 018 - Inverse FunctionsEel DemlaNo ratings yet
- Lesson Plan On AlgebraDocument5 pagesLesson Plan On AlgebrasairajNo ratings yet
- Term Paper of Mathematics On Ordinary Differential Equations of Higher OrderDocument4 pagesTerm Paper of Mathematics On Ordinary Differential Equations of Higher OrderSagnik DasNo ratings yet
- Leibniz integral rule - WikipediaDocument16 pagesLeibniz integral rule - Wikipediadarnit2703No ratings yet
- Multivariable Calculus: 1 Typical OperationsDocument3 pagesMultivariable Calculus: 1 Typical Operationsanon_482623913100% (1)
- MSc Analysis I DifferentiationDocument92 pagesMSc Analysis I Differentiationakangsa lodhNo ratings yet
- Corepure2 Chapter 6::: Hyperbolic FunctionsDocument46 pagesCorepure2 Chapter 6::: Hyperbolic FunctionsMadalina ChiriloiNo ratings yet
- Wikibooks Accepts Video Game Strategy GuidesDocument125 pagesWikibooks Accepts Video Game Strategy GuidesVernon MonteiroNo ratings yet
- Cu 31924031254042Document180 pagesCu 31924031254042Paul TurnerNo ratings yet
- DLL GenMath LogarithmicDocument3 pagesDLL GenMath LogarithmicNicole MoscaNo ratings yet
- Antiderivatives and Indefinite Integrals: Integral CalculusDocument8 pagesAntiderivatives and Indefinite Integrals: Integral CalculusZak KeroumNo ratings yet
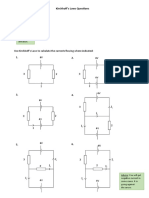
- 09 Kirchhoff's Laws QuestionsDocument1 page09 Kirchhoff's Laws QuestionsArshad KhanNo ratings yet
- 6.1 - Aromatic Compounds, Carbonyls and AcidsDocument28 pages6.1 - Aromatic Compounds, Carbonyls and AcidsArshad KhanNo ratings yet
- 5.1 - Rates, Equilibrium and PH: 5.1.1 - How Fast?Document26 pages5.1 - Rates, Equilibrium and PH: 5.1.1 - How Fast?Arshad KhanNo ratings yet
- FlashcardsDocument4 pagesFlashcardsArshad KhanNo ratings yet
- The periodic table and qualitative analysisDocument13 pagesThe periodic table and qualitative analysisArshad KhanNo ratings yet
- Thermal Physics FlashcardsDocument8 pagesThermal Physics FlashcardsArshad KhanNo ratings yet
- 1 - Development of Practical Skills: This Does Not Include The Mean Titre Which Doesn't Have To End in 5 or 0Document1 page1 - Development of Practical Skills: This Does Not Include The Mean Titre Which Doesn't Have To End in 5 or 0Arshad KhanNo ratings yet
- 2.1 - Atoms and Reactions: 2.1.1 - Atomic Structure and IsotopesDocument13 pages2.1 - Atoms and Reactions: 2.1.1 - Atomic Structure and IsotopesArshad KhanNo ratings yet
- Solution Paper Template: Remember To Format and Save Your File As A PDF Before Uploading As Your M3 SubmissionDocument7 pagesSolution Paper Template: Remember To Format and Save Your File As A PDF Before Uploading As Your M3 SubmissionArshad KhanNo ratings yet
- Maclaurin 2017 Q OrganizedDocument13 pagesMaclaurin 2017 Q OrganizedArshad KhanNo ratings yet
- Determination of The Upper Fixed Point Physics HoDocument1 pageDetermination of The Upper Fixed Point Physics HoArshad KhanNo ratings yet
- Expressing x in terms of B, c, and MDocument1 pageExpressing x in terms of B, c, and MArshad KhanNo ratings yet
- Angle Between Two Identical Masses - Isaac PhysicsDocument1 pageAngle Between Two Identical Masses - Isaac PhysicsArshad KhanNo ratings yet
- Questionsdoppler Model Aircraftstage AllDocument1 pageQuestionsdoppler Model Aircraftstage AllArshad KhanNo ratings yet
- Angle Between Two Identical Masses - Isaac PhysicsDocument1 pageAngle Between Two Identical Masses - Isaac PhysicsArshad KhanNo ratings yet
- Research Methods BookletDocument23 pagesResearch Methods BookletArshad KhanNo ratings yet
- A Power Problem - Isaac Physics 2Document1 pageA Power Problem - Isaac Physics 2Arshad KhanNo ratings yet
- PDF ResizeDocument2 pagesPDF ResizeArshad KhanNo ratings yet
- Are Memories Really ReliableDocument40 pagesAre Memories Really ReliableArshad KhanNo ratings yet
- A-Level: Further MathematicsDocument56 pagesA-Level: Further MathematicsArshad KhanNo ratings yet
- CG - Polar Coordinates: How Can You Convert From Polar To Cartesian and Vice Versa?Document2 pagesCG - Polar Coordinates: How Can You Convert From Polar To Cartesian and Vice Versa?Arshad KhanNo ratings yet
- CJ - Numerical Methods: All of This Is in The Formula BookDocument3 pagesCJ - Numerical Methods: All of This Is in The Formula BookArshad KhanNo ratings yet
- Step 2 2015 PDFDocument12 pagesStep 2 2015 PDFVikram Guhan SubbiahNo ratings yet
- Pollution Exam QuestionsDocument5 pagesPollution Exam QuestionsArshad KhanNo ratings yet
- Step 2 2015 PDFDocument12 pagesStep 2 2015 PDFVikram Guhan SubbiahNo ratings yet
- Equality in FamiliesDocument1 pageEquality in FamiliesArshad KhanNo ratings yet
- Moles and Equations WorksheetDocument3 pagesMoles and Equations WorksheetArshad KhanNo ratings yet
- Application For Work ExperienceDocument1 pageApplication For Work ExperienceArshad KhanNo ratings yet
- Moles and Equations WorksheetDocument3 pagesMoles and Equations WorksheetArshad KhanNo ratings yet
- Presentation On: Crime Analysis and Prediction Using Data MiningDocument14 pagesPresentation On: Crime Analysis and Prediction Using Data MiningGeetika SinghNo ratings yet
- Docu98061 - VNX Operating Environment For Block 05.33.021.5.256, File 8.1.21.256 and EMC Unisphere 1.3.21.1.0256 1 Release NotesDocument122 pagesDocu98061 - VNX Operating Environment For Block 05.33.021.5.256, File 8.1.21.256 and EMC Unisphere 1.3.21.1.0256 1 Release Notesemcvilt100% (1)
- Cloud Computing Notes B Tech AKTU by Krazy Kreation (Kulbhushan)Document4 pagesCloud Computing Notes B Tech AKTU by Krazy Kreation (Kulbhushan)Pikachu Pandey100% (1)
- Zoning and Conduits For Railways - Security ArchitectureDocument59 pagesZoning and Conduits For Railways - Security Architecturemita-balijaNo ratings yet
- Review Workflow SOP and Guidelines For ITC Package Manager: BIM 360 Docs G3 Spices, GunturDocument22 pagesReview Workflow SOP and Guidelines For ITC Package Manager: BIM 360 Docs G3 Spices, GunturAakaara 3DNo ratings yet
- Microsoft Powerpoint 2010: Ali Ezojan 2 0 2 0 - C H - 2 5 2Document18 pagesMicrosoft Powerpoint 2010: Ali Ezojan 2 0 2 0 - C H - 2 5 2Ali JaffriNo ratings yet
- Android Studio: ActivityDocument8 pagesAndroid Studio: ActivityJohn J. B. NyabikoNo ratings yet
- Brave 7 AnbaDocument449 pagesBrave 7 AnbarroxoNo ratings yet
- 1080P FHD Ir PTZ CameraDocument2 pages1080P FHD Ir PTZ CameraLeonardo AravenaNo ratings yet
- UntitledDocument85 pagesUntitledFitzpatrick CunananNo ratings yet
- gTEE Whitepaper Next Generation Mission Critical NetworksDocument29 pagesgTEE Whitepaper Next Generation Mission Critical Networksahmed.hossamelden91No ratings yet
- Mobile App User Guide TemplateDocument9 pagesMobile App User Guide TemplateChrisrephot Delos ReyesNo ratings yet
- Ecen 248 Lab 4 ReportDocument5 pagesEcen 248 Lab 4 Reportapi-241454978100% (1)
- Questions About Netflix CaseDocument8 pagesQuestions About Netflix CaseMarcos Gutierrez FernandezNo ratings yet
- Fortios v6.2.5 Release NotesDocument51 pagesFortios v6.2.5 Release NotesRafael UlmusNo ratings yet
- Cloud Computing 1st Sessional Paper (30 Marks)Document12 pagesCloud Computing 1st Sessional Paper (30 Marks)Himanshu KumarNo ratings yet
- Woxen Digital Marketing Course BrochureDocument9 pagesWoxen Digital Marketing Course BrochureTanmay ChhikaraNo ratings yet
- Converge Network ServicesDocument4 pagesConverge Network ServicesGWYNETH PALLADONo ratings yet
- Teks Touch System Data EntryDocument3 pagesTeks Touch System Data Entryapi-261184918No ratings yet
- Viewsonic IFP8662 IFP62 UG ENGDocument141 pagesViewsonic IFP8662 IFP62 UG ENGpedrodiasmendesNo ratings yet
- Mathematics Diagnostic Test Class 7 Session 2021-2022Document2 pagesMathematics Diagnostic Test Class 7 Session 2021-2022Arshad BilalNo ratings yet
- Global System For Mobile Communications (GSM)Document30 pagesGlobal System For Mobile Communications (GSM)Prakash PatilNo ratings yet
- Huawei PSTN Renewal Solution 210X285mmDocument4 pagesHuawei PSTN Renewal Solution 210X285mmMohammed ShakilNo ratings yet
- HP Z400 Workstation Memory Configuration and Optimization PDFDocument1 pageHP Z400 Workstation Memory Configuration and Optimization PDFAhmedNo ratings yet
- The Documentation: (Type The Document Subtitle)Document13 pagesThe Documentation: (Type The Document Subtitle)Raghavendra KuthadiNo ratings yet
- Athena Events Rules PDFDocument9 pagesAthena Events Rules PDFHardik chughNo ratings yet
- DCA1101Document176 pagesDCA1101AWADH NARESH SINGHNo ratings yet
- 2021 01 26 DUET CSE UGP Course Curriculum A4 1Document419 pages2021 01 26 DUET CSE UGP Course Curriculum A4 1Sornali PaulNo ratings yet
- Manual HP Laptop 2Document114 pagesManual HP Laptop 2Jos LeppersNo ratings yet
- Gujarat Technological University: InstructionsDocument1 pageGujarat Technological University: InstructionsHardik PatoliyaNo ratings yet