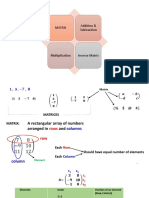
UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

Remember this...
•In symmetric
matrices, the
elements above
the diagonal is
the mirror of the
 Determinant of a Square Matrix
elements below  The determinant of a square matrix A, denoted by |A|, is a
the diagonal. polynomial of the elements of a square matrix.
 It is a scalar quantity.
 It is the sum of certain products of the elements of the
matrix from which it is derived, each product being multiplied by +1 or -1
according to certain rules.

 𝟐 × 𝟐 Matrix
𝑎 𝑎
If 𝐴 = 𝑎 𝑎 , then the determinant of A is denoted as

𝑎 𝑎
|𝐴| = 𝑎 𝑎 = 𝑎 𝑎 −𝑎 𝑎

Example 1.6. Determinant of 2×2 matrix

Find the determinant of matrix A.
3 7
|𝐴| = = 3(6) − 7(2) = 4
2 6

 𝟑 × 𝟑 Matrix

Example 1.6. Determinant of 3 ×3 matrix

Find the determinant of matrix A.
1 2 3
If 𝐴 = 4 5 6 , then the determinant of A is
7 8 9
1 2 3
|𝐴| = 4 5 6
7 8 9
5 6 4 6 4 5
= 1(+1) + 2(−1) + 2(+1)
8 10 7 10 7 8
= 1(50 − 48) − 2(40 − 42) + 3(32 − 35)

= −3
 Minors
 A submatrix multiplied to an element
 Given an element amn , its minor (denoted by |Mmn|) is obtained by deleting the mth row
and the nth column.
 The (+1) and (-1) factors in the expansion are decided according to the following rule:

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 9

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

 If A is written in the form A = (amn), the product of amn and its minor in the expansion
of determinant |A| is multiplied by (–1)m+n.
 On the given example matrix, 1 is the element 𝑎 , therefore multiplied with
(−1) = 1. Its minor is obtained by eliminating the row and column to which the
element 1 belong.

For the minor of element 1,

1 2 3
5 6
4 5 6
8 9
7 8 9

 Cofactor
 the minor multiplied with the +1 or −1 factor
5 6
Example: (+1)
8 9

 Inverse Matrix
 The inverse of a square matrix A is a matrix whose product with A is the identity matrix
Ior simply 𝑨𝑨 𝟏 = 𝑰.
 It is denoted by 𝐴 and is unique for a given matrix A.

 Adjugate / Adjoint
 denoted by adj(A)
 obtained by replacing the elements in A by their cofactors and then transposing it.
1
𝐴 = 𝑎𝑑𝑗(𝐴)
|𝐴|

Example 1.7. Inverse Matrix

Solve for the inverse of
2 5
𝐴=
3 9
SOLUTION:

The determinant of A is
2 5
det(𝐴) = = 18 − 15 = 3
3 9
Solving for the cofactors,

For 𝑎 = 2, (−1) = |9| = 9

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 10

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

For 𝑎 = 5, (−1) = |3| = −3

For 𝑎 = 3, (−1) = |5| = −5

For 𝑎 = 9, (−1) = |2| = 2

Therefore,
9 −3
𝐴=
−5 2
Then transposing to get the adjoint,
9 −5
𝑎𝑑𝑗(𝐴) =

Remember this...
−3 2
•Inverse can
So the inverse is, exist only in a
square matrix
1 9 −5 and if the
𝐴 = determinant is
3 −3 2
nonzero.

5
3 −
𝐴 = 3
2
−1 −
3

Table 1.2. Properties of Inverse

Matrix

Properties of Inverse Matrix

(𝐴𝐵) =𝐴 𝐵
(𝐴 )=𝐴
1
(𝑘𝐴) = 𝐴 k is a scalar
𝑘
𝐷 = 𝑑𝑖𝑎𝑔(𝑑 ,…𝑑 ) Dis a diagonal matrix

 Singular Matrix
 the matrix Ais said to be singular if any of the following equivalent conditions exists:
 |𝐴| = 0
 If a particular row (column) can be formed as a linear combination of the other
rows (columns)
 𝑟(𝐴) < 𝑛

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 11

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

IV. Cramer’s Rule

A method used in solving a system of linear equations. It is best applied on small
number of equations. The rule states that each unknown in a system of linear algebraic
equations may be expressed as a fraction of two determinants with denominator D and with the
numerator obtained from D by replacing the column of coefficients of the unknown in question
by the constants.

For a system of linear equations,

𝐴 𝑥+𝐵 𝑦+𝐶 𝑧 = 𝐾
𝐴 𝑥+𝐵 𝑦+𝐶 𝑧=𝐾
𝐴 𝑥+𝐵 𝑦+𝐶 𝑧=𝐾

According to the Cramer’s Rule,

𝐾 𝐵 𝐶 𝐴 𝐾 𝐶 𝐴 𝐵 𝐾
𝐾 𝐵 𝐶 𝐴 𝐾 𝐶 𝐴 𝐵 𝐾
|𝐷 | 𝐾 𝐵 𝐶 𝐷 𝐴 𝐾 𝐶 |𝐷 | 𝐴 𝐵 𝐾
𝑥= = 𝑦= = 𝑧= =
|𝐷| 𝐴 𝐵 𝐶 |𝐷| 𝐴 𝐵 𝐶 |𝐷| 𝐴 𝐵 𝐶
𝐴 𝐵 𝐶 𝐴 𝐵 𝐶 𝐴 𝐵 𝐶
𝐴 𝐵 𝐶 𝐴 𝐵 𝐶 𝐴 𝐵 𝐶

Example 1.8. Cramer’s Rule

For the following system of linear equations, solve for the values of x, y, and z.

0.3𝑥 + 0.52𝑦 + 𝑧 = −0.01

0.5𝑥 + 𝑦 + 1.9𝑧 = 0.67
0.1𝑥 + 0.3𝑦 + 0.5𝑧 = −0.44
SOLUTION:

Form a matrix using the coefficients on the left side of the equations. The determinant is
0.3 0.52 1
𝑑𝑒𝑡 = 0.5 1 1.9 = −0.0022
0.1 0.3 0.5

Solving for x, on the numerator, replace the coefficients of xby the constants k,

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 12

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

−0.01 0.52 1
0.67 1 1.9
−0.44 0.3 0.5 0.03278
𝑥= = = −14.9
−0.0022 −0.0022
Solving for y, on the numerator, replace the coefficients of y by the constants k,
0.3 −0.01 1
0.5 0.67 1.9
0.0649
𝑦 = 0.1 −0.44 0.5 = = −29.5
−0.0022 −0.0022

Solving for z, on the numerator, replace the coefficients of z by the constants k,

0.3 0.52 −0.01
0.5 1 0.67
0.1 0.3 −0.44 −0.04356
𝑧= = = 19.8
−0.0022 −0.0022
 Row-Equivalent Matrices
 Two matrices are considered to be row-equivalent if one can be obtained from the
other by a series of row operations as follows:
1. Interchange two rows. 𝑹𝒊 ⟷ 𝑹𝒋
2. Multiply a row by a nonzero constant. 𝒌𝑹𝒊 ⟶ 𝑹𝒊 (usually uses a value that
makes an element of the row equal to 1.)
3. Add a multiple of a row to another row. 𝒌𝑹𝒊 + 𝑹𝒋 ⟶ 𝑹𝒋 (usually uses a value
that makes the element below the row equal to 0.)

Example 1.9. Row-Equivalent Matrices

5 −2
Find the row-equivalent of the matrix .
2 6
SOLUTION:

Step 1. Interchange two rows. 𝑹𝟏 ⟷ 𝑹𝟐

2 6
5 −2
Step 2. Multiply a row by a nonzero constant. 𝒌𝑹𝟏 ⟶ 𝑹𝟏 .

Using 𝑘 = to make element 2 equal to 1,

1
|2 6| ⟶ |1 3|
2
Then,

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 13

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

1 3
5 −2
Step 3. Add a multiple of a row to another row. 𝒌𝑹𝟏 + 𝑹𝟐 ⟶ 𝑹𝟐

Using 𝑘 = −5 to make element 5 equal to 0,

−5|1 3| + |5 −2| ⟶ |0 −17|

Then,
1 3
0 17

 Reduced Row-Echelonform of a Matrix

 The series application of row operations transforms the matrix into its reduced row-
echelon form.
 a matrix is considered to be in reduced row-echelon form if it has the following
conditions:
1. all rows consist of all zero elements is at the bottom of the matrix
2. a row that is not all zero, has a 1 as its first nonzero element.
3. For two adjacent rows, the element 1 of the higher row must be one-step to left
of the element 1 of the lower row.
4. every column with element 1 must have all other element equal to 0.

Example 1.10. Reduced Row-Echelon Form

Find the reduced row-echelon form of the following matrix.
2 1 4
𝐴= 1 3 2
3 −1 6
SOLUTION:

Step 1. Interchange two rows. 𝑹𝟏 ⟷ 𝑹𝟐

1 3 2
2 1 4
3 −1 6

Step 2. Add a multiple of a row to another row. 𝒌𝑹𝒊 + 𝑹𝒋 ⟶ 𝑹𝒋

Using 𝑘 = −2 to make element 2of row 2 equal to 0,

𝑘𝑅 + 𝑅 ⟶ 𝑅

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 14

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

−2|1 3 2| + |2 1 4| ⟶ |0 −5 0|

Using 𝑘 = −3 to make element 3 of row 3 equal to 0,

𝑘𝑅 + 𝑅 ⟶ 𝑅
−3|1 3 2| + |3 −1 6| ⟶ |0 −10 0|
Therefore,
1 3 2
= 0 −5 0
0 −10 0

Step 3. To achieve condition 3, element -5 must be equal to 1. Multiply row 2 with − ,

1 3 2
= 0 1 0
0 −10 0
Step 4. Make other elements on column 2 equal to 0,

Using 𝑘 = −3 to make element 3 of row 1 equal to 0,

𝑘𝑅 + 𝑅 ⟶ 𝑅
−3|0 1 0| + |1 3 2| ⟶ |1 0 2|

Using 𝑘 = −10 to make element −10 of row 3 equal to 0,

𝑘𝑅 + 𝑅 ⟶ 𝑅
−10|0 1 0| + |0 −10 0| ⟶ |0 0 0|
Therefore, the reduced row-echelon form of the matrix is,
1 0 2
= 0 1 0
0 0 0

V. Gauss-Jordan Elimination
Another method of solving system of linear equations through matrices. Unlike Cramer’s
rule, Gauss-Jordan Elimination is extended to large sets of equations.

This method is variant of the Gaussian Elimination method, but unlike the method of
eliminating the unknowns and back-substitute, Gauss-Jordan Eliminationutilizes a systematic

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 15

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

process of row operations to convert the matrix into a reduced row-echelon form. Similarly, the
matrix is augmented with another column for the constant values.

Example 1.11. Gauss-Jordan Elimination

For the system of linear equations below, solve for the values of x, y, and z.

4𝑥 + 𝑦 − 𝑧 = −2
5𝑥 + 𝑦 + 2𝑧 = 4
6𝑥 + 𝑦 + 𝑧 = 6
SOLUTION:

Step 1. Generate the augmented matrix using the coefficients and constants.
4 1 −1 −2
5 1 2 4
6 1 1 6
Step 2. Normalize the first row by making element 4 equal to 1.

𝑘𝑅 ⟶ 𝑅

Using 𝑘 = ,

1
|4 1 −1 −2| ⟶ |1 0.25 −0.25 −0.5|
4
Then,
1 0.25 −0.25 −0.5
5 1 2 4
6 1 1 6
Step 3.Make other elements on column 1 equal to 0.

𝑘𝑅 + 𝑅 ⟶ 𝑅
Using 𝑘 = −5 to make element 5 of row 2 equal to 0,

−5|1 0.25 −0.25 −0.5| + |5 1 2 4| ⟶ |0 −0.25 3.25 6.5|

𝑘𝑅 + 𝑅 ⟶ 𝑅
Using 𝑘 = −6 to make element 6 of row 3 equal to 0,

−6|1 0.25 −0.25 −0.5| + |6 1 1 6| ⟶ |0 −0.5 2.5 9|

The new matrix is,

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 16

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

1 0.25 −0.25 −0.5

0 −0.25 3.25 6.5
0 −0.5 2.5 9
Step 4. Normalize the second row by making element −0.25 equal to 1.

𝑘𝑅 ⟶ 𝑅

Using 𝑘 = −4,

−4 |0 −0.25 3.25 6.5| ⟶ |0 1 −13 −26|

Then,
1 0.25 −0.25 −0.5
0 1 −13 −26
0 −0.5 2.5 9

Step 5.Make other elements on column 2 equal to 0.

𝑘𝑅 + 𝑅 ⟶ 𝑅
Using 𝑘 = −0.25 to make element 0.25 of row 1 equal to 0,

−0.25|0 1 −13 −26| + |1 0.25 −0.25 −0.5| ⟶ |1 0 3 6|

𝑘𝑅 + 𝑅 ⟶ 𝑅
Using 𝑘 = 0.5 to make element −0.5 of row 3 equal to 0,

0.5|0 1 −13 −26| + |0 −0.5 2.5 9| ⟶ |0 0 −4 −4|

The new matrix is,

1 0 3 6
0 1 −13 −26
0 0 −4 −4

Step 6. Normalize the third row by making element −4 equal to 1.

𝑘𝑅 ⟶ 𝑅

Using 𝑘 = − ,

1
− |0 0 −4 −4| ⟶ |0 0 1 1|
4

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 17

UNIVERSITY OF NUEVA CACERES COLLEGE OF ENGINEERING AND ARCHITECTURE

Then,
1 0 3 6
0 1 −13 −26
0 0 1 1

Step 7.Make other elements on column 3 equal to 0.

𝑘𝑅 + 𝑅 ⟶ 𝑅
Using 𝑘 = −3 to make element 3 of row 1 equal to 0,

−3|0 0 1 1| + |1 0 3 6| ⟶ |1 0 0 3|

𝑘𝑅 + 𝑅 ⟶ 𝑅
Using 𝑘 = 13 to make element −13 of row 2 equal to 0,

13|0 0 1 1| + |0 1 −13 −26| ⟶ |0 1 0 −13|

The new matrix is,

1 0 0 3
0 1 0 −13
0 0 1 1

x y z k

Therefore, the values of the x, y, and z are

𝑥=3
𝑦 = −13
𝑧=1

ADVANCE ENGINEERING MATHEMATICS V.1.0 BY: ART IAN G. BAUTISTA, ECE 18