Professional Documents
Culture Documents
Stone-Geary Utility Function - вывод
Uploaded by
Максим НовакOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Stone-Geary Utility Function - вывод
Uploaded by
Максим НовакCopyright:
Available Formats
Stone-Geary Utility Maximisation
Harold Walden
The corresponding video can be found at: https://youtu.be/qHZHAJozLc8
The Stone-Geary unction is often used to model problems involving subsistence levels of consumption. In these cases, a certain
minimal level of some good has to be consumed, irrespective of its price or the consumer’s income – for example; food and water.
In the two-good case, consumers will first set aside a subsidence level of consumption of the two goods; A and B of 𝛼 for good A
and 𝛽 for good B. The Stone Geary utility function is based on the traditional Cobb-Douglas utility function 𝑈 𝐴, 𝐵 = 𝐴( 𝐵)*(
where 𝛾 is the proportion of each of good A and B consumed (consequently, 𝛾 ∈ ℝ; 0 ≤ 𝛾 ≤ 1 )
As a result the Stone-Geary utility function for the two-good case can be presented as the following;
𝑈 𝐴, 𝐵 = 𝐴 − 𝛼 ( 𝐵 − 𝛽 )*(
or more simply;
𝑢 𝐴, 𝐵 = ln 𝑈 𝐴, 𝐵 = 𝛾 ln( 𝐴 − 𝛼) + (1 − 𝛾) ln 𝐵 − 𝛽
The derivation of consumer demand involving the subsistence levels of consumption involves the same method as the regular
Cobb-Douglas (maybe with a sexier standard of algebra) however, in its derivation we will yield some interesting results.
To begin with let us first set up the consumer utility optimisation problem and the resulting Lagrangian function.
Maximise: 𝑢 𝐴, 𝐵 = 𝛾 ln( 𝐴 − 𝛼) + (1 − 𝛾) ln 𝐵 − 𝛽
Subject to: 𝑀 = 𝑃< 𝐴 + 𝑃= 𝐵
Hence,
ℒ = 𝛾 ln( 𝐴 − 𝛼) + (1 − 𝛾) ln 𝐵 − 𝛽 + 𝜆 𝑀 − 𝑃< 𝐴 − 𝑃= 𝐵
Differentiating with respect to 𝐴, 𝐵 and 𝜆 yields the first order conditions:
𝑑ℒ 𝛾
= − 𝜆𝑃< = 0
𝑑𝐴 𝐴 − 𝛼
𝑑ℒ 1−𝛾
= − 𝜆𝑃= = 0
𝑑𝐵 𝐵 − 𝛽
𝑑ℒ
= 𝑀 − 𝑃< 𝐴 − 𝑃= 𝐵 = 0
𝑑𝜆
Using the first two conditions we can eliminate the Lagrangian Multiplier and find both A and B in terms of their allocation (𝛾),
their price 𝑃< , 𝑃= and their subsistence consumption (𝛼, 𝛽).
𝛾
= 𝜆𝑃<
𝐴−𝛼
1−𝛾
= 𝜆𝑃=
𝐵−𝛽
𝜆𝑃< 𝛾 𝐵−𝛽
= ×
𝜆𝑃= 𝐴 − 𝛼 1 − 𝛾
𝑃< 𝛾(𝐵 − 𝛽)
=
𝑃= (𝐴 − 𝛼)(1 − 𝛾)
𝑃< 𝐴 − 𝛼 1 − 𝛾 = 𝑃= 𝛾(𝐵 − 𝛽)
𝑃< (𝐴 − 𝛼 )(1 − 𝛾 ) = 𝑃= 𝛾 (𝐵 − 𝛽) 𝑃< (𝐴 − 𝛼 )(1 − 𝛾 ) = 𝑃= 𝛾 (𝐵 − 𝛽)
𝑃= 𝛾 (𝐵 − 𝛽) 𝑃< (1 − 𝛾 )(𝐴 − 𝛼)
𝐴−𝛼= 𝐵−𝛽 =
𝑃< (1 − 𝛾 ) 𝑃= 𝛾
𝑃= 𝛾 (𝐵 − 𝛽) 𝑃< (1 − 𝛾 )(𝐴 − 𝛼)
𝐴=𝛼+ 𝐵=𝛽+
𝑃< (1 − 𝛾 ) 𝑃= 𝛾
Bℒ
Substituting into the third condition; = 𝑀 − 𝑃< 𝐴 − 𝑃= 𝐵 = 0
BC
𝑀 = 𝑃< 𝐴 + 𝑃= 𝐵
𝑃< 1 − 𝛾 (𝐴 − 𝛼)
𝑀 = 𝑃< 𝐴 + 𝑃= 𝛽 +
𝑃= 𝛾
𝑃< 𝑃= 1 − 𝛾 (𝐴 − 𝛼) ß The 𝑃= cancel out
𝑀 = 𝑃< 𝐴 + 𝑃= 𝛽 +
𝑃= 𝛾
𝑃< 1 − 𝛾 (𝐴 − 𝛼)
𝑀 = 𝑃< 𝐴 + 𝑃= 𝛽 +
𝛾
𝑃< 1 − 𝛾 (𝐴 − 𝛼)
𝑀 − 𝑃= 𝛽 = 𝑃< 𝐴 +
𝛾
1−𝛾 ß just rearranging for neatness and to make it easier to follow
𝑀 − 𝑃= 𝛽 = 𝑃< 𝐴 + 𝑃< (𝐴 − 𝛼)
𝛾
𝑃< 𝐴 𝑃< 𝛼
𝑀 − 𝑃= 𝛽 = 𝑃< 𝐴 + − (1 − 𝛾)
𝛾 𝛾
𝑃< 𝐴 𝑃< 𝛼
𝑀 − 𝑃= 𝛽 = 𝑃< 𝐴 + − − 𝑃< 𝐴 + 𝑃< 𝛼 ß combining like terms
𝛾 𝛾
𝑃< 𝐴 𝑃< 𝛼
𝑀 − 𝑃= 𝛽 = − + 𝑃< 𝛼
𝛾 𝛾
𝑃< 𝐴 𝑃< 𝛼 (
𝑀 − 𝑃< 𝛼 − 𝑃= 𝛽 = − ß multiplying both sides of the equality by
𝛾 𝛾 EF
𝛾 𝛾 𝑃< 𝐴 𝑃< 𝛼
𝑀 − 𝑃< 𝛼 − 𝑃= 𝛽 = −
𝑃< 𝑃< 𝛾 𝛾
𝛾
𝑀 − 𝑃< 𝛼 − 𝑃= 𝛽 = 𝐴 − 𝛼
𝑃<
Therefore the Marshallian Demand Function for Good A is;
𝛾
𝐴D = 𝛼 + 𝑀 − 𝑃< 𝛼 − 𝑃= 𝛽
𝑃<
and by symmetry, the Marshallian Demand Function for Good B is;
1−𝛾
𝐵D = 𝛽 + 𝑀 − 𝑃< 𝛼 − 𝑃= 𝛽
𝑃=
Important points to take away from this derivation:
- Each of the functions of 𝐴D and 𝐵 D are the Marshallian demand functions for the Stone-Geary utility.
- The first term on the right-hand-side of the equality, is the subsistence consumption. A consumer will always consume
this amount irrespective of their budgets or the price.
- The 𝑀 − 𝑃< 𝛼 − 𝑃= term is the income the consumer has left over, after the subsistence levels are met. It is in effect, the
residual income.
- The amount of A and B that this residual income is used to buy, is now negatively influenced by price, and positively
influenced by the good’s importance. For instance, if γ increases, it implies that good A is relatively more important than
B. According to these demand functions, our consumer will purchase less of B and more of A, all other things equal.
Hope it helps J
Harold
You might also like
- 1st Grading Lesson 5 - GR 9Document9 pages1st Grading Lesson 5 - GR 9justanotherbroadwayfanNo ratings yet
- Board Questions - DifferentiabilityDocument14 pagesBoard Questions - DifferentiabilitySai tejaNo ratings yet
- The Value ChainDocument6 pagesThe Value ChainFabio Hernan TorresNo ratings yet
- Resistencia de Materiales 2Document23 pagesResistencia de Materiales 2Anyela Sedano QuispeNo ratings yet
- Board Questions - ContinuityDocument9 pagesBoard Questions - Continuityadityaaaaaa002No ratings yet
- 19-03-2023Document37 pages19-03-2023Praveen praveenNo ratings yet
- Ciclo Rankine y Brayton con regeneracionDocument1 pageCiclo Rankine y Brayton con regeneracionMilton SteevenNo ratings yet
- (201552020012) Ilham Aulia Amanullah Statistika Tugas 8Document7 pages(201552020012) Ilham Aulia Amanullah Statistika Tugas 8Islami Farhan SyahputraNo ratings yet
- A. B. C. D.Document7 pagesA. B. C. D.Islami Farhan SyahputraNo ratings yet
- Investments Key FormulasDocument1 pageInvestments Key FormulasMICHAEL haikenNo ratings yet
- Resumen Ecuaciones Temas 5, 6 y 7 PDFDocument3 pagesResumen Ecuaciones Temas 5, 6 y 7 PDFScottyNo ratings yet
- Formulario Administración Integral de YacimientosDocument3 pagesFormulario Administración Integral de Yacimientostomhands07No ratings yet
- 1.1 Hard Margin SVM (Insert Diagrams)Document4 pages1.1 Hard Margin SVM (Insert Diagrams)shabaazkurmally.um1No ratings yet
- Armand File WAG DELETEDocument3 pagesArmand File WAG DELETERay Armand GappiNo ratings yet
- Reac Ii 2023 CH 4Document37 pagesReac Ii 2023 CH 4hagt813No ratings yet
- 2 3 Evaluating Functions Operation Composition of FunctionsDocument42 pages2 3 Evaluating Functions Operation Composition of FunctionsClowohNo ratings yet
- Differentiation Rules For Algebraic Functions Higher Order Derivatives Optimization ProblemsDocument29 pagesDifferentiation Rules For Algebraic Functions Higher Order Derivatives Optimization ProblemsAntonio OngNo ratings yet
- Formulario U3Document2 pagesFormulario U3MexahopNo ratings yet
- 5Document6 pages5Yas MonazahNo ratings yet
- 18IntegrationTechniquesDocument18 pages18IntegrationTechniquesأيوب عبد الأمير هزبر /تقنية غازNo ratings yet
- 27 RMM Winter Edition 2022 SolutionsDocument92 pages27 RMM Winter Edition 2022 SolutionsCesar Villalta CuetoNo ratings yet
- 18ME54 Turbo Machines Module 03 Question No 6a & 6bDocument9 pages18ME54 Turbo Machines Module 03 Question No 6a & 6bThanmay JSNo ratings yet
- Deriving Almansi Strain in Terms of DisplacementDocument2 pagesDeriving Almansi Strain in Terms of DisplacementJohn Mark Go PayawalNo ratings yet
- 55caa95sye Structural analysis equationsDocument2 pages55caa95sye Structural analysis equationsAnonymous wrsmp5hEWNo ratings yet
- SDFSDFSDDocument5 pagesSDFSDFSDElyssa JaneNo ratings yet
- Lecture 4Document8 pagesLecture 4Abdalla NasserNo ratings yet
- 2.3 Diesel CycleDocument15 pages2.3 Diesel CycleSan Jose, Kyla Mae M.No ratings yet
- PH4Document4 pagesPH4za3iman12No ratings yet
- EE435 - Chapter5 - Lec1 - Transient Response Analysis - Part A - A.HaddadDocument20 pagesEE435 - Chapter5 - Lec1 - Transient Response Analysis - Part A - A.HaddadIbrahim abdoNo ratings yet
- 10 Higuera Corrosion y TransporteDocument49 pages10 Higuera Corrosion y TransporteEduardo SorcererNo ratings yet
- Caida LibreDocument12 pagesCaida Librefredy chozo tunoqueNo ratings yet
- TM CM L11 4 PDFDocument1 pageTM CM L11 4 PDFsayandatta1No ratings yet
- C 1906634 U226385 s977868Document50 pagesC 1906634 U226385 s977868royalNo ratings yet
- Ut FSMDocument147 pagesUt FSMCarito SPNo ratings yet
- Formulas Obs ESPDocument1 pageFormulas Obs ESPw4zv8w2b74No ratings yet
- Chapter 11Document122 pagesChapter 11Rozin FaruqNo ratings yet
- RMM GEOMETRY MARATHON 401 500 - CompressedDocument131 pagesRMM GEOMETRY MARATHON 401 500 - CompressedHarshul NandaNo ratings yet
- Quantitative Methods SYMBOL of SUM, Double SUM and MultiplicationDocument24 pagesQuantitative Methods SYMBOL of SUM, Double SUM and MultiplicationCasper DarkusNo ratings yet
- Constructing a Concrete Trinomial Tree ModelDocument4 pagesConstructing a Concrete Trinomial Tree ModelAbdullah AbdullahNo ratings yet
- Stiffness 1Document31 pagesStiffness 1ahmed elgendyNo ratings yet
- Formulario N 1 (Algebra)Document1 pageFormulario N 1 (Algebra)Moises Mamani BarcoNo ratings yet
- Solving Systems of Linear Differential Equations by EliminationDocument10 pagesSolving Systems of Linear Differential Equations by EliminationReinaNo ratings yet
- Ex 2 Two Hinge ArchDocument3 pagesEx 2 Two Hinge ArchchandrasekarNo ratings yet
- PrimalformDocument3 pagesPrimalformAdam FaisalNo ratings yet
- Formulari 2023-24Document2 pagesFormulari 2023-24agraciabalaguerNo ratings yet
- International Refereed Journal of Engineering and Science (IRJES)Document8 pagesInternational Refereed Journal of Engineering and Science (IRJES)www.irjes.comNo ratings yet
- Formulae All in OneDocument18 pagesFormulae All in Onemysteriousmbj20No ratings yet
- Regla de la cadena matemática IIDocument57 pagesRegla de la cadena matemática IIEduin JiménezNo ratings yet
- Gmb105 Business Statistics/Mathematics FormulaeDocument2 pagesGmb105 Business Statistics/Mathematics FormulaeLashierNo ratings yet
- Generator _ Load ModellingDocument3 pagesGenerator _ Load ModellingYoussef EzatNo ratings yet
- Single Side Band Modulation SSBDocument23 pagesSingle Side Band Modulation SSBHariprasad VolluriNo ratings yet
- Problem Set 2 - AnswersDocument5 pagesProblem Set 2 - Answersdxd032No ratings yet
- Worksheet Solution 4Document8 pagesWorksheet Solution 4abdelrahmanhelal13No ratings yet
- BASCALQ4Document5 pagesBASCALQ4Marjuline De GuzmanNo ratings yet
- JawabDocument2 pagesJawabAchdanNo ratings yet
- Steady state error and control system conceptsDocument4 pagesSteady state error and control system conceptsAhmed KhaledNo ratings yet
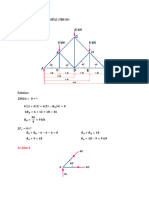
- CE100 Module 3 Example (Truss)Document4 pagesCE100 Module 3 Example (Truss)Stephanie Jean Magbanua CortezNo ratings yet
- Instructor's Manual to Accompany CALCULUS WITH ANALYTIC GEOMETRYFrom EverandInstructor's Manual to Accompany CALCULUS WITH ANALYTIC GEOMETRYNo ratings yet
- Relative Valuation - Accuracy of Corporate ValDocument36 pagesRelative Valuation - Accuracy of Corporate ValSriramShettyNo ratings yet
- Регрессия хор модель кросс-секция ИндонезияDocument14 pagesРегрессия хор модель кросс-секция ИндонезияМаксим НовакNo ratings yet
- Predicting Valuation Multiples (Master TH)Document142 pagesPredicting Valuation Multiples (Master TH)Максим НовакNo ratings yet
- 12 - Does Education Influence IncarcerationDocument1 page12 - Does Education Influence IncarcerationМаксим НовакNo ratings yet
- Band 9 MapDocument1 pageBand 9 MapМаксим НовакNo ratings yet
- Charging Electric Vehicles - Best Practice Guide-WEBDocument34 pagesCharging Electric Vehicles - Best Practice Guide-WEBМаксим НовакNo ratings yet
- How To Compare Valuation MethodsDocument41 pagesHow To Compare Valuation MethodsМаксим НовакNo ratings yet
- Research Repository Version - 16.08.2019Document658 pagesResearch Repository Version - 16.08.2019Максим НовакNo ratings yet
- Key Terms of Social Inequality GlossaryDocument2 pagesKey Terms of Social Inequality GlossaryМаксим НовакNo ratings yet
- Сем 3 (задание 1)Document18 pagesСем 3 (задание 1)Максим НовакNo ratings yet
- HW Tapescript - The Age-Old Sharing Economies of Africa - and Why We Should Scale ThemDocument5 pagesHW Tapescript - The Age-Old Sharing Economies of Africa - and Why We Should Scale ThemМаксим НовакNo ratings yet
- CH 9. Endowement Bying and SellingDocument45 pagesCH 9. Endowement Bying and SellingМаксим НовакNo ratings yet
- Digital Economy and EducationDocument2 pagesDigital Economy and EducationМаксим НовакNo ratings yet
- Two Hopeless Causes: Education and IncarcerationDocument37 pagesTwo Hopeless Causes: Education and IncarcerationМаксим НовакNo ratings yet
- Rečka - Elasticity of SubstitutionDocument10 pagesRečka - Elasticity of SubstitutionМаксим НовакNo ratings yet
- What Is Implied by The Tax-Free World/countries? Can Contemporary Economies ( Countries) Exist Without Taxation?Document3 pagesWhat Is Implied by The Tax-Free World/countries? Can Contemporary Economies ( Countries) Exist Without Taxation?Максим НовакNo ratings yet
- 4 - 1. Glossary of Behavioural Economics TermsDocument5 pages4 - 1. Glossary of Behavioural Economics TermsМаксим НовакNo ratings yet
- Endowment ModelDocument8 pagesEndowment ModelBristena Maria OprisanuNo ratings yet
- Guide To Sharing EconomyDocument61 pagesGuide To Sharing EconomyМаксим НовакNo ratings yet
- Key Figures in EuropeDocument79 pagesKey Figures in EuropeМаксим НовакNo ratings yet
- Econ11 HW PDFDocument207 pagesEcon11 HW PDFAlbertus MuheuaNo ratings yet
- Consumer Choice Indifference CurvesDocument27 pagesConsumer Choice Indifference CurvesМаксим НовакNo ratings yet
- Spreadsheet Modeling & Decision Analysis:: A Practical Introduction To Management Science, 3eDocument69 pagesSpreadsheet Modeling & Decision Analysis:: A Practical Introduction To Management Science, 3eМаксим НовакNo ratings yet
- What Is The Sharing Economy - Example Companies, Definition, Pros & ConsDocument11 pagesWhat Is The Sharing Economy - Example Companies, Definition, Pros & ConsМаксим НовакNo ratings yet
- Stone GearyDocument2 pagesStone GearyМаксим НовакNo ratings yet
- Utility Theory Dominic SalDocument30 pagesUtility Theory Dominic SalMahin1977No ratings yet
- Utility Theory Dominic SalDocument30 pagesUtility Theory Dominic SalMahin1977No ratings yet
- Chapter 14 Bond Prices and Yields (Slide)Document104 pagesChapter 14 Bond Prices and Yields (Slide)Giang Nguyễn LêNo ratings yet
- Summary FunctionsDocument3 pagesSummary FunctionsJamesLastNo ratings yet
- CHAPTER 6lesson 4Document11 pagesCHAPTER 6lesson 4Leandro Ulysis Tayco OronganNo ratings yet
- Herrmann Brain Dominance Instrument Thinking Styles AssessmentDocument6 pagesHerrmann Brain Dominance Instrument Thinking Styles AssessmentVincentFozzNo ratings yet
- Java Lab Exercise - 6Document5 pagesJava Lab Exercise - 6Dhanush DhoniNo ratings yet
- 115 Sample Chapter PDFDocument111 pages115 Sample Chapter PDFAmey GudigarNo ratings yet
- Introduction To Hypothesis TestingDocument16 pagesIntroduction To Hypothesis TestingYaha RewNo ratings yet
- Chapter 2 Fundamental Simulation ConceptsDocument50 pagesChapter 2 Fundamental Simulation ConceptsHrishikesh WaghNo ratings yet
- 2009T1Document8 pages2009T1smk1992No ratings yet
- MX3D BridgeDocument7 pagesMX3D BridgeJanko Vukicevic100% (1)
- Chap 15ha OscillationsDocument61 pagesChap 15ha OscillationsXahid HasanNo ratings yet
- Rajasthan Technical University B.Tech SyllabusDocument8 pagesRajasthan Technical University B.Tech SyllabusAmit BagrechaNo ratings yet
- Mathematics Grade 10 Term 1 Week 5 - 2021Document8 pagesMathematics Grade 10 Term 1 Week 5 - 2021martinajoan1No ratings yet
- Roadmap For Quant 1705217537Document10 pagesRoadmap For Quant 1705217537VaibhavNo ratings yet
- AQA A Level Mathematics Year 2 Sample Chapters PDFDocument64 pagesAQA A Level Mathematics Year 2 Sample Chapters PDFswatiNo ratings yet
- 7 19 Updated Grade 11 Students Online Schedule 2021 2022 1st SemDocument8 pages7 19 Updated Grade 11 Students Online Schedule 2021 2022 1st SemAngelo MartinezNo ratings yet
- Acoustics: EE E6820: Speech & Audio Processing & RecognitionDocument32 pagesAcoustics: EE E6820: Speech & Audio Processing & RecognitionevilasionsNo ratings yet
- CHAPTER 5 SemiconductorsDocument42 pagesCHAPTER 5 Semiconductors1553No ratings yet
- Class - 8 - NSTSE - MQP - 436 (M) & 439 (M) PDFDocument16 pagesClass - 8 - NSTSE - MQP - 436 (M) & 439 (M) PDFMADHAWI CHOUDHARYNo ratings yet
- Report-On-National-Seminar Exploring Physics With ExpertsDocument7 pagesReport-On-National-Seminar Exploring Physics With ExpertsShikha sharmaNo ratings yet
- Lighthouse Institute Mathematics Cala D 2023Document4 pagesLighthouse Institute Mathematics Cala D 2023Kudakwashe RushwayaNo ratings yet
- Fast CountDocument5 pagesFast CountMcan AlkanNo ratings yet
- Novel Approach to Job's MethodDocument6 pagesNovel Approach to Job's Methodiabureid7460No ratings yet
- Simple Harmonic MotionDocument17 pagesSimple Harmonic MotionChirag Hablani100% (1)
- POLYNOMIALS Puzzle 1Document1 pagePOLYNOMIALS Puzzle 1Sekhar Reddy100% (1)
- Barcelo - Computational Intelligence in ArchaeologyDocument437 pagesBarcelo - Computational Intelligence in Archaeologyhristijan_anch100% (1)
- Belt DesignDocument27 pagesBelt DesignshubhamNo ratings yet
- Mcob Unit-2Document44 pagesMcob Unit-2Sharma GsrNo ratings yet
- Notes On Vectors and PlanesDocument10 pagesNotes On Vectors and PlanesParin ShahNo ratings yet
- Optimum Design of Reinforced Concrete Rectangular Beams Using Simulated AnnealingDocument10 pagesOptimum Design of Reinforced Concrete Rectangular Beams Using Simulated AnnealingAndripgaNo ratings yet
- ASCE 7-22 CH 26com - For PC - SouDocument116 pagesASCE 7-22 CH 26com - For PC - SousharethefilesNo ratings yet
- Double and Triple Integration in Polar CoordinatesDocument25 pagesDouble and Triple Integration in Polar CoordinatesLol KekNo ratings yet