1656_C02.

fm Page 93 Thursday, April 14, 2005 6:28 PM

Linear Elastic Fracture Mechanics 93

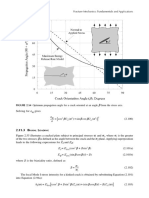
FIGURE A2.1 Plate corner configuration analyzed by Williams. A crack is formed when ψ = 2π : (a) plate
corner with included angle ψ and (b) special case of a sharp crack. Taken from Williams, J.G. and Ewing,
P.D., International Journal of Fracture Mechanics, Vol. 8, 1972.

For the configuration shown in Figure A2.1(b), Williams postulated the following stress function:

[
Φ = r λ +1 c1 sin (λ + 1)θ * + c2 cos(λ + 1)θ + c3 sin(λ − 1)θ * + c4 cos(λ − 1)θ *
*
]
= r λ +1Φ(θ * , λ ) (A2.19)

where c1, c2, c3, and c4 are constants, and θ * is defined in Figure A2.1(b). Invoking Equation (A2.13)
gives the following expressions for the stresses:

σ rr = r λ −1[ F ′′(θ * ) + (λ + 1) F(θ * )] (A2.20a)

σ θθ = r λ −1[λ (λ + 1) F(θ * )] (A2.20b)

τ rθ = r λ −1[− λF ′(θ * )] (A2.20c)

where the primes denote derivatives with respect to θ*. Williams also showed that Equation (A2.19)
implies that the displacements vary with r λ. In order for displacements to be finite in all regions of the
body, λ must be > 0. If the crack faces are traction free, σ θθ (0) = σ θθ (2π ) = τ rθ (0) = τ rθ = (2π ) = 0,
which implies the following boundary conditions:

F(0) = F(2π ) = F ′(0) = F ′(2π ) = 0 (A2.21)

Assuming the constants in Equation (A2.19) are nonzero in the most general case, the boundary
conditions can be satisfied only when sin(2πλ ) = 0 . Thus,

n
λ = , where n = 1, 2, 3,…
2
There are an infinite number of λ values that satisfy the boundary conditions; the most general
solution to a crack problem, therefore, is a polynomial of the form
N n
 n 
∑  r Fθ * ,  
+1
Φ= 2 (A2.22)
 2
n =1