64 Power Electronics and Control Techniques for Maximum Energy Harvesting

96
MPP

94 X2 X3
PV Power [W]

92

90

88
X1
∆VPV ∆VPV
86

84
13 14 15 16 17 18 19
PV Voltage [V]

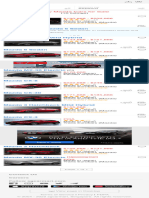
Figure 2.19
Operating points location on PV characteristic.

operating points across the MPP. The unbalanced position of the operating
points across the MPP, which can occur if any perturbative MPPT approach
is used, has a detrimental effect on the MPPT efficiency, and thus it must be
corrected properly.
In a fixed step size P&O algorithm, the discretized value of Δx usually
does not allow us to have a three-point steady-state behavior with a central
point close to the MPP and the other two equally balanced at its sides. A very
common situation is that shown in Figure 2.19, where the operating points
x1, x 2, and x 3 are equally spaced in terms of PV voltage, but they are not well
balanced with respect to the MPP.
The lower Δx, the lower the distance between x 2 and the MPP. The non-
symmetrical position of the three operating points is less efficient than the
balanced condition, occurring when ×2 is centered in MPP with x1 and x3
equally spaced in terms of PV voltage, and it might also trigger a four-point
oscillation, with a further increase of the power loss. A four-point oscilla-
tion obtained in an experimental case is shown in Figure 2.20. A sequence
of seven operating points around the MPP of the P&O algorithm is plotted.
If the position of the operating points is asymmetric with respect to the
MPP, the points that are closer to the MPP (x 2 and x 3 in Figure 2.19) have
more or less the same power level. In the presence of noise and round-
ing errors introduced by the measurement system, the action of the MPPT
algorithm might be wrong. For instance, when the operating point jumps
from position 5 to 6, due to noise or slight variations of the irradiance level,
the measured value of the PV power might be different from that evalu-
ated in point 2. As a consequence, ΔP has a sign that causes an additional
step in the wrong direction (1 = 7). By comparing the real sequence (1-2-3-4)