would the Bureau conclude about the operation of

the local firm?

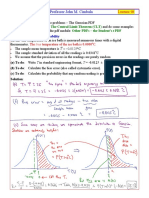
ACTIVITY 12 CLAIM: An investigating of several complaints
concerning the weight of the “NET WT. 12 0z” jar
Test of Hypothesis of a local brand of peanut is less than this value.
I. Ho: μ = 12
Solve for the following problems. Follow the steps in
testing the hypothesis. H1: μ > 12
II. Level of significance: α = 0.01

1.) It is claimed It is claimed that an automobile is III. Type of test: Z - Test

driven on the average more than 20,000
kilometers per year. To test this claim, a random
sample of 100 automobile owners are asked to IV. Critical Region: 2.33 (one-tailed)
keep a record of the kilometers they travel. Would
you agree with this claim if the random sample
V. Test Statistic: =
̅
showed an average of 23,500 kilometers and a /√
standard deviation of 3900 kilometers? Use α = .
= .
0.05 in your conclusion.
√
= -1.6
CLAIM: An automobile is driven on average VI. DECISION: We accept the null hypothesis.
more than 20,000 kilometers per year.
VII. CONCLUSION:
I. Ho: μ = 20,000 Ho is accepted therefore the weight of the peanut
butter jar is less than 12.0 oz.
H1: μ > 20,000

II. Level of significance: α = 0.05

3.) The Edison Electric Institute has published figures
on the annual number of kilowatt hours expended
III. Type of test: Z - Test by various home appliances. It is claimed that a
vacuum cleaner expends an average of 46 kilowatt
hours per year. If a random sample of 12 homes
IV. Critical Region: t > 1.645 (one-tailed) included in a planned study indicates that vacuum
cleaners expend an average of 42 kilowatt hours
per year with a standard deviation of 11.9 kilowatt
hours, does this suggest at the 0.05 level of
V. Test Statistic: =
̅
/√ significance that vacuum cleaners expend, on the
, , average, less than 46 kilowatt hours annually?
=
√
Assume the population of kilowatt hours to be
= . normally distributed with α = 0.01
VI. DECISION: Reject the null hypothesis CLAIM: A vacuum cleaner expends an
average of 46 kilowatt hours per year.
VII. CONCLUSION: I. Ho: μ = 46
Vehicles are driven more than 20,000
km/year. H1: μ < 46
II. Level of significance: α = 0.05

III. Type of test: T - Test

2.) An investigating several complaints concerning
the weight of the “NET WT. 12 0z” jar of a local IV. Critical Region: =− , =− . ,
brand of peanut is less than this value. The
Better Business bureau selected a sample of 36 = 11
jars. The sample showed an average net weight of
11.92 ounces and a standard deviation of 0.3
ounce. Using a 0.01 level of significance, what
 V. Test Statistic: =
̅ VII. CONCLUSION:
/√ The level of significance of the car advertisement
= . is greater than 0.005.
√
= − .
VI. DECISION: Accept the null hypothesis. 5.) A random sample of size n1 = 25, taken from a
normal population with a standard deviation σ1 =
VII. CONCLUSION:

The average number of kW/hr of a vacuum
cleaner is less than 46 kW/hr. 5.2, has a mean x1 = 81. A second random
sample of size n2 = 36, take from a normal
population with a standard deviation σ1 = 3.4, has
4.) A car is advertised as having a gas mileage rating 

of at least 30 miles per gallon. If the miles per a mean x 2 = 76. Test the hypothesis than μ1 =
gallon in 10 independent experiments are 26, 24, μ2 against the alternative, μ1 ≠ μ2. Use a 0.05
20, 25, 27, 25, 28, 30, 26, 33, should you believe level of significance.
the advertisement? Use 0.05 & 0.01 level of
significance. CLAIM: To test the hypothesis than µ =
µ against the alternative, µ ≠ µ .
A. CLAIM: A gas mileage rating of the car in a
I. Ho: µ − µ = 0
highway driving in a normal distribution.
I. Ho: μ ≥ 30 H1: µ − µ ≠ 0

H1: μ < 30 II. Level of significance: α = 0.05

II. Level of significance: α = 0.05 III. Type of test: Z – Test
III. Type of test: T - Test IV. Critical Region:
IV. Critical Region: T9 > −1. 833 Z< . or Z > .
± 1.96 (two tailed test)
V. Test Statistic:
V. Test Statistic:
p= [ √ < √ ] Z=
( ̅ ̅ )
√
.
p= [ √ < √10 .
]
( )
p = P = (T < 3.251) = 0.005 Z=
( . ) ( . )
VI. DECISION: Reject the null hypothesis.
VII. CONCLUSION:
Z=
√ . .
The level of significance of the car advertisement Z = 4.22
is greater than 0.005. VI. DECISION: We reject the null hypothesis.

B. CLAIM: A gas mileage rating of the car in a VII. CONCLUSION:

highway driving in a normal distribution. The result is less than the common
I. Ho: μ ≥ 30 significant level of 0.05.

H1: μ < 30
II. Level of significance: α = 0.01
III. Type of test: T - Test

IV. Critical Region: T9 > −1. 833

V. Test Statistic:
p= [ √ < √ ]
√
.
p= [ √ < √10 ]
.
p = P = (T < 3.251) = 0.005
VI. DECISION: Reject the null hypothesis.