Professional Documents
Culture Documents
CS Stability Control T
Uploaded by
Prasun SinghalOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
CS Stability Control T
Uploaded by
Prasun SinghalCopyright:
Available Formats
Control Systems (Stability)
Stability
Objective
Upon completion of this chapter you will be able to:
Characterize the system in terms of stable, unstable and marginally stable.
Calculate the number of poles of closed loop system in left half plane, right half plane
and on the imaginary axis.
Calculate the range of the gain of open loop system for stability of closed loop
system.
Analyse relative stability of a control system.
Introduction
Among the many forms of performance specifications used in the design of control system,
the most important requirement is that system must be stable at all times. Stability in a
system implies that small changes in input, in initial condition or system parameters do not
result in large changes in system output. A stable system if disturbed from its equilibrium
position returns to its original state eventually after disturbance is removed. As for an
example when pendulum is disturbed from its original position by a small amount it exhibits
damped oscillations about mean position and finally settles down to original mean position.
Criterion for Stability
A linear – time invariant system is stable if following two notions of stability are satisfied:
a) When the system is excited by bounded input the output is bounded. BIBO
b) In the absence of input, output tends towards zero (the equilibrium state of system)
irrespective of initial conditions; this is called as asymptotic stability. An example of
asymptotically stable system is discharging RC circuit where voltage across capacitor is
eventually reduced to zero.
If the system is excited by unbounded inputs & output is also unbounded then nothing
can be said about its stability.
© Kreatryx. All Rights Reserved. 1 www.kreatryx.com
Control Systems (Stability)
Consider a single i/p, single o/p system with a transfer function.
C s b sm b sm 1 ............b
G s 0 1 m
R s n
a s a s n 1 ...............a
0 1 n
Initial conditions are assumed to be zero.
c t L1 G s R s
c t g r t d
0
g L1 G s is impulse response of system
Take absolute value both sides
c t g r t d
0
Since absolute value of integral is always less than integral of absolute value.
c t g r t d
0
For bounded input r t M
1
c t M g d M
1 2
0
Which means that output is bounded which is the criteria for BIBO stability.
First notion of stability is satisfied if g(t) is absolutely integrable.
i.e. g d is finite
0
This is the criterion for BIBO stability.
© Kreatryx. All Rights Reserved. 2 www.kreatryx.com
Control Systems (Stability)
Relation between locations of roots & stability
When all roots characteristics equation lie in left half plane the system response due to
initial conditions will decrease to zero as time approaches infinity.
If one or more pairs of simple roots lie on imaging axis of s – plane but there are no roots
in RHP the response to initial conditions is un damped sinusoidal oscillations.
If one or more roots are found in right half of s – plane, the response increases in
magnitude as time increases.
Pole Location Stability Impulse Response
1 Absolutely Stable
F s
sa
1 Absolutely Stable
F s
s a2
1 Absolutely Stable
F s
2
s a b2
1 Marginally
F s
s or critically stable
1 Marginally
F s
s2 a2 or critically stable
© Kreatryx. All Rights Reserved. 3 www.kreatryx.com
Control Systems (Stability)
1 Unstable
F s
2
s2 a2
1 Unstable
F s
sa
1 Unstable
F s
s a2
1 Unstable
F s
2
s a b2
Conditions for stability
The necessary (but not sufficient) condition for stability of a linear system is that all
coefficients of its characteristics equation (q(s) = 0) be real & have same sign. Furthermore,
none of the coefficients should be zero.
1) The positiveness of the coefficients of the characteristics equation is necessary &
sufficient condition for the stability of the system of first & second order.
© Kreatryx. All Rights Reserved. 4 www.kreatryx.com
Control Systems (Stability)
The characteristics equation of a first order system is
a sa 0
0 1
a
which has single root, s 1
a
0
For second order system,
a s2 a s a 0
0 1 2
2
a1 a1 4a0 a2
Which has roots s ,s
1 2 2a
0
2) The positiveness of the coefficients of characteristic equation ensures the negativeness of
the real roots but does not ensures the negativeness of the real parts of the complex roots
for third & higher order systems.
3 2
As for an example for the following Characteristic Equation: s s 2s 8 0 , the roots are
15 15
given by s 2 s 0.5 j s 0.5 j 0
2 2
Real parts of the complex roots is positive indicating instability of the system even though all
the coefficients of characteristics equation are positive.
Routh – Hurwitz Method
The criterion is based on ordering the coefficients of the characteristics equation into an
array called Routh Array as given below:
Example: P s s4 8s3 18s2 16s 5 0
Routh Array
s4 1 18 5
s3 8 16 0
s2 b 16 b 5
1 2
s1 C 13.5 0
1
s0 d 5
1
© Kreatryx. All Rights Reserved. 5 www.kreatryx.com
Control Systems (Stability)
8 18 16 85 0 16 16 40
b 16 ; b 5 ; C 13.5 ;
1 8 2 8 1 16
13.5 5 16 0
d 5
1 13.5
Since denominator always coefficients from the 1st column, the sign changes of only the
first column are considered.
Since there are no sign changes in the first column of Routh Array, so there are no roots
of the characteristic equation lying in the right half plane.
Number of poles in RHP = Number of Sign Changes in first column of Routh Array
Number of poles in LHP = Order of Characteristic Equation – Number of Poles in RHP
So, in this case all 4 poles lie in LHP and system is stable.
Solved Examples
Problem: Find the number of poles in right half plane for the system whose characteristic
4 3 2
equation is 3s 10s 5s 5s 2 0
Solution: Routh Array
s4 3 5 2
s3 10 5
s3 2 1 Dividing this row by 5 through out
s2 3.5 2
s1 0.5
3.5
s0 2
Examining first column of Routh array, that there are two changes in sign (from 3.5 to 0.5 3.5
0.5
& from to 2)
3.5
Hence, there are 2 poles of the system lying in the Right Half Plane.
© Kreatryx. All Rights Reserved. 6 www.kreatryx.com
Control Systems (Stability)
Special Cases
Case 1: When the first element of any row is zero while the rest of the row has at least one
non – zero term, in such cases substitute a small positive number ‘ ’ in place of zero &
evaluate the rest of the Routh Array in terms of . Check for sign changes in the first column
by taking limit 0 to comment on stability.
3 2
As for an example for the characteristic equation: s 2s s 2 0 , the routh array will be
as shown below:
s3 1 1
s2 2 2
s1
s0 2
If the sign of the coefficient above the zero is same as that below it, if indicates that
there are a pair of imaginary roots.
Case 2: When Routh Array ends abruptly i.e. all elements in any one row is zero, construct an
auxiliary equation A(s), differentiate if to get new coefficients & evaluate the roots of the
Routh Array. Check the roots of auxiliary equation for roots on jω axis to comment on
stability.
The Routh array for the following Characteristic Equation would look like:
s6 2s5 8s4 12s3 20s2 16s 16 0
Routh array
s6 1 8 20 16
s5 2 12 16
s5 1 6 8
s4 2 12 16
s4 1 6 8
s3 0 0
© Kreatryx. All Rights Reserved. 7 www.kreatryx.com
Control Systems (Stability)
3
Since terms of s are all zero, the Routh’s test break down. We form auxiliary equation using
the elements in the row preceding the row consisting of all zeroes.
Auxiliary equation A s s4 6s2 8
dA s
Derivative w.r.t. s => 4s3 12s
ds
s6 1 8 20 16
s5 1 6 8
s4 1 6 8
s3 4 12
s3 1 3
s2 3 8
s1 13
s0 8
There are no sign changes in first column of new array.
By solving roots of auxiliary polynomial.
s4 6s2 8 0 => s j 2 , j2
So, system is marginally stable.
Properties of Auxiliary Equation
The roots of auxiliary equation are always symmetrical about y – axis.
The number of sign changes below the row of auxiliary equation gives number of
RHP of auxiliary equation & by symmetry, same number of poles exist in LHP.
No. of poles on imaginary axis = Order of AE – 2* Number of Sign changes below AE
Total no. of poles in RHP = Total no. of sign changes in RHP
Total number of poles in LHP = Order of Characteristic Equation – Number of poles
on imaginary axis – Number of poles in RHP
© Kreatryx. All Rights Reserved. 8 www.kreatryx.com
Control Systems (Stability)
Solved Examples
Problem: Identify the number of poles in left half plane, right half plane and on the
imaginary axis for the system whose transfer function is given below:
s2 7s 10
T s
s6 2s4 s2 2
Solution: Routh Array for the system given above is shown below:
s6 1 2 1 2
s5 0 0 0
6
So AE s 2s s 2
4 2 (order = 6)
Hence, 6 symmetrical poles
d
AE 6s5 8s3 2s
ds
s6 1 2 1 2
s5 6 8 2
s5 3 4 1
s4 2
3
2
3 2
s4 1
3
1
3 1
s3 7 8
s2 5
7 1
s1 9
5
s0 1
So 1 sign change & hence 1 pole in RHP & by summitry 1 pole in LHP.
So remaining 4 poles lie on imaginary axis.
© Kreatryx. All Rights Reserved. 9 www.kreatryx.com
Control Systems (Stability)
Problem: Identify the number of poles in left half plane, right half plane and on the
imaginary axis for the system whose characteristic equation is given below:
s4 s3 3s2 s 2 0
Solution: The Routh Array for the given Characteristic Equation looks like:
s4 1 3 2
s3 1 1
s2 2 2
s1 0
2
The Auxiliary Equation becomes A(s) = 2s 2
dA(s)
The derivative of Auxiliary Equation is given by: 4s
ds
Now, the Routh Array becomes
s4 1 3 2
s3 1 1
s2 2 2
s1 4
s0 2
Number of sign changes below AE = 1 so there are 2 symmetrical poles one in LHP and
other in RHP.
Number of Poles on Imaginary Axis = 2 – 2*1 = 0
Total Number of Sign Changes = Total number of poles in RHP = 2
Number of poles in LHP = 4 – 2 – 0 = 2
Alternatively, we can find roots of Auxiliary equation in this case which are s 1, so no
poles lie on Imaginary axis.
Remember, if and only if there is a row of complete zeroes can the roots lie on Imaginary
axis and else poles lie only in LHP and RHP. Also, existence of Auxiliary Equation does not
guarantee existence of imaginary poles as evident in previous example.
© Kreatryx. All Rights Reserved. 10 www.kreatryx.com
Control Systems (Stability)
Relative stability analysis is using Routh Array
1 1
s a2 s a1
System (2) System (1)
Both system 1 & system 2 are absolutely stable system. System 2 is relatively more stable
then system 1 because time constant of System-2 is less than System-1 so transient dies out
faster in System-2 as compared to System-1.
So, the condition for relative stability becomes that the system whose poles have more
negative real part will be more stable.
So, to judge the relative stability using Routh Criteria we shift the imaginary axis so as to
lie between the poles of two systems so that poles of one system lie on right side of
modified axis and poles of other lie to the left of axis. SO one system will be unstable with
respect to modified axis and other will be stable.
The system which is still stable will be adjudged being relatively more stable.
Solved Examples
3 2
Problem: s 7s 25s 39 0 .Check how many roots have real part more negative than -
1?
Solution: Shifting the origin s = - 1 by substituting (s = z – 1)
z 1 3 7 z 1 2 25 z 1 39 P z
P z z3 4z2 14z 20 0
© Kreatryx. All Rights Reserved. 11 www.kreatryx.com
Control Systems (Stability)
Routh array
z3 1 14
z2 4 20
z1 9
z0 20
As sign of all elements of first column of Routh Array are positive, which implies that all roots
of original characteristics equation in z – domain lie to the left of z = -0.
In s-domain, all poles will then lie to the left of s = -1.
Shortcut: Substitute the given point (eg GH = 0, put s = -1) in the poly nominal, assuming
the points makes it stable.
If LHS > 0, all roots lie in LS of s = -1
If LHS = 0, one root lie on shifted axis & rest lie on left
Put s = - 1 in above example & LHS > 0, so all poles lie to the left of line s = -1.
Note: This process involves repeatedly shifting the axis by hit and trial as we do not know
exact location of poles. So, Routh Criteria is preferable to judge Absolute Stability instead of
Relative Stability.
Application of Routh criteria to linear feedback system
Closed loop transfer function
C s K
R s
s s2 s 1 s 4 K
2
Characteristics equation is: s s s 1 s 4 K 0
s4 5s3 5s2 4s K 0
© Kreatryx. All Rights Reserved. 12 www.kreatryx.com
Control Systems (Stability)
Routh Array:
s4 1 5 K
s3 5 4
21
s2 K
5
84 21
s1 5k
5 5
s0 K
Sign of all elements in first column must be positive, the condition for stability requires that
84
K>0 & K
25
84
So range of K is 0 k
25
84
When k , the coefficient of s1 is reduced to zero and hence row preceding it becomes
25
Auxiliary Equation given by:
21 2 84 4
s 0 => s j j
5 25 5
4
Hence, frequency of self-sustained oscillations is rad s
5
This frequency is also the natural frequency of oscillations or un-damped frequency.
When system is only stable for certain range of some parameter it is called as Conditionally
Stable.
Solved Examples
Problem: Find the range of K for stability of unity feedback system whose Open Loop
Transfer Function is given below:
K
G s
s2 2s 2 s 2
Also, find natural frequency of oscillations of this system.
© Kreatryx. All Rights Reserved. 13 www.kreatryx.com
Control Systems (Stability)
Solution:
Characteristic equation of given system is :
1 G s 0
K
1 0
s2 2s 2 s 2
s3 4s2 6s 4 K 0
Routh Array:
s3 1 6
s2 4 4 K
s1
20 k
4
s0 4 K
20 K
For stability, 0 k 20 & 4 k 0 K 4
4
So range of k for stability 4 k 20
When k = 20, coefficient of s1 goes to zero, system becomes marginally stable as poles will
lie on Imaginary Axis.
Auxiliary polynomial: 4s2 4 20 0
s2 6 => s j 6 rad s
Frequency of oscillations 6 rad s
Limitations of Routh Criteria
All coefficient of characteristic equation must be real.
The sign changes in 1st column of routh array determines poles lying in RHS of s – plane
but not their locations.
Relative Stability cannot be easily determined.
© Kreatryx. All Rights Reserved. 14 www.kreatryx.com
Control Systems (Stability)
Types of Stability
Absolutely Stable: If the system is stable for all values of system parameters and response is
bounded for all bounded inputs. In such a case, the roots of characteristic equation must lie
in left half plane for all values of system parameter.
Marginally Stable: If the system has one or more pairs of simple poles lying on the
imaginary axis then response to the input is bounded if poles of Input do not coincide with
system poles else the response is unbounded.
Conditionally Stable: If the system response is stable or bounded for certain values of some
system parameter and unstable for other values, then the system is said to be conditionally
stable.
© Kreatryx. All Rights Reserved. 15 www.kreatryx.com
You might also like
- Lecture 14, 15 StabilityDocument45 pagesLecture 14, 15 StabilityHamza KhanNo ratings yet
- Lecture 14 StabilityDocument26 pagesLecture 14 StabilityHamza KhanNo ratings yet
- 2 - Module3-Routh Stability CriterionDocument15 pages2 - Module3-Routh Stability CriterionShashankaNo ratings yet
- PDC Minor 2 - SlidesDocument190 pagesPDC Minor 2 - SlidesPiyush AmbulgekarNo ratings yet
- PDC Minor 2 - SlidesDocument190 pagesPDC Minor 2 - SlidesPiyush AmbulgekarNo ratings yet
- 2 - Stability of Linear Control SystemsDocument34 pages2 - Stability of Linear Control SystemsHassan El SayedNo ratings yet
- Lect 10 Stability AnalysisDocument7 pagesLect 10 Stability AnalysisZaidoon MohsinNo ratings yet
- Stability: Dr. Issam ELGMATIDocument27 pagesStability: Dr. Issam ELGMATI7moud alajlaniNo ratings yet
- Transient & Steady State Response AnalysisDocument32 pagesTransient & Steady State Response AnalysisMisbah Sajid ChaudhryNo ratings yet
- Stability R-H, Root Locus, Time Domain SpecsDocument81 pagesStability R-H, Root Locus, Time Domain SpecsTarek A-RNo ratings yet
- Week 6 - Stability of Linear Control Systems - PDFDocument45 pagesWeek 6 - Stability of Linear Control Systems - PDFgigoNo ratings yet
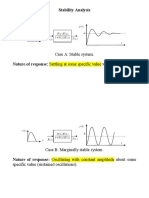
- Stability Analysis: Case A: Stable SystemDocument31 pagesStability Analysis: Case A: Stable SystemLakshay KhichiNo ratings yet
- PDC Lecture Notes 7 - Stability of Closed-Loop Systems 2018Document56 pagesPDC Lecture Notes 7 - Stability of Closed-Loop Systems 2018R-A PascualNo ratings yet
- SE302: Linear Control Systems: StabilityDocument30 pagesSE302: Linear Control Systems: StabilityyfmihweasaNo ratings yet
- CS Time Response TDocument26 pagesCS Time Response TPrasun SinghalNo ratings yet
- Block Diagrams and The Stability of Linear Feedback SystemsDocument26 pagesBlock Diagrams and The Stability of Linear Feedback Systemshasan bishNo ratings yet
- ECNG-4010 Lecture 09Document28 pagesECNG-4010 Lecture 09Abel BatuNo ratings yet
- 117920Document20 pages117920saravanan.9344308178No ratings yet
- Module 4Document49 pagesModule 4VARUN B MNo ratings yet
- D - Stability AnalysisDocument5 pagesD - Stability AnalysisAnanthan SrijithNo ratings yet
- System StabilityDocument16 pagesSystem Stabilityeugeni madaNo ratings yet
- Routh CriteriaDocument17 pagesRouth CriteriaTyson LawrenceNo ratings yet
- Concepts of Stability and Algebraic Criteria: by Nand KishoreDocument17 pagesConcepts of Stability and Algebraic Criteria: by Nand KishoreTyson LawrenceNo ratings yet
- Lecture 7 & 8 (Stability Analysis)Document35 pagesLecture 7 & 8 (Stability Analysis)muhammad hamzaNo ratings yet
- CS Design 01Document13 pagesCS Design 01Prasun SinghalNo ratings yet
- Chapter 11 Chang.2Document39 pagesChapter 11 Chang.2satya sagarNo ratings yet
- Stability Analysis-Control SystemDocument29 pagesStability Analysis-Control SystemNanmaran RajendiranNo ratings yet
- Stability of Control Systems - GATE Study Material in PDFDocument6 pagesStability of Control Systems - GATE Study Material in PDFShrishanti KaleNo ratings yet
- Block Diagram and StabilityDocument101 pagesBlock Diagram and Stabilityhasan bishNo ratings yet
- Assignment 04: 1 What Is Meant by Stability of A Control System? Explain Routh Stability CriteriaDocument4 pagesAssignment 04: 1 What Is Meant by Stability of A Control System? Explain Routh Stability CriteriaSyed AfzalNo ratings yet
- Control: Hooman SamaniDocument43 pagesControl: Hooman SamaniGonzales PhanieNo ratings yet
- Lecture 10: Stability and Nonlinear Systems: Department of Chemical Engineering I.I.T. Bombay, IndiaDocument10 pagesLecture 10: Stability and Nonlinear Systems: Department of Chemical Engineering I.I.T. Bombay, IndiaLikhithNo ratings yet
- Unit 4 Stability AnalysisDocument28 pagesUnit 4 Stability AnalysisrocklinetoNo ratings yet
- Module 5 - L3: Routh Stability CriterionDocument19 pagesModule 5 - L3: Routh Stability CriterionAngelus Vincent GuilalasNo ratings yet
- Control Chapter 1 - Lecture 1Document29 pagesControl Chapter 1 - Lecture 13re0oooNo ratings yet
- Feedback AmpDocument76 pagesFeedback AmpBayu AjiNo ratings yet
- Chapter 5Document78 pagesChapter 5hailegebreselassie24No ratings yet
- Stability of Linear Control System: Bounded-Input Bounded-Output (BIBO) StabilityDocument9 pagesStability of Linear Control System: Bounded-Input Bounded-Output (BIBO) StabilityFida HussainNo ratings yet
- CH 3Document91 pagesCH 3wehabekodaNo ratings yet
- Stability of Linear Control System: Bounded-Input Bounded-Output (BIBO) StabilityDocument9 pagesStability of Linear Control System: Bounded-Input Bounded-Output (BIBO) Stabilitymeseret sisayNo ratings yet
- Ee9118 Dynamics & Control Stability AnalysisDocument30 pagesEe9118 Dynamics & Control Stability AnalysisAna ZanaNo ratings yet
- Unit 4 Stability AnalysisDocument28 pagesUnit 4 Stability AnalysisrocklinetoNo ratings yet
- Stability Analysis For Control SystemsDocument36 pagesStability Analysis For Control SystemsSARTHAK BAPATNo ratings yet
- 505 - Lec 11 PDFDocument28 pages505 - Lec 11 PDFUdara DissanayakeNo ratings yet
- EMS507 Lecture 3 - System StabilityDocument21 pagesEMS507 Lecture 3 - System Stability124ll124No ratings yet
- 05 Time Response AnalysisDocument41 pages05 Time Response AnalysisFadly ShafiqNo ratings yet
- Transient and Steady State Response Analysis: Module - 3Document22 pagesTransient and Steady State Response Analysis: Module - 3Rajath UpadhyaNo ratings yet
- Control Systems U3 (TEL306)Document84 pagesControl Systems U3 (TEL306)Ruvenderan SuburamaniamNo ratings yet
- Advanced Control Systems (ACS) : Transfer Function and Stability of LTI SystemsDocument22 pagesAdvanced Control Systems (ACS) : Transfer Function and Stability of LTI SystemsFahmeed Ali MeoNo ratings yet
- Chapter 6 - Steady-State AnalysisDocument32 pagesChapter 6 - Steady-State AnalysisANDREW LEONG CHUN TATT STUDENTNo ratings yet
- System Stability: Chapter Objective: - System Stability - Routh-Hurwitz's Stability CriterionDocument23 pagesSystem Stability: Chapter Objective: - System Stability - Routh-Hurwitz's Stability CriterionUn Yong KimNo ratings yet
- Chapter 6Document20 pagesChapter 6Duncan KingNo ratings yet
- Module - 5 - Control SystemDocument16 pagesModule - 5 - Control SystemRonitNo ratings yet
- Routh-Hurwtz Criterion & Root-Locus Criteria: Stability of Feedback Control SystemsDocument19 pagesRouth-Hurwtz Criterion & Root-Locus Criteria: Stability of Feedback Control Systemsember_memoriesNo ratings yet
- 1437235816control Systems (K-Wiki Root Locus) PDFDocument24 pages1437235816control Systems (K-Wiki Root Locus) PDFRitarshiChakrabortyNo ratings yet
- Chapter 6 - The Stability of Linear Feedback PDFDocument71 pagesChapter 6 - The Stability of Linear Feedback PDFHei Kan ChengNo ratings yet
- StabilityDocument20 pagesStabilityravalNo ratings yet
- KIG 4001 Control Engineering (Group 4) : Time Response AnalysisDocument29 pagesKIG 4001 Control Engineering (Group 4) : Time Response AnalysisNurul Iman Nur ElahiNo ratings yet
- Combinational Logic Circuits MaterialDocument27 pagesCombinational Logic Circuits MaterialananthmuthNo ratings yet
- Transfer Function 2Document37 pagesTransfer Function 2Ruben Kandulna100% (1)
- Digital Electronics (K-Wiki - Boolean Algebra)Document33 pagesDigital Electronics (K-Wiki - Boolean Algebra)SUNOBHAINo ratings yet
- Logic FamiliesDocument16 pagesLogic FamiliesPrasun SinghalNo ratings yet
- CS Design 01Document13 pagesCS Design 01Prasun SinghalNo ratings yet
- Transfer Function 1Document24 pagesTransfer Function 1Ruben KandulnaNo ratings yet
- Locking Table Practice S5 Locking Table Practice Locking Table PracticeDocument34 pagesLocking Table Practice S5 Locking Table Practice Locking Table PracticePrasun Singhal100% (1)
- S4 - Mechanical Signalling - Double Wire PDFDocument105 pagesS4 - Mechanical Signalling - Double Wire PDFPooja SinghNo ratings yet
- S9Document171 pagesS9Prasun SinghalNo ratings yet
- S8 SodDocument215 pagesS8 SodAvinash Kumar SinghNo ratings yet
- S2Document100 pagesS2Prasun SinghalNo ratings yet
- S7Document88 pagesS7Prasun SinghalNo ratings yet
- Neral Principle of Design (VMP) PDFDocument210 pagesNeral Principle of Design (VMP) PDFPrasun SinghalNo ratings yet
- 1.chapter-1 - Electric Circuits and Fields (VMP) PDFDocument88 pages1.chapter-1 - Electric Circuits and Fields (VMP) PDFPrasun SinghalNo ratings yet
- Neral Principle of Design (VMP) PDFDocument210 pagesNeral Principle of Design (VMP) PDFPrasun SinghalNo ratings yet
- VipassanaDocument6 pagesVipassanaPrasun SinghalNo ratings yet
- J Kabat-Zinn - Guided Mindfulness Meditation 1 Booklet PDFDocument10 pagesJ Kabat-Zinn - Guided Mindfulness Meditation 1 Booklet PDFEngidrems50% (2)
- Air Circuit Breaker CataloguesDocument37 pagesAir Circuit Breaker CataloguesPrasun Singhal0% (1)
- 1.chapter-1 - Electric Circuits and Fields (VMP) PDFDocument88 pages1.chapter-1 - Electric Circuits and Fields (VMP) PDFPrasun SinghalNo ratings yet
- Mathematics 2Document24 pagesMathematics 2MAX PAYNENo ratings yet
- Gate Gate Gate GA: Electronic Devices and CircuitsDocument4 pagesGate Gate Gate GA: Electronic Devices and CircuitsNagarjun RamNo ratings yet
- Chapter 11 Number TheoryDocument32 pagesChapter 11 Number TheoryRodel PelimianoNo ratings yet
- Introductory Methods of Numerical Analysis: Fifth EditionDocument11 pagesIntroductory Methods of Numerical Analysis: Fifth EditionAlokPatelNo ratings yet
- Properties of The Trinomial DistributionDocument2 pagesProperties of The Trinomial DistributionPerry01No ratings yet
- Geometric Sequences and Series Wk-2 MSDocument12 pagesGeometric Sequences and Series Wk-2 MSmanvithNo ratings yet
- 2B. Complex Numbers L-ViDocument37 pages2B. Complex Numbers L-ViShashwat PalNo ratings yet
- SOUTH AFRICAN MATHEMATICS TEAM COMPETITION: 2015 JuniorDocument2 pagesSOUTH AFRICAN MATHEMATICS TEAM COMPETITION: 2015 Juniorพงศ์ทอง แซ่เฮ้งNo ratings yet
- Improved Modal Truncation Approximant: A Hybrid ApproachDocument8 pagesImproved Modal Truncation Approximant: A Hybrid Approachrobert brownNo ratings yet
- System Dynamics Bookmarked PDFDocument535 pagesSystem Dynamics Bookmarked PDFjdsjfbNo ratings yet
- Algebra1 - Glencoe - Lessons 7-3 Rational - Exponents - Pages47Document47 pagesAlgebra1 - Glencoe - Lessons 7-3 Rational - Exponents - Pages47Karen GeorgeNo ratings yet
- BSI Complex Variables Cloplos, Fall 2020Document5 pagesBSI Complex Variables Cloplos, Fall 2020Ahmar KhanNo ratings yet
- MATLAB Code For Structural Analysis of 2-D Structures Subjected To Static and Self-Weight Loading ConditionsDocument9 pagesMATLAB Code For Structural Analysis of 2-D Structures Subjected To Static and Self-Weight Loading ConditionsAnax SouzaNo ratings yet
- Stage 1 Math Methods A Exam Guide 2020Document6 pagesStage 1 Math Methods A Exam Guide 2020Maan PatelNo ratings yet
- Lesson PlanDocument3 pagesLesson Planapi-248632074100% (2)
- Curvature and Radius of CurvatureDocument1 pageCurvature and Radius of CurvatureMad MaxNo ratings yet
- Math 201 Final TestDocument1 pageMath 201 Final TestMichael GbonehNo ratings yet
- Acoustics Homework 3 SolutionDocument6 pagesAcoustics Homework 3 SolutionAnshul GoyalNo ratings yet
- Homework For Module 3 Part 2Document6 pagesHomework For Module 3 Part 2bita younesian100% (3)
- FORTRANDocument58 pagesFORTRANAkshay SharmaNo ratings yet
- Cosine, Sine and Tangent of Multiple Angles (Recursive Formula)Document5 pagesCosine, Sine and Tangent of Multiple Angles (Recursive Formula)Toyen BlakeNo ratings yet
- Fib FormulaeDocument23 pagesFib FormulaeAnonymous L4GY7kqNo ratings yet
- Ramirez-Riberos Et AlDocument15 pagesRamirez-Riberos Et AlcelticpenguinNo ratings yet
- 17mat41 PDFDocument3 pages17mat41 PDFBroNo ratings yet
- Pre-Calculus: Quarter 1 - Module 7Document20 pagesPre-Calculus: Quarter 1 - Module 7keith tambaNo ratings yet
- 1.5 Inverse of A Relation Notes and PracticeDocument16 pages1.5 Inverse of A Relation Notes and PracticeMath 30-1 EDGE Study Guide Workbook - by RTD LearningNo ratings yet
- Tutorial Sheet 1Document3 pagesTutorial Sheet 1Chirag KadamNo ratings yet
- 2EC6303-Signals and Systems QBDocument10 pages2EC6303-Signals and Systems QBShyla RajNo ratings yet
- 1 Solution PDFDocument6 pages1 Solution PDFTooba MukhtarNo ratings yet
- Fluid NotesDocument11 pagesFluid NotesDeeptanshu ShuklaNo ratings yet
- Math Wizard 2020Document7 pagesMath Wizard 2020Cedrixe MadridNo ratings yet
- Methods of IntegrationDocument39 pagesMethods of IntegrationAyush RajputNo ratings yet