On the other hand, rejection of the null hypothesis implies stationary, hence

the remaining 27 variables are identified as stationary processes I(0). Since it is

possible for non-stationary variables to have orders of integration higher than one,

and because the ADF tests consider only one unit root, the resulting non-stationary

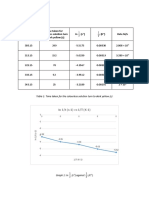
variables need to be re-tested in first-differences. Accordingly, Table 4-2 presents the

results of a second unit root test only on the 31 non-stationary variables detected at

α=0.10 in first run of the test. These tests are for series in log first differences.

Variables for which the null hypothesis of non-stationarity is rejected are profiled as

I(1), that is they only need to be differenced once in order to achieve stationarity.

Table 4-2. Stationary Tests (Unit Root) in Log First Differences

Total Stochastic Trends in Log First
Test
Series Differences
0.10* % 0.05* % 0.01* %
Augmented Dickey-Fuller 31 0 0 0 0 0 0
ERS^ 46 13 28.3 13 28.3 22 47.83
KPSS† 39 8 20.5 5 12.8 0 0
Ng and Perron -DFGLS 53 24 45.3 28 52.8 32 60.38
Ng and Perron -MPT 49 31 63.3 32 65.3 37 75.51
Ng and Perron -MSB 51 31 60.8 34 66.7 38 74.51
Ng and Perron -MZ 49 31 63.3 32 65.3 37 75.51
Ng and Perron -MZalpha 50 31 62 33 66 38 76
Ng and Perron -PT 49 30 61.2 32 65.3 37 75.51
Phillips-Perron 25 0 0 0 0 0 0
Total 442 199 45 209 47.3 241 54.52
^ Elliott-Rothenberg-Stock, †Kwiatkowski-Phillips-Schmidt-Shin, *Significance level (α).

On the other hand, variables for which the null hypothesis could not be

rejected, need to pass once again through a third set of unit root tests, this time in log

second-differences as shown in Table 4-3. In the same fashion higher orders of

integration I(2), and I(3) are identified. It is evident that variables present a mix of

orders of integration, some are I(0), others I(1), and I(2), and even I(3). And as

60