1

Introduction to Digital
Modulation
Instructor: M.A. Ingram
ECE4823
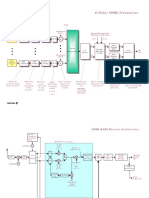
Digital Communication
Transmitter
User
Interface
Encoder Modulator
RF
Front
End
antenna
bits
0110
more bits
011001
waveforms
(symbols)
Frequency
up-conversion
and amplification
A simplified block diagram:
interleaver
Digital Communications
Receiver
A simplified block diagram:
User
Interface
Decoder Demodulator
RF
Front
End
antenna
bits
0110
soft detections
of coded bits
011001
waveforms
(faded symbols
plus noise)
Low-noise amplification
and frequency
down-conversion
deinterleaver
Symbols
In each symbol period, T
s
, a digital
modulator maps N coded bits word to a
transmitted waveform from a set of
M=2
N
possible waveforms
Each waveform corresponds to an
information symbol, x
n
For Binary symbols, N=1
Detection
The job of the receiver is to determine
which symbols were sent and to
reconstruct the bit stream that created
them
Definitions
Bit Rate (bits per sec or bps)
Bandwidth Efficiency (bps/Hz)
where B is the bandwidth occupied by
the signal
S
T N R / =
B R
B
/ =
2
Shannon Theorem
In a non-fading channel, the maximum
bandwidth efficiency, or Shannon
Capacity is
SNR = signal-to-noise ratio
( ) SNR
MAX
B
+ = 1 log
2

Pulses
A symbol period, T
s
, suggests a
localization in time
Localization in frequency is also
necessary to enable frequency division
multiplexing
Regulatory agencies provide spectral
masks to limit the distribution of power
in the frequency domain
Example: Linear Modulation
s(t) is the output of the modulator
g(t) is the complex envelope
p(t) is the basic pulse
x
n
is the nth symbol
A is the amplification in the transmitter
{ }
) ( ) (
) ( Re ) (
2
S
n
n
t f j
nT t p x A t g
e t g t s
c
=
=

Rectangular Pulses
Suppose p(t) is a rectangular pulse
This pulse is not used in practice, but is OK
for illustration
S
T 0
t
S
T
2
) (t p
Binary Phase Shift Keying
(BPSK)
For BPSK, each symbol carries one bit
of information { } 1 , 1
n
x
0
S
T
t
S
T
A
2
) (t g
L
S
T 2
S
T
A
2

1 1 1 1 0 0 0
BPSK-Modulated Carrier
The information is in the phase of the
carrier
t
S
T
A
2
) (t s
L
S
T
A
2

1 1 1 1 0 0 0
3
Power Spectral Density (PSD)
of Linear Modulation
Assume that the symbol sequence {x
n
} is iid
and zero mean. Then, the PSD of s(t) is
where
and is the Fourier Transform of
| | ) ( ) (
2
1
) (
c g c g s
f f S f f S f S + =
{ }
2
2
2
) (
2
) ( f P
T
x E A
f S
S
n
g
=
) ( f P ) (t p
Bandwidth Properties
The RF bandwidth of the modulated
carrier is two times the baseband
bandwidth of
which is clearly seen to depend on the
bandwidth of the pulse
{ }
2
2
2
) (
2
) ( f P
T
x E A
f S
S
n
g
=
Fourier Transform of the
Rectangular Pulse
( ) ( )
( ) ( )
( )
( ) ( ) ( )
S S S S
S
S
S
S
T
S
T
S
fT T fT j fT
T f
fT j
f j
fT j
T f j
ft j
T
dt ft j
T
dt ft j t p f P
S
S
sinc 2 exp sin
2 exp
2
1 2 exp 2
2
2 exp 2
2 exp
2
2 exp ) ( ) (
0
0

=
= =

+

PSD for BPSK and the
Rectangular Pulse

|x
n
|
2
=1
| | ( ) | | ( ) | |
S c S c s
T f f T f f
A
f S + =
2 2
2
sinc sinc
2
) (
( )
S S
fT T f P
2
2
sinc 2 ) ( =
{ }
( )
S
S
n
g
fT A
f P
T
x E A
f S
2 2
2
2
2
sinc
) (
2
) (
=
=
) ( f S
s
c
f
c
f
Received Signal
The received signal has been attenuated by path loss
and multipath fading and has added noise
t
S
T
A t a
2
) (
L
1 1 1 1 0 0 0
Channel
Gain
) ( ) 2 cos( ) ( ) ( ) ( t n t f nT t p x A t a t r
c c S
n
n
+ + =


BPSK Demodulator
The output of the correlator is a sequence of
noisy versions of the transmitted symbol
sequence
r(t)
( ) t f
T t Aa
c
S
2 cos
2
) (
1
( )
( )
dt
S
S
nT
T n

1
demodulated
received symbols
Automatic Gain Control
.95,-1.03,-1.02,.93,-.85,.81,.74
To deinterleaver and decoder
4
Integrate and Dump Output
Consider one symbol period and the
rectangular pulse:
v
n
is a zero-mean Gaussian RV with variance
( ) ( ) ( )
( )
n b n c
S
b
S
n
c
S
c
S
b
n c
S
v x dt t f t n
T
dt
T
x
dt t f
T
t n t f
T
x dt t f
T
t r R
+ = + =
|
|
.
|

\
|
+ = =

S S
S S
T
0
T
0
T
0
T
0
2 cos ) (
2
1
2 cos
2
) ( 2 cos
2
2 cos
2
) (
2
0 2
N
v
=
channel gains and TX
power lumped into
b

Conditional PDFs
Recall
b

b

( )
(
(
(
(

|
.
|

\
|
+

|
.
|

\
|
=
=
2
2
exp
2
2
1
) (
0
2
0
1 |
N
r
N
r f
b
x R n

( )
(
(
(
(

|
.
|

\
|

|
.
|

\
|
=
=
2
2
exp
2
2
1
) (
0
2
0
1 |
N
r
N
r f
b
x R n

n b n
v x R + =
r
Conditional Probability of Bit
Error
If x
n
is -1, then an error happens if R>0
b

+
=
= =
= > = =
0
1 |
) 1 | (
) 1 | 0 ( ) 1 | (
dr x r f
x R P x error P
n x R
n n
n
) 1 | (
1 |
=
= n x R
x r f
n
r
Conditional Probability of Error
Expression
( )
|
|
.
|

\
|
=
|
|
|
|
.
|

\
|

= =

+
=
0 0 0
1 |
2
2
0
) 1 | (
N
Q
N
Q dr x r f
b b
n x R
n

Same for other kind of error, by symmetry
Unconditional Probability of Bit
Error
Assume the two possible values of x
n
are equally likely
|
|
.
|

\
|
=
= + = =
0
2
) 1 | (
2
1
) 1 | (
2
1
) (
N
Q
x error P x error P error P
b
n n

How to Improve System

Performance
Increase symbol energy
Decrease average noise power
|
|
.
|

\
|
=
0
2
) (
N
Q error P
b

2 /
0
N
5
References
[Rapp, 02] T.S. Rappaport, Wireless
Communications, Prentice Hall, 2002
[Stuber, 01] Gordon Stuber, Principles
of Mobile Communication, 2
nd
ed,
Kluwer Academic Publishers, 2001.