Professional Documents
Culture Documents
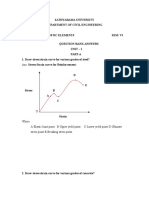
Reinforced Concrete Beams
Reinforced Concrete Beams
Uploaded by
Joseph PayatCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Reinforced Concrete Beams
Reinforced Concrete Beams
Uploaded by
Joseph PayatCopyright:
Available Formats
CIVL 1112
Strength of Reinforced Concrete Beams
Reinforced Concrete Beams
Reinforced Concrete Beams
Mathematical modeling of reinforced concrete is essential to
civil engineering
Mathematical modeling of reinforced concrete is essential to
civil engineering
Concrete as a material
Concrete in a structure
Stress distribution in a reinforced concrete beam
Reinforced Concrete Beams
Reinforced Concrete Beams
Mathematical modeling of reinforced concrete is essential to
civil engineering
Mathematical modeling of reinforced concrete is essential to
civil engineering
Blast failure of a reinforced concrete wall
Geometric model a reinforced concrete bridge
Reinforced Concrete Beams
Mathematical modeling of reinforced concrete is essential to
civil engineering
Blast failure of a reinforced concrete wall
Reinforced Concrete Beams
Mathematical model for failure in an unreinforced concrete
beam
1/11
CIVL 1112
Strength of Reinforced Concrete Beams
Reinforced Concrete Beams
2/11
Reinforced Concrete Beams
Mathematical model for failure in an reinforced concrete beam
In the reinforced concrete beam project, there are three
different failure mode we need to investigate
Reinforced Concrete Beams
Reinforced Concrete Beams
First, lets consider the loading of the beam
The purpose of RC is the reinforcement of areas in concrete
that are weak in tension
P/2
P/2
P/2
Reinforced Concrete Beams
P/2
Reinforced Concrete Beams
Lets look at the internal forces acting on the beam and
locate the tension zones
The shear between the applied load and the support is
constant V = P/2
P
P
F 2 V
P/2
V is the shear force
P/2
P
2
F 2 V
P/2
V
P/2
P
2
CIVL 1112
Strength of Reinforced Concrete Beams
Reinforced Concrete Beams
The shear between the applied load and the support is
constant V = P/2
3/11
Reinforced Concrete Beams
The shear between the applied load and the support is
constant V = P/2
The shear force V = P/2 is constant between the applied load
and the support
P/2
P/2
P/2
P/2
Reinforced Concrete Beams
Reinforced Concrete Beams
Lets look at the internal moment at section between the
supports and applied load
Lets look at the internal moment at section between the
supports and applied load
M 2 x
The bending moment is the internal reaction to forces which
cause a beam to bend.
X max = 8 in.
M is the bending moment
P/2
M P/2
4P
P/2
Bending moment can also be referred to as torque
(lb.-in.)
Reinforced Concrete Beams
The top of the beam is in compression and the bottom of the
beam is in tension
Reinforced Concrete Beams
To model the behavior of a reinforced concrete beam we will
need to understand three distinct regions in the beam.
Two are illustrated below; the third is called shear.
Compression force on the upper
Bending
distributed
part ofmoment
the concrete
beamon
the cut surface
Bending moment distributed on
surface
Compression
MCthe cut
MC
P
2
Tension force on the lower
part of the concrete beam
P
2
Tension
CIVL 1112
Strength of Reinforced Concrete Beams
Reinforced Concrete Beams
We need models to help us with compression, tension, and
shear failures in concrete
4/11
Reinforced Concrete Beams
We need models to help us with compression, tension, and
shear failures in concrete
Compression
Tension
Reinforced Concrete Beams
We need models to help us with compression, tension, and
shear failures in concrete
Reinforced Concrete Beams
We need models to help us with compression,
tension, and shear failures in concrete
Shear
Shear
Shear
Compression
Shear
Tension
Reinforced Concrete Beams
Reinforced Concrete Beams
Compression and tension failures in a reinforced
concrete beam
Compression and tension failures in a reinforced
concrete beam
CIVL 1112
Strength of Reinforced Concrete Beams
Reinforced Concrete Beams
Shear failure in a reinforced concrete beam
Reinforced Concrete Beams
Lets focus on how to model the ultimate tensile load in a
reinforced concrete beam
Reinforced Concrete Beams
Shear failure in a reinforced concrete beam
Reinforced Concrete Beams
Typical rebar configuration to handle tension and
shear loads
Tension
Reinforced Concrete Beams
Reinforced Concrete Beams
Typical rebar configuration to handle tension and
shear loads
Typical rebar configuration to handle tension and
shear loads
5/11
CIVL 1112
Strength of Reinforced Concrete Beams
Whitney Rectangular Stress Distribution
6/11
Whitney Rectangular Stress Distribution
In the 1930s, Whitney proposed the use of a rectangular
compressive stress distribution
In the 1930s, Whitney proposed the use of a rectangular
compressive stress distribution
k3fc
0.85fc
k 2x
0.5a
As
T
Whitney Rectangular Stress Distribution
Whitney Rectangular Stress Distribution
Assume that the concrete contributes nothing to the tensile
strength of the beam
k3fc
0.85fc
k 2x
Assume that the complex distribution of compressive
stress in the concrete can be approximated by a rectangle
0.5a
As
T
Whitney Rectangular Stress Distribution
0.85fc
Whitney Rectangular Stress Distribution
The height of the stress box, a, is defined as a percentage
of the depth to the neural axis
a 1c
c
h
As
0.85fc
k 2x
k3fc
0.5a
The height of the stress box, a, is defined as a percentage
of the depth to the neural axis
f 'c 4000 psi
1 0.85
0.85fc
0.5a
f 'c 4000 psi
0.5a
f 'c 4000
0.65
1000
1 0.85 0.05
T
CIVL 1112
Strength of Reinforced Concrete Beams
Whitney Rectangular Stress Distribution
Whitney Rectangular Stress Distribution
The values of the tension and compression forces are:
If the tension force capacity of the steel is too high, than
the value of a is large
C 0.85f 'c ba
T As fy
0.85fc
F 0 T C
a
7/11
0.5a
0.85fc
As fy
0.85f 'c b
0.5a
a
d
If a > d, then you have too much steel
As fy
0.85f 'c b
Whitney Rectangular Stress Distribution
Whitney Rectangular Stress Distribution
The internal moment is the value of either the tension or
compression force multiplied the distance between them.
If the tension force capacity of the steel is too high, than
the value of a is large
M T d 2
a
M As fy d
2
0.85fc
0.5a
0.85fc
Substitute the value for a
Whitney Rectangular Stress Distribution
Reinforced Concrete Beams
Lets focus on how to model the ultimate shear load in a
reinforced concrete beam
We know that the moment in our reinforced
concrete beans is
M 4P
Ptension
M 4P
Af
M As fy d 0.59 s y
f
'c b
Af
Af
= s y d - 0.59 s y
4
f'c b
0.5a
Af
M As fy d 0.59 s y
f 'c b
The internal moment is the value of either the tension or
compression force multiplied the distance between them
M As fy d
2
Shear
Shear
CIVL 1112
Strength of Reinforced Concrete Beams
Reinforced Concrete Beams
We can approximate the shear failure in unreinforced concrete
as:
8/11
Reinforced Concrete Beams
Lets consider shear failure in reinforced concrete
Vc 2 f 'c bd
If we include some reinforcing for shear the total shear
capacity of a reinforce concrete bean would be approximated
as:
Vn Vc Vs
Vs
Av fy d
Vn
P
2
Af d
Pshear 2 v y 2 f 'c bd
s
Reinforced Concrete Beams
Reinforced Concrete Beams
Lets focus on how to model the ultimate compression load in
a reinforced concrete beam
There is a balanced condition where the stress in the steel
reinforcement and the stress in the concrete are both at their
yield points
The amount of steel required to reach the balanced strain
condition is defined in terms of the reinforcement ratio:
Compression
Reinforced Concrete Beams
The limits of the reinforcement ratio are established
as:
Reinforcement ratio definition
A
s
bd
Reinforced Concrete Beams
The limits of the reinforcement ratio are established
as:
c
0.600
d
as function of c/d
c f 'c
d fy
As
bd
Compression
0.375
0.85 1
Beam failure is controlled by
compression
c
0.600 Transition between tension
d
and compression control
c
0.375
d
Beam failure is controlled by
tension
CIVL 1112
Strength of Reinforced Concrete Beams
9/11
Reinforced Concrete Beams
Reinforced Concrete Beams
Lets consider compression failure in over reinforced concrete.
First, let define an equation that given the stress in the tensile
steel when concrete reaches its ultimate strain.
Lets consider compression failure in over reinforced concrete
First, let define an equation that given the stress in the tensile
steel when concrete reaches its ultimate strain
d c
fsteel 87,000 psi
c
If fsteel
M 4P
only if fs f y
c
< fy then or
0.600
d
Pcompression
a
d c
Mcompression As
d 2 87,000 psi
c
Reinforced Concrete Beams
Consider the different types of failures in reinforced concrete:
As d c
a
d 87,000 psi
4 c
2
Reinforced Concrete Beam Analysis
Lets use the failure models to predict the ultimate strength-toweight (SWR) of one of our reinforced concrete beams from
lab
Consider a beam with the following characteristics:
Concrete strength fc = 5,000 psi
Steel strength fy = 60,000 psi
The tension reinforcement will be 2 #4 rebars
The shear reinforcement will be #3 rebars bent in a U-shape spaced at
4 inches.
Use the minimum width to accommodate the reinforcement
Reinforced Concrete Beam Analysis
Reinforcing bars are denoted by the bar number. The
diameter and area of standard rebars are shown below.
Reinforced Concrete Beam Analysis
Based on the choice of reinforcement we can compute an
estimate of b and d
#4 rebar diameter
Bar #
3
4
5
6
7
8
9
10
11
2
Diameter (in.) As (in. )
0.375
0.11
0.500
0.20
0.625
0.31
0.750
0.44
0.875
0.60
1.000
0.79
1.128
1.00
1.270
1.27
1.410
1.56
Minimum cover
b 2 0.5 in 2(0.75 in ) 2(0.375 in )
0.75 in
d
6 in.
#4
#3 rebar diameter
Space between bars
4.0in.
CIVL 1112
Strength of Reinforced Concrete Beams
Reinforced Concrete Beam Analysis
If we allow a minimum cover under the rebars were can
estimate d
Half of #4 bar
diameter
d 6
#4
Reinforced Concrete Beam Analysis
We now have values for b, d, and As
Minimum cover
Af
M As fy d 0.59 s y
f 'c b
0.5
0.75 0.375
2
#3 rebar diameter
6 in.
4.625 in.
The As for two #4 rebars is:
6 in.
As 2(0.20 in.2 ) 0.40 in.2
#4
Reinforced Concrete Beam Analysis
10/11
Reinforced Concrete Beam Analysis
b
Compute the moment capacity
Lets check the shear model
Af d
Pshear 2 v y 2 f 'c bd
s
Af
M As fy d 0.59 s y
f 'c b
6 in.
#4
Area of two #3 rebars
0.4in.2 (60ksi)
0.4in.2 (60ksi) 4.625in. 0.59
5ksi (4in.)
2 0.11in.2 60,000psi 4.625in.
2
2 5,000psi 4in. 4.625in.
4in.
Shear reinforcement spacing
94.0 k in.
M
4
23.5 kips
35,757lb.
35.76kips
Since Ptension < Pshear therefore Ptension controls
Reinforced Concrete Beam Analysis
An 1 estimate is given as:
Lets check the reinforcement ratio
A
s
bd
Reinforced Concrete Beam Analysis
Reinforcement ratio definition
as function of c/d
c f 'c
0.85 1
d fy
To compute , first we need to estimate 1
f 'c 4000 psi
1 0.85
f 'c 4000 psi
f 'c 4000
0.65
1000
1 0.85 0.05
5,000 4,000
0.80
1,000
1 0.85 0.05
CIVL 1112
Strength of Reinforced Concrete Beams
11/11
Reinforced Concrete Beam Analysis
Reinforced Concrete Beam Analysis
Check the reinforcement ratio for the maximum steel allowed
for tension controlled behavior or c/d = 0.375
However, the maximum about of steel where compression is
in control is c/d = 0.600
0.85 1
c f 'c
5ksi
0.85(0.80)0.375
d fy
60ksi
0.021
0.85 1
0.034
c/d = 0.375 for tension
controlled behavior
As
0.4 in.2
0.022
bd 4in.(4.625in.)
The amount of steel in this beam is just a bit over the
allowable for tension controlled behavior.
Size of concrete beam
As
0.4 in.2
0.022
bd 4in.(4.625in.)
Reinforced Concrete Beam Analysis
In summary, this reinforced concrete beam will fail in tension
Unit weight of concrete
Unit weight of steel
4.625 in.
6 in.
(0.4in. )(30in.) 490lb. 145lb.
1728 in.3 ft.3
ft.3
60.42lb. 2.39lb. 62.81lb.
Reinforced Concrete Beam Analysis
Questions?
S P 23.5 kips
W 62.81 lb.
4 in.
(4in.)(6in.)(30in.) 145lb.
1728in.3 ft.3 ft.3
Additional weight of rebars
c/d = 0.600 for compression
controlled behavior
Therefore, the beam is in the lower part of the transition zone
and for our purposes is OK.
Reinforced Concrete Beam Analysis
An estimate of the weight of the beam can be made as:
c f 'c
5ksi
0.85(0.80)0.600
d fy
60ksi
#4
SWR
23,500 lb.
62.81 lb.
374.2
You might also like
- PCA Teoria-Rectangular Concrete TanksDocument27 pagesPCA Teoria-Rectangular Concrete TanksAlberto Muñoz Vizcarra100% (3)
- Concrete Anchor Bolt Design CalculationDocument10 pagesConcrete Anchor Bolt Design Calculationraghu_mn100% (5)
- ACI 318M-11 Training by Prof. David Darwin PDFDocument371 pagesACI 318M-11 Training by Prof. David Darwin PDFwisnusantari100% (1)
- The Strength of Filler Joist Floors.Document4 pagesThe Strength of Filler Joist Floors.stan80100% (1)
- 32 Samss 002 PDFDocument35 pages32 Samss 002 PDFSahilNo ratings yet
- Transmission Line Design Structures & Foundations TADP 549: Concrete Poles Design & Manufacturing Presentation 5.2Document37 pagesTransmission Line Design Structures & Foundations TADP 549: Concrete Poles Design & Manufacturing Presentation 5.2HongVuthyNo ratings yet
- Prestressed Concrete Storage TanksDocument12 pagesPrestressed Concrete Storage Tanksthorkhan42No ratings yet
- Rectangular Reinforced Concrete BeamDocument60 pagesRectangular Reinforced Concrete BeamMedianna Novita100% (1)
- RCD 01 IntroductionDocument9 pagesRCD 01 IntroductionJescel AraracapNo ratings yet
- Design Example of Reinforce Concrete BeamsDocument60 pagesDesign Example of Reinforce Concrete BeamsMario FrankistaNo ratings yet
- RCC 2 MarksDocument27 pagesRCC 2 MarksWilliam WhaiteNo ratings yet
- Shear and Diagonal Tension in Beams 4-1 4-3 20121022Document48 pagesShear and Diagonal Tension in Beams 4-1 4-3 20121022KinWaiLeongNo ratings yet
- Lecture 5Document60 pagesLecture 5Cecille Grace ReyesNo ratings yet
- 1.054/1.541 Mechanics and Design of Concrete Structures (3-0-9) Outline 9 Beam Column JointsDocument9 pages1.054/1.541 Mechanics and Design of Concrete Structures (3-0-9) Outline 9 Beam Column JointsRaul Amoroto AlvaradoNo ratings yet
- Lecture7 ActualDocument57 pagesLecture7 ActualGhazwan Khalaf MohammadNo ratings yet
- Basic ConceptsDocument22 pagesBasic ConceptsTan Yi LiangNo ratings yet
- 3.2. Tensile Strength of ConcreteDocument21 pages3.2. Tensile Strength of ConcreteMacovei AlinNo ratings yet
- Environmental Engineering Concrete Structures: CE 498 - Design Project November 16, 21, 2006Document34 pagesEnvironmental Engineering Concrete Structures: CE 498 - Design Project November 16, 21, 2006Dory AzarNo ratings yet
- RCD ModulesDocument120 pagesRCD Modulesjeanyencrysta montesaNo ratings yet
- NS10-1Reinforced Concrete DesignDocument17 pagesNS10-1Reinforced Concrete DesignBhuidhar VermaNo ratings yet
- RCD Lecture 1Document26 pagesRCD Lecture 1Walter CatapangNo ratings yet
- Deep BeamsDocument19 pagesDeep BeamsTeresa Peter100% (1)
- Reinforced Concrete Lecture Notes University of HongKongDocument32 pagesReinforced Concrete Lecture Notes University of HongKongApril Ingram100% (4)
- Flexure 2Document15 pagesFlexure 2Ahmed EwisNo ratings yet
- Prestressed Concrete: Lecture No. (9) DateDocument29 pagesPrestressed Concrete: Lecture No. (9) DateNA PoNo ratings yet
- Design of Rectangular Reinforced Concrete BeamDocument7 pagesDesign of Rectangular Reinforced Concrete BeamsaadNo ratings yet
- JL 85 July August 7 PDFDocument25 pagesJL 85 July August 7 PDFkovaryNo ratings yet
- RCDDocument17 pagesRCDKim GabaynoNo ratings yet
- Eurocode 2 Lecture 1 - Design For FlexureDocument41 pagesEurocode 2 Lecture 1 - Design For FlexureKemoHNo ratings yet
- 6 Design For Deep Excavation Civil EngineeringDocument121 pages6 Design For Deep Excavation Civil EngineeringSathya Putra Wijaya100% (1)
- Unit I MCQ SD IiiDocument18 pagesUnit I MCQ SD IiiKiran BandeNo ratings yet
- RCC Lecture Series 4 2018-19Document33 pagesRCC Lecture Series 4 2018-19Mansa ArthurNo ratings yet
- Bending of R.C BeamsDocument23 pagesBending of R.C BeamsHarold Jackson MtyanaNo ratings yet
- Lecture 6.0 Flexural AnalysisDocument29 pagesLecture 6.0 Flexural AnalysisCharlene CardinozaNo ratings yet
- S 152 ContentDocument22 pagesS 152 ContentIgnatius SamrajNo ratings yet
- Analysis and Design of Prestressed Concrete Box Girder BridgeDocument18 pagesAnalysis and Design of Prestressed Concrete Box Girder BridgeYati AggarwalNo ratings yet
- Gate DoS (1997-2014)Document36 pagesGate DoS (1997-2014)Tejas PatilNo ratings yet
- Section 09 - Spiral ColumnDocument8 pagesSection 09 - Spiral ColumnmagdyamdbNo ratings yet
- WSD Beam DesignDocument11 pagesWSD Beam DesignThea Audrey SF DeritNo ratings yet
- RectangularTanks 25 3 2015 PDFDocument98 pagesRectangularTanks 25 3 2015 PDFHgagselim SelimNo ratings yet
- Pre-Stressed Concrete Lab: Ahsanullah University of Science & TechnologyDocument30 pagesPre-Stressed Concrete Lab: Ahsanullah University of Science & TechnologyMD MREDULNo ratings yet
- Ultimate Resistance of Reinforced Concrete Columns Strengthened With Angles and Battens: Theoretical Model and Experimental ValidationDocument15 pagesUltimate Resistance of Reinforced Concrete Columns Strengthened With Angles and Battens: Theoretical Model and Experimental ValidationUcok DedyNo ratings yet
- NS10 1concrete PDFDocument17 pagesNS10 1concrete PDFBoreirNo ratings yet
- PSCD A15 Lecture 1 PDFDocument13 pagesPSCD A15 Lecture 1 PDFLpthinh ThinhNo ratings yet
- Reinforced Concrete Design BS 8110Document15 pagesReinforced Concrete Design BS 8110Kutty Mansoor75% (4)
- Anclaje MurosDocument7 pagesAnclaje MurosPatricio LazcanoNo ratings yet
- Compression Strength of ConcreteDocument2 pagesCompression Strength of ConcreteRawaz KanabieNo ratings yet
- Ce6702 Pcs Civil Viist Au Unit IVDocument13 pagesCe6702 Pcs Civil Viist Au Unit IVKarthik SaravananNo ratings yet
- Appendix 11 Concrete Strength: CK, Cil CK CM CM CKDocument16 pagesAppendix 11 Concrete Strength: CK, Cil CK CM CM CKMaharAl-hasanNo ratings yet
- Design of One Way Slab-Basic Theory and Procedures-Dr. Latifee-16-Dec-2015v1Document18 pagesDesign of One Way Slab-Basic Theory and Procedures-Dr. Latifee-16-Dec-2015v1Ali M. MohammedNo ratings yet
- 06 DesignAndRetroffitingStrategyOfRCBCJoints PDFDocument0 pages06 DesignAndRetroffitingStrategyOfRCBCJoints PDFmy09No ratings yet
- BALANCEDDocument13 pagesBALANCEDJennifer dela CruzNo ratings yet
- Rule of Thumb For RC DesignDocument12 pagesRule of Thumb For RC DesignJeefry Arranguez50% (2)
- 3A - Flexural Behaviour of BeamsDocument57 pages3A - Flexural Behaviour of BeamsNoman Tariq MalkaniNo ratings yet
- Flexural Analysis of Beams: Concrete Structures DesignDocument24 pagesFlexural Analysis of Beams: Concrete Structures DesignAdam VinsonNo ratings yet
- Chapter 4 TrussesDocument68 pagesChapter 4 TrussesaisyahNo ratings yet
- Structural Concrete: The Commonwealth and International Library: Structures and Solid Body Mechanics DivisionFrom EverandStructural Concrete: The Commonwealth and International Library: Structures and Solid Body Mechanics DivisionNo ratings yet
- Some Mooted Questions in Reinforced Concrete Design American Society of Civil Engineers, Transactions, Paper No. 1169, Volume LXX, Dec. 1910From EverandSome Mooted Questions in Reinforced Concrete Design American Society of Civil Engineers, Transactions, Paper No. 1169, Volume LXX, Dec. 1910No ratings yet
- Steam TablesDocument20 pagesSteam Tablesajitsamal456No ratings yet
- Local Stresses WRC107Document19 pagesLocal Stresses WRC107naeand67% (3)
- Paint Coverage ConsumptionDocument2 pagesPaint Coverage ConsumptionSahilNo ratings yet
- Pipe Supports and RestraintsDocument44 pagesPipe Supports and RestraintsgchammaNo ratings yet
- Quick Check On Piping FlexibilityDocument8 pagesQuick Check On Piping Flexibilitysateesh chandNo ratings yet