362 Ch.

7 Itinerant Electron Magnetism

T = 0 (7.42) can be written as

(7.50)

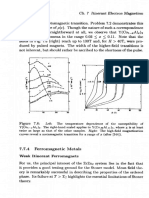
x(O)(Q)diverges logarithmically unless P ( E ) 3 0 as E + 0. It follows

that U2 = 0, i.e., for half-filled bands with the perfect nesting prop-
erty, an arbitrarily small interaction U > 0 causes a transition to a
two-sublattice antiferromagnetic state. We are going to see that the
antiferromagnetic state is insulating. Thus in these circumstances, the
metal-insulator transition occurs at U = 0.
When making the above statement, we were taking it for granted
that the q # Q susceptibilities are finite so that it is clear the q = Q
ordering is the dominant instability. A curious case is presented by
the half-filled, square lattice tight binding band. Here not only x ( Q )
diverges but, because of the logarithmic divergence of the density of
states (4.31), x(q = 0) too. We have a case of competing instabilities: it
appears that at an infinitesimal U > 0, the system might decide to go ei-
ther ferromagnetic, or antiferromagnetic. Which instability is stronger?
Strictly at T = 0, we should compare two infinite susceptibilities but
coming from finite temperatures, we can easily convince ourselves that
antiferromagnetism prevails (Problem 7.5).
Though (7.47) often gives a good idea of what can be expected to
happen, we should not forget that it was derived in a simple mean field
theory, and it is certainly not exact. We are speaking about Hartree-
Fock instabilities. Hartree-Fock theory is notorious for underestimating
the stability of the non-ordered, symmetrical ground state. We should
be especially cautious about ordering away from half-filling. It turns
out, however, that the prediction of the U = 0 metal-insulator transi-
tion for half-filled, perfectly nested bands is basically correct.
Problem 7.4 Derive x(O)(q) for the one-dimensional tight binding band.
Compare the divergence at q = 2 k to~ that obtained for free electrons.
Problem 7.5 Competing instabilities: For the half-filled square lattice tight
binding band at T = 0, x(O)(Q)and x ( O ) ( O ) diverge simultaneously. Decide
which divergence is stronger by doing a calculation at finite temperatures, and
taking the limit T + 0. (Hint: you can simplify the calculation by approxi-
mating the Fermi distribution by a piecewise linear function).
Compare the weak-coupling mean-field NEel temperatures for D = 2 di-
mensions, and D # 2.