REMOVABLE DISCONTINUITY ESSENTIAL DISCONTINUITY

A function is said to have a removable discontinuity at 𝑥 = 𝑐 if A function 𝑓(𝑥) is said to have an essential discontinuity at
𝑥 = 𝑐 if lim 𝑓(𝑥) DNE. This happens in two ways:
(a) lim 𝑓(𝑥) exists; and 𝑥→𝑐
𝑥→𝑐
(b) either 𝑓(𝑐) does not exist OR 𝑓(𝑐) ≠ lim 𝑓(𝑥). Case 1: The lim 𝑓(𝑥) DNE because the left-hand limit and the
𝑥→𝑐 𝑥→𝑐
right-hand limit both exist but are NOT equal. This discontinuity
A removable discontinuity (a.k.a Hole Discontinuity) may be
is called a jump essential discontinuity at 𝑥 = 𝑐.
removed by redefining 𝑓(𝑐) so that it will equal lim 𝑓(𝑥).
𝑥→𝑐
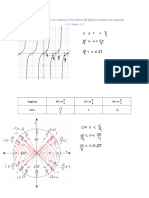
𝑥+1 if 𝑥 < 4
Example: Given ℎ(𝑥) = {
Examples: (𝑥 − 4)2 + 3 if 𝑥 ≥ 4.

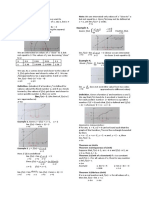
1. Below is the graph of 𝑔(𝑥). From previous lessons, we see that lim ℎ(𝑥) DNE because
𝑥→4

Notice that the limit exists as lim− ℎ(𝑥) = 𝟒 + 1 = 𝟓 and lim+ ℎ(𝑥) = (𝟒 − 4)2 + 3 = 𝟑.
𝑥→4 𝑥→4
𝑥 approaches 1, that is,
The graph of ℎ(𝑥)
lim 𝑔(𝑥) = 2. Furthermore,
𝑥→1 confirms this
𝑔(1) exists and it is equal to 1. discontinuity.
In symbols, 𝑔(1) = 1. There is indeed a
We have a removable “jump”. We may
discontinuity at 𝑥 = 1 because be tempted to
the limit value is not equivalent remove the
to the function value, that is, discontinuity but
𝑔(1) ≠ lim 𝑔(𝑥). doing so forces us
𝑥→1 to connect a
This discontinuity may be removed by redefining the vertical line
function 𝑔 at 𝑥 = 1. We simply transfer that point (1, 1) to the between (4, 5)
hole in (1, 2). Doing so, the hole gets filled and the discontinuity and (4, 3). The result will not be a function anymore as it
is removed! The redefinition is as follows: will fail the Vertical Line Test.

𝑔(𝑥) if 𝑥 ≠ 1 Case 2: If a function 𝑓(𝑥) is such that the lim 𝑓(𝑥) DNE
𝐺(𝑥) = { 𝑥→𝑐
2 if 𝑥 = 1 because either:
Does this make sense to you? Is 𝐺(𝑥) free of any discontinuity?
(i) lim− 𝑓(𝑥) = +∞, or (ii) lim− 𝑓(𝑥) = −∞, or
𝑥→𝑐 𝑥→𝑐

(iii) lim+ 𝑓(𝑥) = +∞, or (iv) lim+ 𝑓(𝑥) = −∞,

sin 𝑡 𝑥→𝑐 𝑥→𝑐
2. Let 𝑓(𝑡) = 𝑡
. Remember, this is one of the three special
then 𝑓(𝑥) is said to have an infinite essential discontinuity at
functions we discussed. Its graph looks like this:
𝑥 = 𝑐.
Example:
1
Given 𝑗(𝑥) = 𝑥 , 𝑥 ≠ 0. Its
graph is shown here. Notice
It is easy to see that the graph of 𝑓(𝑡) is continuous everywhere the permanent discontinuity
except at 𝑥 = 0. The discontinuity at 𝑥 = 0 is another example at 𝑥 = 0 because
of a removable discontinuity because the limit value of 𝑓(𝑡) as lim− 𝑓(𝑥) = −∞. Also,
𝑥→0
𝑡 approaches 0 exists, that is, lim 𝑓(𝑡) = 1. But, the function lim 𝑓(𝑥) = +∞.
𝑡→0 𝑥→0+
value of 𝑓(𝑡) at 𝑡 = 0 does not exist.
In general, an infinite limit implies a vertical asymptote and
The discontinuity may be removed by redefining the function: a discontinuity.
sin 𝑡
𝐹(𝑡) = { 𝑡 if 𝑡 ≠ 0
1 if 𝑡 = 0.

Does this make sense to you? Is 𝐹(t) free of any discontinuity?