EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

Homework 4 - Solutions
Note: Each part of each problem is worth 3 points and the homework is worth a total of 42 points.

1. State Space Representation To Transfer Function

Find the transfer function and poles of the system represented in state space below.
   
8 −4 1 −4
ẋ = −3 2 0  x + −3 u(t)
   

5 7 −9 4
 
h i 0
y = 2 8 −3 x; x(0) = 0
 

Solution: G(s) = C(sI − A)−1 B

 
(s − 2)(s + 9) −(4s + 29) (s − 2)
1
(sI − A)−1 = 3  −3s − 27 (s2 + s − 77) −3
 
s − s2 − 91s + 67

5s − 31 7s − 76 (s2 − 10s + 4)
  
(s − 2)(s + 9) −(4s + 29) (s − 2) −4
−1 1 h i
2
C(sI−A) B = 3 2 8 −3  −3s − 27 (s + s − 77) −3  −3
  
s − s2 − 91s + 67 2
5s − 31 7s − 76 (s − 10s + 4) 4

−44s2 + 291s + 1814

G(s) =
s3 − s2 − 91s + 67

2. Transfer Function Analysis For Mechanical Systems

For the system shown below, do the following:
(a) Find the transfer function G(s) = X(s)/F (s).
(b) Find ζ, ωn , % OS, Ts , Tp and Tr .

Solution:
(a) Writing the equation of motion yields, (5s2 +5s+28)X(s) = F (s). Solving the transfer function,
1
X(s) 1
= 2 = 2 5 28
F (s) 5s + 5s + 28 s +s+ 5

Rev. 1.0, 02/23/2014 1 of 9

EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

(b) Clearly, ωn2 = 28/5 rad/s and 2ζωn = 1. Therefore, ωn = 2.37, ζ = 0.211.
4
Ts = = 8.01 sec
ζωn
π
Tp = p = 1.36 sec
ωn 1 −√ζ 2
2
%OS = e−ζπ/ 1−ζ × 100 = 50.7%
Tr = ω1n (1.76ζ 3 − 0.417ζ 2 + 1.093ζ + 1) = 0.514 sec

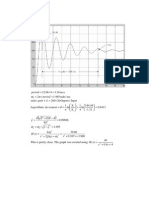
3. Transfer Function From Unit Step Response

For each of the unit step responses shown below, find the transfer function of the system.

Solution:
K
(a) This is a first-order system of the form: G(s) = . Using the graph, we can estimate the
s+a
1 K
time constant as T = 0.0244 sec. But, a = = 40.984, and DC gain is 2. Thus = 2. Hence,
T a
K = 81.967.
Thus,
81.967
G(s) =
s + 40.984
K
(b) This is a second-order system of the form: G(s) = . We can estimate the
s2 + 2ζωn s + ωn2
percent overshoot and the settling time from the graph.
%OS = (13.82−11.03)
11.03 × 100 = 25.3%
Ts = 2.62sec

Rev. 1.0, 02/23/2014 2 of 9

EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

We can now calculate ζ and ωn from the given information.

− ln(%OS/100)
ζ=q = 0.4
2 2
π + ln (%OS/100)
4
ωn = = 3.82
ζTs
K
DC Gain = 11.03. Therefore, 2 = 11.03. Hence, K = 160.95. Substituting all values, we get
ωn

160.95
G(s) =
s2 + 3.056s + 14.59

K
(c) This is a second-order system of the form: G(s) = . We can estimate the
s2 + 2ζωn s + ωn2
percent overshoot and the peak time from the graph.
%OS = (1.4−1.0)
1.0 × 100 = 40%
Tp = 4
We can now calculate ζ and ωn from the given information.

− ln(%OS/100)
ζ=q = 0.28
2 2
π + ln (%OS/100)
π
ωn = p = 0.818
Tp 1 − ζ 2
K
DC Gain = 1.0. Therefore, 2 = 1.0. Hence, K = 0.669. Substituting all values, we get
ωn

0.669
G(s) =
s2 + 0.458s + 0.669

4. State Space Analysis

A system is represented by the state and output equations that follow. Without solving the state
equation, find the characteristic equation and the poles of the system.
   
0 2 3 0
ẋ = 0 6 5 x + 1 u(t)
   

1 4 2 1
h i
y= 1 2 0 x

Solution:      
1 0 0 0 2 3 s −2 −3
(sI − A) = s 0 1 0 − 0 6 5 =  0 s − 6 −5 
     

0 0 1 1 4 2 −1 −4 s − 2

Characteristic Equation: det (sI − A) = s3 − 8s2 − 11s + 8

Factoring yields poles: 9.111, 0.5338 and − 1.6448

Rev. 1.0, 02/23/2014 3 of 9

EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

5. Block Diagram To Transfer Function

Reduce the system shown below to a single transfer function, T (s) = C(s)/R(s).

Solution: Push G2 (s) to the left past the summing junction.

Collapse the summing junctions and add the parallel transfer functions.

Rev. 1.0, 02/23/2014 4 of 9

EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

Push G1 (s)G2 (s) + G3 (s) to the right past the summing junction.

Collapse the summing junctions and add feedback paths.

Applying the feedback formula,

G3 (s) + G1 (s)G2 (s)

T (s) =
1 + H(s)[G3 (s) + G1 (s)G2 (s)] + G2 (s)G4 (s)

6. Block Diagram To Transfer Function

For the system shown below, find the poles of the closed-loop transfer function, T (s) = C(s)/R(s).

Rev. 1.0, 02/23/2014 5 of 9

EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

Solution: Push 2s to the left past the pickoff point and combine the parallel combination of
2 and 1/s.

Push (2s + 1)/s to the right past the summing junction and combine summing junctions.

Hence,
2(2s + 1) s 5
T (s) = where Heq = 1 + + .
1 + 2(2s + 1)Heq (s) 2s + 1 2s
4s2 + 2s
T (s) =
6s2 + 13s + 5

7. Finding Constants To Meet Design Specifications

For the system shown below, find the values of K1 and K2 to yield a peak time of 1.5 seconds and
a settling time of 3.2 seconds for the closed loop system’s step response.

Rev. 1.0, 02/23/2014 6 of 9

EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

Solution: The closed-loop transfer function is given by:

10K1
T (s) =
s2 + (10K2 + 2)s + 10K1

4 p π
We know, ζωn = = 1.25. And ωn 1 − ζ 2 = = 2.09. Therefore, poles are at −ζωn ±
Ts Tp
p √ √
ωn 1 − ζ 2 = −1.25 ± j2.09. Hence, ωn = 1.252 + 2.092 = 10K1 and (10K2 + 2)/2 = 1.25.
Therefore, K1 = 0.593 and K2 = 0.05.

8. Signal-Flow Graphs
Draw a signal-flow graph for the following equation.
   
0 1 0 0
ẋ =  0 0 1  x + 0 r(t)
   

−2 −4 −6 1
h i
y= 1 1 0 x

Solution:

x˙1 = x2
x˙2 = x3
x˙3 = −2x1 − 4x2 − 6x3 + r
y = x1 + x2

9. Signal-Flow Graphs
Using Mason’s rule, find the transfer function, T (s) = C(s)/R(s), for the system represented by the
following figure.

Rev. 1.0, 02/23/2014 7 of 9

EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

Solution:
Closed-loop gains: G2 G4 G6 G7 H3 ; G2 G5 G6 G7 H3 ; G3 G4 G6 G7 H3 ; G6 H1 ; G7 H2

Forward-path gains: T1 = G1 G2 G4 G6 G7 ; T2 = G1 G2 G5 G6 G7 ; T3 = G1 G3 G4 G6 G7 ; T4 = G1 G3 G5 G6 G7

Nontouching loops 2 at a time: G6 H1 G7 H2

∆ = 1 − [H3 G6 G7 (G2 G4 + G2 G5 + G3 G5 ) + G6 H1 + G7 H2 ] + [G6 H1 G7 H2 ]

∆1 = ∆2 = ∆3 = ∆4 = 1

T1 ∆1 + T2 ∆2 + T3 ∆3 + T4 ∆4
T (s) =
∆
G1 G 2 G4 G 6 G7 + G1 G 2 G5 G6 G7 + G1 G3 G4 G6 G7 + G1 G3 G5 G6 G 7
T (s) =
1 − H3 G6 G7 (G2 G4 + G2 G5 + G3 G4 + G3 G5 ) − G6 H1 − G7 H2 + G6 H1 G7 H2

10. State Space Representation and Signal-Flow Graphs

Represent the system shown below in state space form and draw its signal-flow graph.

s+3
G(s) =
s2 + 2s + 7

Solution: Writing the state equations,

x˙1 = x2
x˙2 = −7x1 − 2x2 + r
y = 3x1 + x2
" # " #
0 1 0
ẋ = x+ r
−7 −2 1
h i
y= 3 1 x

Rev. 1.0, 02/23/2014 8 of 9

EE C128 / ME C134 Spring 2014 HW4 - Solutions UC Berkeley

11. Canonical Forms

Represent the system given in Problem 10 in controller canonical form and observer canonical form.
Solution:
Controllable canonical form: " # " #
−2 −7 1
ẋ = x+ r
1 0 0
h i
y= 1 3 x

Observable canonical form: " # " #

−2 1 1
ẋ = x+ r
−7 0 3
h i
y= 1 0 x

Rev. 1.0, 02/23/2014 9 of 9