Trigonometry II and Circle Theorem

CXC Mathematics General Proficiency Trigonometry II and Circle Theorem
Topics are object is 58.5 m away from the building on

TRIGONOMETRY a line directly beneath the person.
1. angle of elevation / angle of depression

2. Three dimensional problems
3. Bearings
4. The sine rule and the cosine rule
CIRCLE THEOREMS
1. Circle review
2. Circle Theorems 2. the angle of elevation of the line of sight of

a person whose eye is 1.7 m above the
ground, and is looking at the top of a tree
which is 27.5 m away on level ground and
TRIGONOMETRY 18.6 m high.
Angle of Elevation / Angle of

Depression
An angle of elevation is always measured upwards

from a horizontal line.
3. From the top of a vertical cliff 40 m high,

the angle of depression of an object that is
level with the base of the cliff is 34º.
How far is the object from the base of the

An angle of depression is always measured cliff?
downwards from a horizontal line.
Solution:
Let x m be the distance of the object from the base of

the cliff.
Examples:
1. A person stands at the window of a building

so that his eyes are 12.6 m above the level
ground in the vicinity of the building. An
Revision notes  Paper 2 Section II Page | 243
= 17.95
 APO = angle of depression = 34°
(alternate angle are equal) The height of the tree is approximately 17.95 m.
opppsite
tan (angle) = adjacent  tan ratio
Three dimensional problems
from Δ APO
40 Examples:
tan (34°) =  transpose for x
x
1. Find the length of the diagonal, and angle
40
x = tan 34
 tan (34°) = 0.675 between the diagonal AP and the base of a
cube of side-length 5 cm, as shown.
40
x = = 59.3
0.675
So, the object is 59.30 m from the base of the cliff.
4. A man who is 2 m tall stands on horizontal

ground 30 m from a tree. The angle of
elevation of the top of the tree from his eyes
is 28˚.
Estimate the height of the tree.

Solution:
Solution:
Let the height of the tree be h. Sketch a diagram to

represent the situation.
Calculating the length of the diagonal AP
opppsite
tan (angle) = adjacent  tan ratio
h  2
tan 28˚ =  transpose for h
30
h – 2 = 30 tan 28˚
h = (30 × 0.5312) + 2  tan 28˚ = 0.532

By Pythagoras' Theorem and triangle ACD,

A bearing is an angle, measured clockwise from the
north direction.
Example:
1.
x2 = 52 + 52 = 25 + 25 = 50
x = 50 = 7.07
The bearing of B from A is 050 º
Note that 3 figures are always given for bearings.
2.
AP2 = 52 + 7 .072
= 25 + 49.9849 = 74.9849
AP = 74.9849 = 8.66
The bearing of A from B is 225º.
 The length of AP is approximately 8.66 cm.
Calculating the angle between the diagonal AP and

3. A, B and C are three ships. The bearing of A
the base of a cube
from B is 045º. The bearing of C from A is
135º. If AB = 8 km and AC = 6 km, what is
O
Tan  =  tan ratio the bearing of B from C?
A
from Δ ACP
1  5 
 = Tan   = tan-1 (0.707)
 07 
7.
= 35.3°
So, the angle between the diagonal AP and the base

of a cube is 35.3°
Bearings Solution:
1  8 
a 2  b 2  c 2   2 bc   cos A or
C = tan Tan   = tan-1 (1.33)
6 b 2
 a c
2 2
  2 ac   cos B  or
= 53.1º c 2  a 2  b 2   2 ab   cos C 
to find an angle, you can write as:

y = 180º  135º = 45º (interior angles)
b2  c2  a2
Working out the left side: cos A  or
2 bc
x = 360º  (53.1º + 45º) (angles round a point) cos B 
a2  c2  b2
or
2 ac
= 261. 9 ≈ 262º (to the nearest whole number) a2  b2  c2
cos C  or
2 ab
The Sine rule and the Cosine rules

The cosine rule can be applied when given:
Triangles without right angles can be solved by
two sides and one angle in-between, or,
applying the sine rule or the cosine rule or both:
the length of all three sides
The area of triangles without right angles can be computed by

applying:
1
Area = bc sin A
2
The sine rule 1
= ac sin B
2
The sine rule is a relationship between the length 1
of the side and the sine of its angle. = ab sin C
2
a b c
 
sin A sin B sin C
to find an angle, you can write this as:
sin A sin B sin C

 
a b c
The sine rule can be applied when given:
two angles and one side, or,
two sides and one angle opposite to one of the

sides.
The cosine rule

Examples:
12  0.707 Working out to the
AC 
1. In the diagram below, ACX is a straight line. 0 .5 nearest whole number
BC = 12 cm,  BAC  30 and

 ABC  14.5 = 17 cm Ans.
(b) Calculating the area of Δ ABC
A sketch
With two sides and an
angle in-between the
sides, the formula
Calculate: Area =
1
(a) the length of AC, to the nearest whole ab sin C
2
number,
may be applied
(b) the area of Δ ABC, Applying the formula:
(c) the value of the angle  . 1

Area = ab sin C Substituting:
2
Solution: =
1
(a) Calculating the length of AC 12  17  sin 14
2
A sketch =
1
12  17  0.242
2
With two angles and
one side, the sine rule = 24.7 cm² Ans.
may be applied
(c) Calculating the value of the angle .

Applying sine rule:
AC BC A sketch
 Substituting:
sin B sin A
AC

12 angle 
sin 136 sin 30
AC 12
 transposing angle  = 30  136 Substituting:
0.707 0.5
= 166º Ans.

2. the diagram below, not drawn to scale,

shows Δ PQR with PQ = 10.9 cm, 0.946  10.9
sin R 
15.2
PR = 15.2 cm and  PQR  109 .
Working out the angle
= 0.678 to the nearest whole
 R  sin 1 (0.678)
 PRQ   R
 PRQ = 43º Ans.
Calculate:
(a) the size of  PRQ, to the nearest whole (b) Calculating the length of QR, to one decimal
place:
number,
A sketch
(b) the length of QR, correct to one decimal
With three angles and
place,
two sides, the sine rule
or the cosine rule may
(c) the area of Δ PQR. be applied
Solution: Applying sine rule:
QR PR
(a) Calculating the size of  PRQ, to the nearest  Substituting:
sin P sin Q
whole number:
A sketch QR 15.2

sin 28 sin 109
angle opposite, the sine QR 15.2
 transposing
rule may be applied 0.469 0.946
Applying sine rule: 15.2  0.469 Working out to one

QR 
0.946 decimal place
sin R sin Q
 Substituting:
PQ PR = 7.5 cm Ans.
sin R sin 109


10.9 15.2
sin R 0.946
 Transposing:
10.9 15.2

(c) Calculating the area of Δ PQR With two sides and an

angle in-between the
A sketch sides, the formula
With all sides and
Area =
angles, the formula
1
ab sin C
Area = 2
1 may be applied
ab sin C
2 Applying the formula:
may be applied
Applying the formula: 1

Area = ab sin C Substituting:
2
1 =
Area = 10.9  7.5  sin 109
2
1
 20  15  sin 110 
= 2
1 =
10.9  7.5  0.946
2 1
 20  15  0.940
2
= 38.7 cm² Ans.
= 141 cm² Ans.
3. In the diagram below, not drawn to scale,

A, B and C are three towns. There are joined
by straight roads. (b) Calculating the distance AB
A sketch
angle in-between, the
cosine rule may be
applied
Applying sine rule:

The distance AC = 20 km, BC = 15 km and
 ACB  110  . Calculate:
c 2  a 2  b 2   2 ab   cos C  Substituting:
(a) the area of Δ ABC,
(b) the distance AB.
c 2  20 2  15 2   2  20  15  cos110
(c) the size of  CAB .
c 2  400  225   600    0.342 

Solution:
(a) Calculating the area of Δ ABC c 2  400  225  205.2 = 830.2
A sketch
c  830.2 = 28.8 AB = c

AB = 28.8 km Ans. (c) F.
(c) Calculating the size of  CAB

Solution:
A sketch (a) Calculating the size of angle D

With two sides and two
angles, the sine rule or A sketch
the cosine rule may be
applied
With three sides, the
Applying the cosine rule: cosine rule may be
applied
b2  c2  a2
cos A  Substituting:
2 bc
Applying the cosine rule:
20 2  28.8 2  15 2
= e2  f 2  d 2
2  20  28.8 cos D  Substituting:
2 ef
400  830  225

= 312  53 2  47 2
1152 =
2  31 53
= 0.872 inversing
961  2809  2209
=
3286
 A  cos 1 (0.872) = 29.3º  CAB   A
= 0.475 inversing
 CAB = 29.3º Ans.
 D  cos 1 (0.475)
4. A triangular sheet of cardboard, DEF, has

sizes whose lengths are DE = 31 cm, DF = = 61.6º Ans.
53 cm and EF = 47 cm.
(b) Calculating the size of angle E
A sketch
With three sides and

one angle, the sine rule
or the cosine rule may
be applied
Calculate the size of angle:
(a) D, Applying the cosine rule:
(b) E, d 2  f 2  e2
cos E  Substituting:
2 df

=
47 2  53 2  312 CIRCLE THEOREM
2  47  53
2209  2809  961 Circle review

=
4982
= 0.814 inversing Angles in an isosceles triangle
Base angles of an
 E  cos 1 (0.814)
isosceles triangle are
equal:
= 35.5º Ans.
z = y
180  x
=
2
(c) Calculating the size of angle F
x = 180  2 y
A sketch = 180  2 z
With two angles, the Angles in a transversal diagram

sum of angles in a
triangle may be
applied x = y
alternate angles.
Applying the sum of angles in a triangle:
F  180   61.6  35.5  z = y
corresponding
= 180  97.1
angles.
= 82.9º Ans.
Circle Theorems
1. The angle at the centre and the angle at the

circumference
The angle at the centre is

twice the angle at the
circumference when
triangles lie on the same
chord (chord AB):
x = 2y

2. Angles at the circumference subtended on

the same chord
Two tangents to a
circle from a
common point are
The angles at the
equal:
circumference are equal
when triangles lie on the AT = BT
same chord (chord AB):
x = y
5. Alternate Segment
3. Angle in a semi-circle The angle between the
tangent and chord at
the point of contact is
The angle in a equal to the angle in
semicircle is always a the alternate segment:
right angle:
y =w
x = 90º
z =x
Proof
higher Proof
w =x
w =x z =y
z =y x  y = 90º
6. Cyclic quadrilateral
4. Tangents A cyclic quadrilateral is a quadrilateral whose
vertices all touch the circumference of a circle.
A tangent to a circle is a straight line which touches
the circle at only one point (so it does not cross the
circle- it just touches it).
The opposite interior
angles add up to 180º:
The angle between the x  z = 180º

tangent and the radius
of the circle is 90º : w  y = 180º
x = 90º

Proof Solution:
(a) angle ADB

The exterior angle is
equal to the interior
opposite angle:
The angle at the centre is
twice the angle at the
A = y circumference when
triangles lie on the same
B = z chord.
C = w
98
 ADB  = 49º Ans.
D =x 2
Examples: (b) angle ABO
1. In the diagram, not drawn to scale, A, B, C

and D are points on a circle with centre O.
Base angles of an isosceles
triangle are equal:
180  98
 ABO  = 41º Ans.
2
(c) angle BAO
 AOB = 98º and D CB = 110º.

Base angles of an
isosceles triangle are
Calculate, giving a reason for your answers, equal.
the measure of angle:
(a) ADB  BAO   ABO = 41º Ans.
(b) ABO
(d) angle DAB
(c) BAO
(d) DAB
The opposite interior angles of a
(e) DAO cyclic quadrilateral angles add
up to 180º.
 DAB  180  110  = 70º Ans.

(e) angle DAO
The angle between the

tangent and the radius
of the circle is 90º
Sum of adjacent
angles.
 BEO  90  38 = 52º Ans.
 DAO  70  41 = 29º Ans. (b) Calculating the angle BCE
2. In the diagram, not drawn to scale, DEF is The angle between the
a tangent to the circle ABCE, with centre O. tangent and chord at the
The measure of angle BEF is 38 º. point of contact is equal
to the angle in the
alternate segment.
 BCE  38 Ans.
(c) Calculating the angle BAE

angles of a cyclic
Calculate, giving a reason for your answers, quadrilateral add up
the size of each of the following angles: to 180º.
(a) BEO
 BAE  180  38 = 142º Ans.
(b) BCE
(c) BAE
(d) angle BOE
(d) BOE
The angle at the
centre is twice the
Solution: angle at the
circumference when
triangles lie on the
(a) angle BCE same chord.
 BOE  2  38 = 76º Ans.
3. In the diagram, not drawn to scale, AB is a

tangent to the circle ACDE, so that
CAB  50 and  ABC  30 . (b) angle ACE

BCE is a straight line
 ACE  180  100 The angles on a

straight line at a point
Calculate, giving a reason for each answer, = 80º Ans. sum up to 180º
the measure of angle:
(a) ACB
(d) angle CAE
(b) ACE
(c) AEC
(d) CAE
(e) EDC
The angle between the tangent

Solution:  CAE  50 and chord at the point of contact
Ans. is equal to the angle in the
(a) angle ACB alternate segment.
(d) angle CAE
 ACB  180  (30  50The

) sum of angles
in a triangle equals
= 100º Ans. 180º  CAE  180  (80  50The
) sum of angles
in a triangle equals
= 50º Ans. 180º

(e) angle EDC 2.
(a) In the diagram below, not drawn to scale,

RST is a horizontal straight line and UR
represents a vertical pole.

 EDC  180  50 angles of a cyclic
= 130º Ans. quadrilateral add up to
180º
Examination Questions (to do)

Attempt ALL questions. ST = 15 m,  UST = 120° and
 STU = 40°.
All working must be clearly shown.
Calculate
TRIGONOMETRY
(a) the angle of elevation of U from S.
1. The figure SJKM below, not drawn to scale,
is a trapezium with SJ parallel to MK, angle (b) the length of UT.
MJK = 124, MSJ = 136, and SM = SJ = 50 (c) the length of RU
metres.

ST = 5 cm, TW = 9 cm and angle STW =
52°.
(a) Calculate the size of :
(i) angle SJM
(ii) angle JKM
(b) Calculate expressing your answer to correct Calculate

to ONE decimal place, the length of
(a) the length of SW
(i) MJ
(b) the area of ∆ STW .
(ii) JK
4. In the diagram below, not drawn to scale, 6. The diagram below, not drawn to scale,
TL is a vertical tower, and LMN is a straight shows parallelogram EFGH in which
line on a horizontal plane. EF = 6 cm, EH = 4.2 cm, and angle
FEH = 70°
The angles of elevation of T, the top of the
tower from the points M and N are 65° and
42° respectively. The distance of M from N
is 15 m.
Calculate
(a) the length of the diagonal HF
(b) the area of the parallelogram EFGH.

(a) Using triangle MNT, show that the length of
MT to the nearest metre, is 26 m. 6. The diagram below, not drawn to scale,
shows the journey of a ship which sailed
(b) Hence, calculate the height of the tower, TL. from
Port K to Port L. Port L is located 28 km

3 East and 16 km South of Port K
5. Given that Sin θ = , 0° ≤ θ ≤ 90°.
2
Calculate, giving your answer correct to 3

significant figures:
(a) Find the value of θ.
(a) the distance KL
(b) Calculate the area of triangle CDE
(b) the bearing of Port L from Port K.
(c) Calculate the length of the side EC

7. The figure below, not drawn to scale, (b) the height of the tower, BC
represents the journey of an aircraft flying
from Y to X and then from X to Z.
9. TK is a vertical tower, 10 metres high,
standing on a horizontal plane QKS.
Q and S are markers placed on the

horizontal plane and angle QKS measures
112°.
The angles of elevation of the top of the

The bearing of X from Y is 035°. tower, T, from Q and S are 14° and 21°
The bearing of Z from X is 125°. respectively.
Z is due east of Y.
(a) Copy and complete the diagram, showing

CLEARLY the bearings 035° and 125°.
(b) Determine the size of the angle YXZ.
(c) Calculate, to the NEAREST whole number,

the distance YZ given that YX = 100 km.
8. The diagram below, not drawn to scale,

shows a vertical pole, AD, and a vertical
(a) Draw a diagram to represent the
tower, BC standing on horizontal ground
information, CLEARLY showing
XABY. The height of the pole is 2.5 metres.
From the point D, the angle of depression of (i) the line segment which represents 10
B is 5° and the angle of elevation of C is metres.
20°. DE is a horizontal line
(ii) the angles whose measures are 14°,
21° and 112°
(iii) TWO right angles.
(b) Calculate, to the NEAREST metre, the

distance
(i) QK
Calculate, to one decimal place,
(ii) SK
(a) the horizontal distance AB.
(iii) QS.

12. Three cricketers. A, B and C are positioned

(c) A vertical pole 4 m high is placed at Q. An on a cricket ground so that:
instrument placed on the top of this pole
measures the angle of elevation of the top of A, the bowler is 22 metres south of B, the
the tower. Calculate the size of this angle of batsman. C, the fielder is on a bearing of
elevation. 205° from B. The distance between C and B
along a straight line is 36 metres
10.
(a) Draw a diagram showing the positions of A,
(a) Draw a diagram to represent the information B and C.
given below.
(b) On your diagram show:
Show clearly the north line in your diagram.
(i) the north direction
Town F is 50 km east of town G. (ii) the points A, B and C
Town H is on a bearing of 040° from town F. (iii) the distances 22 m and 36 m
The distance from F to H is 65 km. (iv) the bearing of 205°.

(c) For the diagram in Part (a):
(b) Calculate, to the nearest kilometre, the actual
(i) State the size of the angle CBA.
distance GH.
(ii) Calculate, to the NEAREST metre,
(c) Calculate, to the nearest degree, the bearing the distance AC.
of H from G.
(iii) Calculate, to the NEAREST degree,
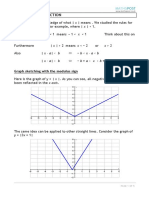
11. Given that y  2  cos x , the bearing of A from C.
(a) copy and complete the table below. (iv) How far east must C move if he is to
be in line with A and B?
x 0° 30° 60° 90° 120° 150° 180°
y 1.1 1.5 2.5 3 13. A boat leaves a dock at point A and travels
for a distance of 15 km to point B on a
bearing of 135°.
(b) Using a scale of 2 cm to represent 30° on
the x-axis, and 1 cm to represent 0.2 on the The boat then changes course and travels for
y-axis, draw the graph of y  2  cos x a distance of 8 km to point C on a bearing of
for 0°  x  180°. 060°.
(c) Using the graph, or otherwise, determine the (a) Illustrate the above information in a clearly
value of x for which 2  cos x  1.8 labelled diagram.

The diagram should show the

(c) The ship leaves Port T and travels due west
(i) north direction to a point X which is due north of R.
(ii) bearings 135° and 060° (i) Show on your diagram the journey
from T to X .
(iii) distances 8 km and 15 km.
(b) Calculate (ii) Calculate the distance T X
(i) the distance AC 15. The diagram below shows a map of Baytime
drawn on a grid of 1 cm squares.
(ii)  BCA
The scale of the map is 1:100 000.
(iii) the bearing of A from C.
14. A ship leaves Port R, sails to Port S and then

to Port T.
The bearing of S from R is 112°.

The bearing of T from S is 033°.
The distance RT is 75 km and the distance
RS is 56 km.
(a) Draw a diagram showing the journey of the

ship from R to S to T. Show on your
diagram
(a) Find the nearest km, the shortest distance
(i) the North direction between Rose Hall and South Port.
(ii) the bearings 112° and 033° (b) Determine the bearing of South Port from
Spring Hall.
(iii) the points R, S and T
(iv) the distances 75 km and 56 km 16. A ship leaves a harbour, H, and sails to a
port, A, 45 km away on a bearing of 064°.
The ship then changes course and sails to
(b) Calculate
another port, B, 60 km away on a bearing of
(i) the size of angle RST 285°.
(ii) the size of angle RTS (a) Sketch the ship's journey, clearly showing
(iii) the bearing of R from T. (i) the north direction

(ii) the bearings 064°and 285° (c) Calculate, in metres, the distance RS, giving
your answer correct to 2 significant figures.
(iii) the points H, A and B.
(b) Calculate
19. A ship leaves a harbour, H, and sails to a
(i) the distance HB, in km, to 2 decimal
port, A, 45 km away on a bearing of 064°.
places
The ship then changes course and sails to
another port, B, 60 km away on a bearing of
(ii) the bearing of H from B, to the
285°.
nearest degree.
(a) Sketch the ship's journey, clearly showing:
17. The base, N, of an antenna rests on a
horizontal ground. The angle of elevation to (i) the north direction
the top R, from a point H on the ground is
42º. The angle of elevation of R from a (ii) the bearings 064°and 285°
second point on the ground G, 6 m closer to
(iii) the points H, A and B.
N is 53.2º.
(c) Calculate
(a) Draw a diagram to show the information
above, labeling all given points, distances (i) the distance HB, in km, to 2 decimal
and angles. places
(b) Calculate, to 3 significant figures (ii) the bearing of H from B, to the

nearest degree
(i) the length RG
(ii) the height RN, of the antenna. 20. Points O, P and Q are in the same horizontal
plane. P is 15 m away from O on a bearing
(c) A third point, C, lies on the ground 5.4m of 040° from O. Q is on a bearing of 130°
from N. The angle of depression of C from from O, and PQ = 17 m.
R is x degrees. Calculate to the nearest
degree, the value of x. (a) Sketch a diagram to show the positions of
O, P and Q. Clearly indicate North on your
18. Q, R and S three points on a level ground. S diagram.
is due east of Q and QS = 45 metres. The
bearing of R from Q is 042º and the bearing (b) Calculate the distance OQ.
of S from R is 110º
(a) Draw a diagram to show this information

indicating clearly the bearings and the
distances given.
(b) Calculate the bearing of R from S.

21. Q, R and S are three points on level ground. AB = 4.2 m, BTF = 28° and TAF = 50°.
S is due east of Q and QS = 45 metres. The TFB and TFA are right angles.
bearing of R from Q is 042° and the bearing
of S from R is 110°. (a) Calculate
(a) Draw a diagram to show this information (i) the lengths of FB and FA, giving
indicating clearly the bearings and distances your answers to 3 significant figures
given.
(ii) the size of angle AFB, to the nearest
(b) Calculate the bearing of R from S. degree.
(c) Calculate, in metres, the distance RS, giving (iii) the bearing of B from F.
your answers correct to 2 significant figures.
(b) Given that the area of triangle BTA = 28.1
m² and AT = 15.7 m, calculate the size of
22. A ship leaves port P and sails to port Q, 50 angle BTA.
km away on a bearing of 124°. From Q, the
ship travels to port R on a bearing of 320°.
24. A cross-country race covers a course which
(a) Given that the bearing of R from P is 025°, takes the shape of a triangle, KLM. Runners
draw a carefully labelled diagram to are to start at K and run 4 1cm due north to a
represent the journey of the ship. point, L.
(b) Determine the bearing of P from R. From L, they are to run 5 km on a bearing of
300° to a point, M, and then run directly
(c) Calculate, giving your answer to 2 decimal back to K.
places, the distance between P and R.
(a) Draw a diagram to represent the triangular
course carefully labeling:
23. The diagram above, not drawn to scale,
shows a pole TF, 12 m high, standing on (i) the points K, L and M
level ground. The points A, F and B lie in
the same horizontal plane. (ii) the distances 4 km and 5 km
(iii) the north direction
(iv) the bearing 300°.
(b) Calculate:
(i) the distance KM in km
(ii) the bearing of M from K.

GEOMETRY (a) Calculate, giving reasons for your answer,

the size of
1. In the diagram below, not drawn to scale, O (i) angle MCD
is the centre of the circle. Angle AOB = 80°
and AB = 12 cm. (ii) angle CMD.
(b) Explain why the quadrilateral OCMD is

cyclic.
(c) Given that the radius of the circle shown in

the diagram above is 6.5 cm, calculate:
(i) the area of triangle OCD
(ii) the area of the shaded segment of the

circle.
3. The diagram below, not drawn to scale,

Calculate, giving your answer correct to 2 shows a circle, centre O, radius 15 cm. The
decimal places: length of the minor arc LM is 9 cm and LN
is a tangent to the circle. OMN is a straight
(a) the radius of the circle line.
(b) the area of the minor sector AOB
(c) the area of the shaded region.

MC and MD are tangents of the circle whose
centre is at O. Angle COD measures 96°.
Calculate:
(a) the size of angle MOL
(b) the area of the minor sector OML
(c) the area of the shaded region.

4. In the diagram, not drawn to scale, O is the (b) Determine the area, in cm2, of
centre of the circle. Angle AOB = 120° and
the radius of the circle is 6 cm. (i) the base
(ii) the curved surface area
(iii) the total surface area of the cone.
(c) Find the volume of the cone.
6. In the diagram below, not drawn to scale, P

and Q are midpoints of the sides XY and XZ
of the triangle XYZ.
Calculate, giving your answers to 2 decimal

places:
(a) the area of triangle OAB
(b) the area of the shaded region.
5. The diagram below, not drawn to scale, Given that XP = 7.5 cm, XQ = 4.5 cm and
represents right circular cone with a slant the area of triangle XPQ = 13.5 cm2,
height of 20 cm and angle AOC = 50°. calculate:
(a) the size of angle PXQ, expressing your

answer in correct two the nearest degree.
(b) the area of the XYZ
(a) Calculate, in cm:
(i) the length of the diameter AC
(ii) the length of the arc AC
(iii) the perpendicular height of the cone.

7. In the diagram below, not drawn to scale, 9. In the diagram below, not drawn to scale,
ABT is a tangent to the circle BEDC, centre DEF is a tangent to the circle ABCE, with
O. AEC is a straight line through the centre centre O. The measure of angle BEF is 38°.
O, with angle ECB = 35°.
Calculate, giving reasons for your answers,

the sizes of the following angles: Calculate, giving reasons for your answers,
the size of EACH of the following angles:
(a) EDB
(a)  BEO
(b) BEC
(b)  BCE
(c) CBT
(c)  BAE
(d) BAE
(d)  BOE
8. In the diagram below, VWZ and WXYZ are
two circles intersecting at W and Z. SVT is a 10. In the diagram below, not drawn to scale,
tangent to the circle at V, VWX and VZY are AB and BC are tangents to the circle, centre
straight lines,  TVY = 78° and O. The radius of the circle is 9 cm and angle
 SVX = 51°. ABC = 66°.
Calculate, giving reasons for each step of

your answer, the size of EACH of the
Calculate the size of EACH of the following following angles:
angles, giving reasons for your answers:
(a)  AOC
(a) VZW
(b)  ADC
(b) XYZ
11. In the diagram below, not drawn to scale, O 12. In the diagram below, not drawn to scale, O
is the centre of the circle,  AOB = 130°. is the centre of the circle ABCD and TEF is
a tangent to the circle at E.
 DAE = 30°, and AEC and BED are

chords of the circle. Given that DEF = 30º, calculate, giving
reasons to support your answer, the sizes of
(a) Calculate the size of EACH of the following the angles:
angles, giving reasons for EACH step of
your answers. (a) ACD
(b) EAD
(i)  ACB
(c) EOD
(ii)  CBD
(d) BCD
(iii)  AED
(b) Show that  BCE and  ADE are similar. 13. The diagram below, not drawn to scale,
shows a circle, centre O. BA is parallel to CD
(c) Given that CE = 6 cm, EA = 9.1 cm and and angle CBD = 45°.
DE = 5cm,
(i) calculate the length of EB
(ii) calculate correct to 1 decimal place

the area of  AED.
(a) Calculate, giving reasons, the values of x

and y.

(b) Show that ABCD is a square, giving the Calculate, giving reasons for your answers,
reasons for your answer. the sizes of the following angles:
(a)
14. In the diagram below, not drawn to scale, EDB
ABCT is a circle. AC and BT are diameters.
TP, the tangent at T, meets BA produced at (b) BEC
P, so that  APT = 40°.
(c) CBT
(d) BAE

RST and TQV are tangents to the circle
QSWXY. Angle RSW = 50°, angle STQ =
110°, and SW is parallel to QY.
Calculate, giving reasons for all statements,

the size of:
(a)
BTP
(b) BAT
(c) ABT
(d) ACT.
Calculate, giving reasons for your answers,
the sizes of angles:
ABT is a tangent to the circle BEDC, centre (a)
O. AEC is a straight line through the centre WQS
O, with angle ECB = 35°.
(b) WSQ
(c) WQY
(d) WXY.

(d) QPR
17. Given a circle, centre 0 and radius 5 cm.
Tangents QT and QS are drawn from a point 19. In the figure above, not drawn to scale, SR is
Q to touch the circle at T and at 5. Angle a tangent to the circle. The chords SN and
OQT = 35°. MP intersect at Q. The chord MQP
produced meets the tangent SR at R. Angle
The arc TS subtends the angle TRS at the SRP = 26°, angle QMS = 52° and angle PQS
circumference. = 76°.
Calculate the size of angle TRS.

(a) Calculate, giving reasons:
18. In the figure below, not drawn to scale,
PQR is a circle with centre, O. The angle (i) angle MSQ
PQO = 53°. PO is parallel to QR.
(ii) angle RSP
(iii) angle SPN.
(b) Given that SR = 12 cm, show that the area

of ∆ MRS = 39 cm2, correct to 2 significant
20. ABCT, inscribed in a circle. ED is a tangent

to the circle at T. Angle ATE = 70°, Angle
CTD = 40° and Angle TAB = 84°.
Calculate, giving reasons to support your

answers, the size, in degrees, of the angles:
(a)
POQ
(b) OQR
(c) PRQ

Calculate, giving reasons for your answers, the 22. In the diagram, A, B, C, D and E lie on a
magnitude of the angles: circle and EB = EC. The lines ED, AC and
(a) FB are parallel.
ABT
(b) BTC
(c) CDT.
21. In the diagram, AC is a diameter of the

circle ABCD. The straight lines EBA and
ECD cut the circle at A, B, C and D. AC and
BD cut at F. Angle BAC = 42° and angle
DAC = 31°.
Angle EBC = 75° and angle ACE = 20°.

Calculate:
(a) CED
(b) CDE
(c) ECD
(d) ACB
(e) ABF.
Calculate the angle
(a) BCD
(b) A CD
(c) ABF
(d) AFB
(e) AED.

Trigonometry II and Circle Theorem

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Trigonometry II and Circle Theorem

Uploaded by

Copyright:

Available Formats

CXC Mathematics General Proficiency Trigonometry II and Circle Theorem

Topics are object is 58.5 m away from the building on

1. angle of elevation / angle of depression

2. Circle Theorems 2. the angle of elevation of the line of sight of

Angle of Elevation / Angle of

An angle of elevation is always measured upwards

3. From the top of a vertical cliff 40 m high,

How far is the object from the base of the

Let x m be the distance of the object from the base of

1. A person stands at the window of a building

So, the object is 59.30 m from the base of the cliff.

4. A man who is 2 m tall stands on horizontal

Estimate the height of the tree.

Let the height of the tree be h. Sketch a diagram to

Calculating the length of the diagonal AP

Revision notes  Paper 2 Section II Page | 244

By Pythagoras' Theorem and triangle ACD,

Note that 3 figures are always given for bearings.

Calculating the angle between the diagonal AP and

So, the angle between the diagonal AP and the base

to find an angle, you can write as:

The Sine rule and the Cosine rules

The area of triangles without right angles can be computed by

to find an angle, you can write this as:

sin A sin B sin C

The sine rule can be applied when given:

two angles and one side, or,

two sides and one angle opposite to one of the

Revision notes  Paper 2 Section II Page | 246

BC = 12 cm,  BAC  30 and

(b) Calculating the area of Δ ABC

(b) the area of Δ ABC, Applying the formula:

(c) the value of the angle  . 1

(c) Calculating the value of the angle .

Revision notes  Paper 2 Section II Page | 247

2. the diagram below, not drawn to scale,

 PRQ = 43º Ans.

Solution: Applying sine rule:

Applying sine rule: 15.2  0.469 Working out to one

sin R sin 109

Revision notes  Paper 2 Section II Page | 248

(c) Calculating the area of Δ PQR With two sides and an

Applying the formula: 1

3. In the diagram below, not drawn to scale,

Applying sine rule:

c 2  400  225   600    0.342 

(a) Calculating the area of Δ ABC c 2  400  225  205.2 = 830.2

Revision notes  Paper 2 Section II Page | 249

AB = 28.8 km Ans. (c) F.

(c) Calculating the size of  CAB

A sketch (a) Calculating the size of angle D

400  830  225

4. A triangular sheet of cardboard, DEF, has

(b) Calculating the size of angle E

With three sides and

(a) D, Applying the cosine rule:

Revision notes  Paper 2 Section II Page | 250

2209  2809  961 Circle review

= 0.814 inversing Angles in an isosceles triangle

With two angles, the Angles in a transversal diagram

F  180   61.6  35.5  z = y

1. The angle at the centre and the angle at the

The angle at the centre is