Republic of the Philippines

ISABELA STATE UNIVERSITY

Echague, Isabela

COLLEGE OF ENGINEERING

CE 111 – CALCULUS 1

1. Chapter 6: THE DIFFERENTIAL

2. Overview/Introduction

- Differentials
- Approximate Formulas

3. Discontinuous Derivatives.Learning Outcome/Objective

At the end of the discussion, the student should be able to:

1. Understand the concept of derivatives and differentials;
2. Find the differential of a function; and;
3. Solve approximation problems using differentials.

4. Learning Content/Topic

I. DIFFERENTIALS

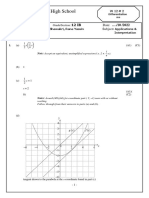
Consider an interval in which a curve relating 𝑥 and 𝑦 has a slope 𝑦’. Let 𝑃: (𝑥, 𝑦) be a
point on the curve, as shown in Figures 1 and 2. A change ∆𝑥 in the value of 𝑥 changes
y by some amount ∆𝑦. In the Figures 𝑃’ is the point (𝑥 + ∆𝑥, 𝑦 + ∆𝑦); ∆𝑦 is the distance
𝑄𝑃’. Unless the equation of the curve is particularly simple, it may be difficult to compute
∆𝑦. We seek for ∆𝑦 an approximation which must satisfy two requirements: First it must
be possible for us to prove that the difference between the approximation and ∆𝑦 can be
made arbitrarily small by taking ∆𝑥 sufficiently small; second, the approximation must be
easy to compute.

In Figure 1 and Figure 2, the tangent line at 𝑃 intersects the ordinate through 𝑃’ at the
point 𝑅. Examination of the figures shows that it is plausible that the length 𝑄𝑅 is an

Figure 1 Figure 2

1 |Calculus 1–Module 6: The Differential

 approximation to 𝑄𝑃’ = 𝛥𝑦 for small 𝛥𝑥. Let us see whether 𝑄𝑅 satisfies our two
requirements.
At 𝑃, the slope of the curve is . Now 𝑃𝑄 = ∆𝑥, so that we obtain
e
(𝟏) 𝑄𝑅 = 𝑦′∆𝑥

We already know how easy it is to compute the slope y’. Hence our second requirement
is satisfied by 𝑄𝑅.

The difference between 𝑄𝑅 and 𝑄𝑃’ is given by

𝑃 𝑅 = 𝑄𝑅 − 𝑄𝑃 = 𝑦 ∆𝑥 − ∆𝑦

Our first requirement demands that we show that 𝑃’𝑅 → 0 as ∆𝑥 → 0.

We shall do even better by showing that → 0 as ∆𝑥 → 0. Indeed,

∆
e
𝑃𝑅 ∆𝑦
(𝟐) Lim = Lim 𝑦 − =𝑦 −𝑦 =0
∆ → ∆𝑥 ∆ → ∆𝑥

because
∆𝑦
Lim = 𝑦′
∆ → ∆𝑥

since we are working in an interval where the slope exists. In a sense (2) shows that
𝑃’𝑅 → 0 more rapidly than ∆𝑥 → 0.

The quantity 𝑄𝑅 is called the differential of 𝑦 and is denoted by 𝑑𝑦.

By equation (1)

(𝟑) 𝑑𝑦 = 𝑦′∆𝑥

Theoretically, we are still at liberty to define dx – i.e., the differential of the independent
variable – in any way we please. But if in (3) we put

𝑦=𝑥 , 𝑦 =1
the result is

(𝟒) 𝑑𝑥 = ∆𝑥

Thus, in order to avoid conflict when (3) is applied to the function y=x, we adopt (4) as
our definition. That is, the differential of the independent variable is equal to the increment
of that variable.

We may therefore write

(𝟓) 𝑑𝑦 = 𝑦 𝑑𝑥 = 𝑦′∆𝑥

and state the definition as follows:

2 |Calculus 1–Module 6: The Differential

 The differential of any function is equal to its derivative multiplied by the differential of
the independent variable.
Example ().
𝑦 = 𝑥 − 2𝑥
𝑑𝑦 = 3𝑥 𝑑𝑥 − 2𝑑𝑥
Example ().
𝑧 −1
𝑦=
𝑧 +1
(𝑧 + 1)2𝑧 𝑑𝑧 − (𝑧 − 1)2𝑧 𝑑𝑧
𝑑𝑦 =
(𝑧 + 1)
4𝑧𝑑𝑧
=
(𝑧 + 1)
Example ().
𝑦 + 2𝑥𝑦 = 3
3𝑦 𝑑𝑦 + 2𝑥 𝑑𝑦 + 2𝑦 𝑑𝑥 = 0
2𝑦𝑑𝑥
𝑑𝑦 = −
3𝑦 + 2𝑥

Here we have an excellent example in support of the statement made in the first
paragraph of this chapter to the effect that it may be difficult to compute ∆𝑦. From

𝑦 + 2𝑥𝑦 = 3
and
(𝑦 + ∆𝑦) + 2(𝑥 + ∆𝑥)(𝑦 + ∆𝑦) = 3

It follows rapidly that

(∆𝑦) + 3𝑦(∆𝑦) + (3𝑦 + 2𝑥 + 2 ∆𝑥)(∆𝑦) + 2𝑦 ∆𝑥 = 0

The determination of ∆𝑦 from the above cubic is surely not simple compared with the
determination of 𝑑𝑦 as accomplished at the beginning of this example.

We see now that the technique of differentiation is the same, except for a slight change
in form, whether derivatives or differentials are used. It follows that differentials would
hardly be worth bothering with, if they were to be used merely as an additional tool in
differentiation.

II. APPROXIMATE FORMULAS

Very often we wish to compute, or to estimate within safe limits, the change in the value
of a function caused by a small change in the value of the independent variable. When
∆𝑥 is small, 𝑑𝑦 and ∆𝑦 are, in general, nearly equal, and in many cases the value of 𝑑𝑦
furnishes a sufficiently good approximation to the value of ∆𝑦.

In any approximate computation, the amount by which the computed value of the function
differs from the true value is called the error of the computation. Of course, in using any
approximate formula, we should make sure that the error committed is within the
allowable limit of error for the problem in hand.

Example (). Find an approximate formula for the area of a narrow circular ring.
The area of a circle of radius 𝑟 is

3 |Calculus 1–Module 6: The Differential

 𝐴 = 𝜋𝑟

When the radius increases by an amount ∆𝑟, the area increases by an amount ∆𝐴 which
is approximated by
𝑑𝐴 = 2𝜋𝑟 𝑑𝑟 = 2𝜋𝑟 ∆𝑟

(Since 𝑟 is the independent variable, 𝑑𝑟 = ∆𝑟.) Hence the area of a narrow circular ring
is approximately the product of the circumference by the width.

Example (). Find an approximate value for √8.73

Put 𝑦 = √𝑥, from which

𝑑𝑥
(𝟏) 𝑑𝑦 =
2√𝑥

For 𝑥 we choose a number which is close to 8.73 and for which we know the square root.
Choose

𝑥=9 𝑎𝑛𝑑 ∆𝑥 = 𝑑𝑥 = −0.27

So that 𝑥 + 𝑑𝑥 = 8.73. From (1) it follows that

0.27 0.27
𝑑𝑦 = − =− = −0.045
2√9 6
Then
√8.73 = 𝑦 + 𝑑𝑦 = 3 − 0.045 = 2.955

approximately. To five decimal places the correct value is 2.95466.

5. Teaching and Learning Activities

EXERCISES
1. 𝑦 = 3𝑥 − 5𝑥 + 𝑥 − 4 16. 𝑥 = 𝑦 (9 − 𝑦 )
2. 𝑧 = (1 − 2𝑣 + 𝑣 ) 17. 𝑟 =
√
3. 𝑥 = (5𝑡 − 2) √
4. 𝑦 = (1 − 𝑥 ) 18. 𝑟 =
5. 𝑧 = √4 − 3𝑥 19. 𝑦 = 1 + √𝑥
6. 𝛽= 20. 𝑦 = 1 + √𝑥
√
7. 𝑢 = 2𝑦 − 𝑦 21. 𝑥 =
( )
8. 𝑥 = 𝑡 − √𝑡 + ( )
22. 𝑦 = ( )
9. 𝑦 = 𝑥(3 + 2𝑥)
–
10. 𝑤 = 𝑥 (1 − 𝑥 ) 23. 𝑟 =
11. 𝑢 =
24. 𝑦 =
12. 𝑥 = 25. 𝑦 = 4𝑎𝑥
√
13. 𝑦 = √𝑥 − 𝑎 , 𝑎 held constant. 26. − =1
14. 𝑦 = √𝑥 − 𝑎 , 𝑥 held constant. 27. 𝑥 + 𝑥𝑦 + 𝑦 = 4
15. 𝑥 = 𝑡 (𝑡 + 4) 28. 3𝑥 − 6𝑥𝑦 + 3𝑦 − 7𝑥 + 2𝑦 − 1 = 0

4 |Calculus 1–Module 6: The Differential

 29. 𝑦 = 31. 𝑦 =
30. 𝑦 = 32. 𝑥 + 𝑦 − 3𝑎𝑥𝑦 = 0
33. Find approximately the volume of a thin spherical shell.
34. Find an approximate formula for the volume of a thin cylindrical shell of given height.
35. Find approximately the volume of wood required to make a cubical box, of edge
length 6ft., using boards ½ in. thick.
36. The base of a right triangle is fixed at 3 ft., the hypothenuse is 5 ft. long and subject
to change. Find the approximate change in altitude when the hypothenuse is changed
by a small amount ∆ℎ.
37. The diameter of a circle is measured and found to be 6 ft. with a maximum error of
0.1 in. Find the approximate maximum error in the computed area.
38. The diameter of a sphere is measured and found to be 3 ft. with a maximum error of
0.1 in. Find the approximate maximum error in the computed volume.
39. The diameter of a circle is to be measured, and its volume computed. If the diameter
can be measured with a maximum error of 0.001 in., and the area must be accurate
to within 0.1 sq. in., find the largest diameter for which the process can be used.
40. The diameter of a sphere is to be measured, and its volume computed. If the diameter
can be measured with a maximum error of 0.001 in., and the volume must be accurate
to within 0.1 cu. in., find the largest diameter for which the process can be used.
41. Find approximately the change in the reciprocal of a number 𝑥 produced by a small
change in the number. Investigate also the case when the number itself is small.
42. The volume of a body of gas is measured; the pressure is then computed from the
formula
𝑘
𝑝=
𝑣

If the allowable error in 𝑝 is 0.001𝑘, and the maximum error in measuring 𝑣 is 0.6 cu.
ft., what is the volume of the smallest container to which the process can be applied?

In the following exercises, use differentials to approximate to the desired number.

43. The square root of 627. 49. The cube root of 26.
44. The square root of 398. 50. The cube root of 0.009.
45. The square root of 193. 51. The cube root of 1.35.
46. The square root of 287. 52. The cube root of 3.3.
47. The square root of 0.253. 53. The fourth root of 17.
48. The square root of 98.8. 54. The fourth root of 255.

6. Flexible Teaching Learning Modality (FTLM) adapted

Module, Messenger Rooms/ Google Classroom / Google docs

Exercises and Problem Sets.

7. Assessment Task

Assessment Task will be a 30-point quiz covering the topics discussed in this module.
In addition, a long exam will be given at the end of the term

5 |Calculus 1–Module 6: The Differential

8. References (Copyrighted within the last 10 years)

This contains the list of references/readings which students can explore.

Love, C.E. Ph.D, Rainville E.D. Ph.D. 1981. Differential and Integral Calculus.
MACMILLAN PUBLISHING CO., INC.

Peterson, T.S. Calculus with Analytic Geometry. Ken Incorporated, Quezon City

6 |Calculus 1–Module 6: The Differential