Republic of the Philippines

ISABELA STATE UNIVERSITY

Echague, Isabela

COLLEGE OF ENGINEERING

CE 111 – CALCULUS 1

1. Chapter 2: Derivative, Slope and Rates of Change

2. Overview/Introduction

- The Derivative
- Determination of the Derivative
- Tangents to Plane Curves
- Derivative Interpreted as Slope
- Rate of Change

3. Learning Outcome/Objective

At the end of the discussion, the student should be able to:

1. Understand the concept of the derivative;

2. Find the derivative of any function;
3. Determine the slope/s of a function;
4. Analyze and solve problems on Rates of Change.

4. Learning Content/Topic

I. THE DERIVATIVE

Given a continuous function

𝑦 = 𝑓(𝑥)
let us choose some fixed value of 𝑥, the corresponding value of 𝑦 being given the
function 𝑦 = 𝑓(𝑥). Now consider another value of 𝑥, differing from the first one by
an amount (positive or negative) which we will call the increment of 𝒙, and will
denote by the symbol ∆𝑥. For this value of 𝑥, 𝑦 will have a new value, differing
from the original by an amount of ∆𝑦. In other words, when 𝒙 changes to the
value, 𝒙 + ∆𝒙, 𝒚 changes to the value 𝒚 + ∆𝒚, and we have

𝑦 + ∆𝑦 = 𝑓(𝑥 + ∆𝑥)
∆𝑦 = 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥)
∆
Now let us form the ratio , and investigate the behavior of this ratio when ∆𝑥
∆
approaches zero. Since f(x) is continuous, the ∆𝑦 of the equation above also
approaches zero. We have found that when both numerator and denominator of
a fraction approach zero, the fraction itself may, or may not, approach a limit. In

1 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change

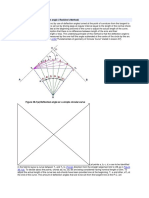
 Figure 1, let the curve AB represent the
∆
graph of the given function. The ratio is
∆
the slope of the line joining the points
𝑃: (𝑥, 𝑦) and 𝑃 : (𝑥 + ∆𝑥, 𝑦 + ∆𝑦). As ∆𝑥
approaches zero, 𝑃′ approaches 𝑃 along
the curve, and in all ordinary cases the line
𝑃𝑃’ approaches a certain straight line (PT
in the Figure 1) as a limiting position. That
is, for a sufficiently well-behaved curve, the
∆
ratio approaches a limit, the slope of the
∆ Figure 1
𝑃𝑇.

The limit is called the Derivative of 𝒚 with respect to 𝒙.

FUNDAMENTAL DEFINITION: The derivative of y with respect to x is the limit of

∆
the ratio when ∆𝑥 approaches zero.
∆

The derivative is designated by the symbol:

𝑑𝑦 ∆𝑦 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥)
= Lim = Lim
𝑑𝑥 ∆ → ∆𝑥 ∆ → ∆𝑥
Other symbols for the derivative are 𝑦 , 𝑓 (𝑥), 𝐷 𝑦, 𝑓(𝑥). But since the symbol
y’ does not explicitly indicate the independent variable, this notation should be
used only when no confusion or ambiguity can arise.

The operation of finding the derivative is called Differentiation. Only

differentiable functions (those having a derivative)

II. DETERMINATION OF THE DERIVATIVE

Our first problem is to prove, for the elementary functions, the existence of the
∆
derivative – i.e., to prove that when ∆𝑥 approaches zero, approaches a definite
∆
limit – and at the same time to derive formulas for the derivative in terms of 𝑥, for
the various functions.

To obtain the derivative of any function, the general process is as follows:

1. Replace 𝑥 by 𝑥 + ∆𝑥, and 𝑦 by 𝑦 + ∆𝑦:

𝑦 = 𝑓(𝑥) (𝟏)
𝑦 + ∆𝑦 = 𝑓(𝑥 + ∆𝑥) (𝟐)

2 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change

 2. By subtraction, eliminate 𝑦 between (1) and (2), thus obtaining a formula for
∆𝑦 in terms of 𝑥 and ∆𝑥:

∆𝑦 = 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) (𝟑)

3. By some suitable transformation, throw the right member of (3) in to a form

which contains ∆𝑥 explicitly as a factor.

4. Divide through by ∆𝑥:

∆𝑦 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥)
=
∆𝑥 ∆𝑥

5. Determine the limit as ∆𝑥 approaches zero.

The transformation required in step 3 varies with different classes of functions

and must be discovered by trial. For transcendental functions, evaluation of the
limit in the final step is not always a simple problem. We shall see how to
overcome these difficulties as the arise.

Example (). Differentiate the function 𝑦 = 𝑥 − 2𝑥

1. 𝑦 + ∆𝑦 = (𝑥 + ∆𝑥) − 2(𝑥 + ∆𝑥)

2. ∆𝑦 = (𝑥 + ∆𝑥) − 2(𝑥 + ∆𝑥) −(𝑥 − 2𝑥)
3. ∆𝑦 = 𝑥 + 3𝑥 ∆𝑥 + 3𝑥(∆𝑥) + ∆𝑥 − 2𝑥 − 2∆𝑥 − 𝑥 + 2𝑥
∆𝑦 = 3𝑥 ∆𝑥 + 3𝑥(∆𝑥) + ∆𝑥 − 2∆𝑥
∆
4. = 3𝑥 + 3𝑥∆𝑥 + (∆𝑥) − 2
∆
5. 𝒚 = 𝟑𝒙𝟐 − 𝟐

Example (). Find the derivative of the function 𝑥 =

1. 𝑥 + ∆𝑥 =
∆
2. ∆𝑥 = −
∆
( ∆ ) ∆
3. ∆𝑥 =
(
=(
∆ ) ∆ )
∆
4. =(
∆ ∆ )
5. =−
III. TANGENTS TO PLANE CURVES

A straight line that intersects a curve in two or more distinct points is called a
secant.

3 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change

 Let 𝑃 be a fixed point of a plane curve,
and 𝑃’ a neighboring point. If 𝑃’ be
made to approach 𝑃 along the curve,
the secant 𝑃𝑃’ approaches, in general,
a definite limiting position, 𝑃𝑇 in Figure
2. If the secant line has such a limiting
position, then the straight line which is
that limit, 𝑃𝑇 in Figure 2 is called the
tangent to the curve at 𝑃, or is said to
touch the curve at 𝑃. The point 𝑃 is the
point of contact.
Figure 2

The slope of the tangent to the curve at any point is called simply the slope of the
curve at that point. When 𝑃’ approaches 𝑃, the slope of the secant approaches
as its limit the slope of the curve.

IV. DERIVATIVE INTERPRETED AS SLOPE

∆
In Figure 1, the slope of the secant 𝑃𝑃’ is . As ∆𝑥 approaches zero, 𝑃’
∆
approaches 𝑃 along the curve, so that the slope of the secant approaches as its
limit the slope of the curve at 𝑃. But this limit has been defined as the derivative
of 𝑦 with respect to 𝑥. The derivative of a function is identical with the slope of the
graph of the function.

More explicitly, this means that if, in the formula for 𝑦’ we substitute any given
value of 𝑥, the number thus obtained is the slope of the curve at the point whose
abscissa is the given 𝑥.

Example (). Find the slope of the curve 𝑦 = 𝑥 − 2𝑥 at the point 𝑃: (2, −2)

𝑦 = 𝑥 −2
when 𝑥 = 2, this takes the value

𝑦 =1
which is the slope at the given point (slope of
the tangent 𝑃𝑇 in Figure 3).

Let us verify that the term “slope of a curve” does

not conflict with the previously used term “slope of
a line”.
Figure 3

4 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change

 The equation of a line of slope m can be written

(1) 𝑦 =𝑚𝑥+𝑏
From it we obtain:

𝑦 + ∆𝑦 = 𝑚(𝑥 + ∆𝑥) + 𝑏
∆𝑦 = 𝑚∆𝑥
∆𝑦
=𝑚
∆𝑥
Hence, for the straight line (1),
𝑑𝑦
=𝑚
𝑑𝑥
The two uses of the word “slope” are in agreement.

V. RATE OF CHANGE

The idea of rate of change of a function occurs constantly in everyday experience.

Such familiar expressions as miles per hour, miles per gallon, pressure per
square inch, value per acre, price per ton, all represent rates.

Given a function
𝑦 = 𝑓(𝑥)
Let us assign to 𝑥 an arbitrary increment ∆𝑥, thus causing in 𝑦 a (positive or
∆
negative) change ∆𝑦. The ratio is called the average rate of change over the
∆
interval ∆𝑥. If we let ∆𝑥 approach zero, this ratio in general approaches a limiting
value, which is defined as the rate of change of 𝑦 corresponding to the given value
of 𝑥, or the instantaneous rate:
𝑑𝑦 ∆𝑦
= Lim = 𝑟𝑎𝑡𝑒 𝑜𝑓 𝑐ℎ𝑎𝑛𝑔𝑒 𝑜𝑓 𝑦 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑥.
𝑑𝑥 ∆ → ∆𝑥

In order to understand and appreciate these ideas, nothing more than ordinary
experience is needed. As an illustration, suppose that two posts, at a measured
distance apart, are set up beside a highway, and that a car is driven past them.
Let ∆𝑥 be the distance between the posts, and ∆𝑡 the time required to pass. Then,
∆
if the car travels at a uniform speed, that speed is merely . But if the speed is
∆
a variable, this ratio is the average speed. If we wish to know the speed at a
particular instant, say, when passing the first post, common sense would suggest
that the posts be placed close together. For then ∆𝑥 will be small, and there will
not be time for the speed to change a great deal, so that the average will be nearly
equal to the instantaneous speed. While in practice this process could not be

5 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change

 pushed beyond a certain point, our ordinary idea of instantaneous speed is
∆
expressed exactly by , the limit of as ∆𝑡 approaches zero.
∆

Comparing the definitions of derivative and rate of change, we have another

fundamental relation: The derivative of a function is identical with its rate of
change.

Thus, in our future work it must always be borne

in mind that the three quantities – derivative,
slope of graph, rate of change – are all equal to
each other.

When the slope of a curve is positive (as on the

𝑎𝑟𝑐 𝐴𝐵), the ordinate 𝑦 is increasing (as 𝑥
increases). When the slope is negative (as on
𝐵𝐶), the ordinate is decreasing. This says that a
function increases or decreases according as its Figure 4
rate of change is positive or negative.

Example (). Find the rate at which the reciprocal of a number changes as the
number increases.
Let 𝑛 equal the number, 𝑟 its reciprocal.
1
𝑟=
𝑛
Getting the derivative, we find
𝑑𝑟 1
=−
𝑑𝑛 𝑛

At the instant, say, when n passes through the value 2, the reciprocal is
diminishing one-fourth as fast as the number is increasing.
Example (). The surface area of a sphere, initially zero, increases uniformly at
the rate of 4 sq. in. per sec. Find the rate at which the radius is increasing at the
end of 2 sec.

Let: 𝑡 = 𝑡𝑖𝑚𝑒 (𝑠𝑒𝑐. )

𝑟 = 𝑟𝑎𝑑𝑖𝑢𝑠 𝑜𝑓 𝑠𝑝ℎ𝑒𝑟𝑒 (𝑖𝑛. )
𝑆 = 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝑎𝑟𝑒𝑎 (𝑠𝑞. 𝑖𝑛. )

Since 𝑆 is increasing at a constant rate, 𝑆 is proportional to the elapsed time;

indeed,

𝑆 = 4𝑡
But also, 𝑆 = 4 𝜋 𝑟 , so that 4𝑡 = 4 𝜋 𝑟 , from which it follows that

6 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change

 √𝑡
𝑟=
√𝜋
By differentiating, we find
𝑑𝑟 1
=
𝑑𝑡 2√𝜋 ∙ √𝑡
When 𝑡 = 2,

𝑑𝑟 1
= = 𝟎. 𝟐 𝒊𝒏. 𝒑𝒆𝒓 𝒔𝒆𝒄.
𝑑𝑡 2√2𝜋

It contains readings, selection and discussion questions and sets of activities

that students can work on individually or by group.

5. Teaching and Learning Activities

Exercises
Differentiate the following functions:
1. 𝑦 = 4𝑥 − 3𝑥 − 2
14. 𝑦 =
2. 𝑦 = 3 + 4𝑥 − 𝑥
3. 𝑦 = 𝑥 − 5𝑥 + 2 15. 𝑥 =
4. 𝑦 = 𝑥 − 2𝑥 + 6
5. 𝑥 = 𝑦 − 2𝑦 16. 𝑣 =

6. 𝑥 = 𝑡 − 5𝑡 − 3 17. 𝑦 = √𝑥 + 2

7. 𝑦 = (3𝑥 + 1) 18. 𝑦 = √2 − 3𝑥

8. 𝑦 = (𝑥 − 2) 19. 𝑦 = √𝑎 + 𝑥
20. 𝑣 = 𝑎 −𝑦
9. 𝑦 =
21. 𝑦 = 3𝑥 − √𝑥
10. 𝑥 = 22. 𝑥 = 3𝑡 − 2√𝑡

23. 𝑦 =
11. 𝑥 = √

12. 𝑥 =
24. 𝑢=𝑡

25. 𝑦 =
13. 𝑦 = 2 − 3𝑥 − √
26. 𝑦 = 𝑥√𝑥 − 1

7 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change

 27. For the function 𝑦 = √2 − 3𝑥, show that the derivative does not exist at 𝑥 = .

28. For the function 𝑢 = 𝑡 , show that the derivative does not exist at 𝑡 = 0 but that
the right-hand derivative exists at that point.
29. 𝑦 = cos 𝑥 32. 𝑦 = csc 𝑥
30. 𝑦 = tan 𝑥 33. 𝑦 = sec 𝑥
31. 𝑦 = cot 𝑥
For the following functions, find the slope of the curve at the given point.
34. 𝑦 = 2 − 𝑥 , (3, −7)
39. 𝑦 = , (−2 , −1)
35. 𝑦 = 3𝑥 − 2𝑥 , (2, 8)
40. 𝑦 = 4𝑥 , (1 , 2)
36. 𝑦 = 2𝑥 − 3𝑥 , (−1, 1)
37. 𝑦 = 𝑥 − 𝑥 , (1, 0) 41. 𝑦 = 4𝑥 , (1 , −2)
42. 𝑦 = 3𝑥 + 1 , (1 , 2)
38. 𝑦 = , (2, )
43. 𝑦 = 3𝑥 + 1 , (− , 0)

44. Find how fast the (a) circumference, (b) the area, of a circle increases when the
radius increases.
45. Find how fast (a) the volume, (b) the surface area, (c) the diagonal, of a cube
increases when the length of the edge increases.
46. Find how fast (a) the volume, (b) the surface area, of a sphere increases as the
radius increases.
47. The radius of a sphere, initially zero, increases at the rate of 6 ft per second.
How fast the volume is increasing after ¼ second.
48. A right circular cylinder has a fixed height of 6 units. Find the rate of change of
its volume 𝑉 with respect to the radius 𝑟 of its base.
49. In 48, find the rate of change of the total surface area 𝐴 with respect to 𝑟.
50. The dimensions of a box are 𝑏, 𝑏 + 1, 𝑏 + 4. Find how fast the total surface area
𝐴 increases as 𝑏 increases.
51. For the previous example, find how fast the volume increases as 𝑏 increases.

This is a list of concepts and thinking skills that were covered in the module.
It also includes questions or an activity that integrates the idea, help learners to
connect to the module question, assess progress, and look ahead. Likewise, this

8 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change

 may contain additional problems that could be used for homework or tests, or
additional readings that allow students to apply new knowledge and skills in a
different context

6. Flexible Teaching Learning Modality (FTLM) adapted

Module, Messenger Rooms/ Google Classroom

Exercises and Problem Sets.

7. Assessment Task

Assessment Task will be a 30-point quiz covering the topics discussed in this module.
In addition, a long exam will be given at the end of the term

8. References (Copyrighted within the last 10 years)

This contains the list of references/readings which students can explore.

Love, C.E. Ph.D, Rainville E.D. Ph.D. 1981. Differential and Integral Calculus.
MACMILLAN PUBLISHING CO., INC.

Peterson, T.S. Calculus with Analytic Geometry. Ken Incorporated, Quezon City

9 |Calculus 1 – Module 2: Derivative, Slope & Rates of Change