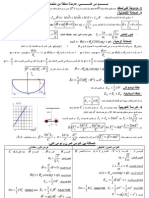
CHAPTER 5 - OPERATIONAL AMPLIFIER List of topics for this chapter : Operational Amplifiers Ideal Operational Amplifier Inverting Amplifier Noninverting Amplifier Summing Amplifier Difference Amplifier Cascaded Operational Amplifier Circuits Operational Amplifier Circuits with PSpice Applications ——————————————xqxqo OPERATIONAL AMPLIFIERS, ProblemS.1 Calculate V,y for Ry, = 12, 100 2, 1 kQ, 10k, 100 kA, given the 2kQ = ee circuit in Figure 5.1. Figure 5.1 > Carefully DEFINE the problem. Each component is labeled completely. The problem is clear. > PRESENT everything you know about the problem. ‘The value of the load resistor, R,,, is varied over a wide range of values. The dependent voltage source (a valtage-controlled voltage source) has a large gain (100k). Obviously, the goal of the problem is to determine the output voltage in terms of the input (or source) voltage. > Establish a set of ALTERNATIVE solutions and determine the one that promises the e@ greatest likelihood of success. 1v ‘Vi can be determined using nodal analysis, mesh analysis, or circuit analysis, Because we want to find a voltage, rather than a current, we will use nodal analysis, ATTEMPT a problem solution, Use nodal analysis to find V,y in terms of V, and Ry, At the left node or Vi, 100k Atthe right node or Vig, 2 Vou -Vin . Vou + 100K V, ° 2% 50 ‘Simplifying the left node equation, 00)(Viq — V,) + Vin + SON(Vig = Vout) = 0 151V,, ~100V, -50V yy = 0 Simplifying the right node equation, 2k (Vea = Van) + (40)(Vg +100K Vig) + Van = 0 1 (a1 x). +(4M-DV, Ru 2k {a+25) 4M-1°™ Substituting the simplified right node equation into the simplified left node equation, 2k -asi{aie 2] Gar Vou 100V, ~ 50 Vag 2k -asn{sie2 J-csoxan—n aM oD Vow = 100V, (100)(4M_ iw at Substitute each value for R,, into this equation to find V,,, in terms of V, For R, =19, Vou = ~1.99692283 V, BFor R, =1002, — Vyy = -1.99990789V, For Ry, =1kQ, Vig. = -1.99993507V, For Ry =10kKQ, Vig = -1.99993779V, For R, =100kQ, — V,, = -1.99993806V, ' > EVALUATE the solution and cheek for accuracy. First, the answers appear reasonable with the gain of the entire circuit approaching 2 as Ry increases in size. In addition, even for R, = 1.2, Vjq =2V, is a good approximation Clearly, using an ideal op amp is reasonable. > Has the problem been solved SATISFACTORILY? Ifo, present the solution; if not, then return to “ALTERNATIVE sol ns” and continue through the process again. This problem has been solved satisfactorily. For R, =19, Ve = ~1.99692283 V, For R, =1002, Vi = ~1,99990789V, For Ry =1kQ, Voy, = -1.99993507 V, For Ry =10kQ, Vy = =1.99993779V. For R, =100KQ, Vy, = =1.99993806V, Problem 5.2 ' Determine: (a) () (©) [5.1] The equivalent model of a certain op amp is shown in Figure 5.2. the input resistance, the output resistance, the voltage gain in dB. a 9Ay = 201og,9(8%10") Ay = 98.06 e Problem 5.3 Solve for V,, whenR, = 1.0, 1kQ, 100 KO, 1 MQ, given the cireuit in Figure 5.3. 1kQ = —W— 502 * 7 Vou = Ri Vs Vin S 1000 100k Vin - . Figure 5.3 Use nodal analysis to find V,,, in terms of Vs and R,, Atthe left node or Vi, : Ma=Vs , Vin Via = Vs, Vin =0 Ik 100k Atthe right node or Vay: Vou +100K Vi, Vay 0 50 R, ‘Simplifying the left nodal equation, (100)(V, - Vs) + Vi, =0 101V, =100V, 1, = Oy, 101 Vou +2K Vig Simplifying the right node equation, (2% SOR, 100KR, Ve -( 50 in = 2k Vig 80Substituting the simplified left node equation into the simplified right node equation, e v (eee | (, -10MR,, y on “UR, 50 Mor "s “(a one, +50)" Substitute each value for Rj, into this equation to find V,,,, in terms of Vs For R, =1Q, For Ry =1kQ, -94,295.1438 V, For R, =100 kQ, ~98,960.4208 V, For Ry =1MQ, Vey = -99,004.9507V, = + IDEAL OPERATIONAL AMPLIFIER ‘An ideal op amp has infinite open-loop gain, infinite input resistance, and zero output resistance. Problem 5.4 Looking at the circuit in Figure 5.4, what effect docs R,, have on the value e Figure 5.4 > Carefully DEFINE the problem. Each component is labeled completely. The problem is clear. > PRESENT everything you know about the problem. Essentially, we are to determine if the value of R,, affects the output voltage in any way. ‘Thus, the goal of the problem is to solve for V, in terms of the other variables. 81‘Treat the operational amplifier as ideal. Due to infinite input resistance, we know that the currents into both input terminals are zero. The voltage across the terminals is negligibly e. small or V, = Vy. Establish a set of ALTERNATIVE solutions and determine the one that promises the greatest likelihood of suecess. Because this is a circuit problem, we can use nodal analysis, mesh analysis, or basic circuit analysis. Nodal analysis typically works best for op amp circuits. ATTEMPT a problem solution. Referring to the circuit below, there are three unknown nodes. Rr Write a node equation at node a. The node voltage at node b is already known, V, = 0 e Writing a node equation at node ¢ will only introduce an additional unknown. This gives two equations with four unknowns. Solving for V, in terms of V, (and the resistances) implies that we need one equation with two unknowns. Hence, we need a constraint equation to reduce the number of unknowns. v,-V,. V.-¥. At node a, At node b, ‘The constraint equation comes from a characteristic of the ideal op amp. Vi=Me Thus, = V,=V,=0 ‘Substitute the constraint into the node equation for node a to solve for V, .Hence, Clearly, We have shown that the value of R,, has no effect on the value of V,, assuming that Ry. is finite and not equal to zero. EVALUATE the solution and check for accuracy. Consider the following circuit. 1 R& ws + Vs Using Ohm's law, T From a characteristic of the ideal op amp, V, = V, But v,=0 —> v,=0 Also, But So, Thus, 83(Our check for accuracy was successful > Has the problem been solved SATISFACTORILY? If so, present the solution; if not, then return to “ALTERNATIVE solutions” and continue through the process again. This problem has been solved satisfactorily. ‘The value of Ry has no effect on the value of V,, assuming that Ry is finite and not zero. 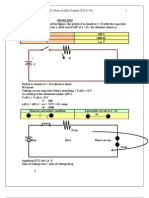Problem 5.5 [5.11] Find v, and i, in the circuit in Figure 5.5. 2kQ 8kQ AW AW Ve . 5kQ i AW 3V Atnodeb, — ¥, -( At node a, ).5m— 0.5m, 84INVERTING AMPLIFIER ‘An inverting amplifier reverses the polarity of the input signal while amplifying it. Problem 5.6 [5.19] __Using the circuit in Figure 5.6, calculate v, if v, = 0. 8kQ Pt ov Vo At node a, a At node b, Q) Hence, (2) becomes and (1) becomes 85Problem 7 Express V, inerms of V, forthe circuit shown in Figure 5.7 e Ri Vs AM - Vs pI + Figure 5.7 Using nodal analysis, NONINVERTING AMPLIFIER Problem 5.8 How does the circuit in Figure 5.8 differ from the circuit in Figure 5.4? Figure 58 86Using nodal analysis, where V, = V, = V, is the constraint equation Simplifying, between the output styakaee 'V,.and the input voltage, V..is a simple ratio of Ry and Rj. For the circuit in Figure 5.8, however. the gain can never be less than one. Since there is rarely ‘case where the gain is less than one, this is not normally a problem. aS SUMMING AMPLIFIER A summing amplifier combines several inputs and produces an output that is the weighted sum of the inputs. Problem 5.9 [5.33] __A four-input summing amplifier has R, = R, =R, = Ry = 12 KQ. What value of feedback resistor is needed to make it an averaging amplifier? Re) Re Re Aty, + Sty, + Sty, + Se RR, Ry) Ry 12k el 1 Re Oe) ee a aoe In order for SH(y, +¥) +V3 +¥4) to become 87Problem 5.10 ‘What have we done here? Express Vy in terms of V, and V, for the circuit shown in Figure 5.9. 10kQ 10kQ ~ AW Wy vy * vs + V2 Figure 5.9 Using nodal analysis, V.-V..Y-% Y-V, M=VM=V2 Va Veu 29 10k 10k 10k where V, = V, = 0 is the constraint equation 2M Ve Vou 10k * 10k * 10k We have constructed an inverting, summing amplifier. + DIFFERENCE AMPLIFIER A difference amplifier amplifies the difference between two inputs but rejects any signals common to the two inputs. Problem 5.11 Vou = V2 - Vy? Yes, we want to construct what is called a difference amj shown in Figure 5.10. 88. Using an operational amplifier, can we construct a cireuit where We can do this using the circuitFigure 5.10 ‘Now, verify that this circuit will amplify the difference of the two inputs. Using nodal analysis, v-¥,, Vou 9 and where V, = V, is the constraint equation Simplifying, 1fR, =R, and Rs = Ra, ‘MM This was the desired case. 89Problem 5.12 5.39] __ Design a difference amplifier to have a gain of 2 and a common mode input resistance of 10 kQ at each input. ‘The input resistances are R, =R,=10kQ For a gain of 2, =2=2 —» R,=2R,=20kQ ‘A property of difference amplifiers is Ri _Ry Thus, ‘Now, verify the results, R, (+R,/R;) R, (RR) (7 tan) 20k Ye =o Ai0.5)%*~ 10k ** v, =2(¥3-¥)) This is the desired result. Therefore, R, =R, =10kQ R, CASCADED OPERATIONAL AMPLIFIER CIRCUITS ‘A cascade connection is a head-to-tail arrangement of two or more op amp circuits such that the output of one op amp circuit is the input to the next op amp circuit. Problem 5.13 [5.45] __Referto the oirouit in Figure 5.11. Calculate i, if @ — v,=12mV (6) v, = 10c0s(377t) mV 90pa 12kQ 6kQ eee Figure 5.11 ‘This is a cascading system of two inverting amplifiers. (Zz 6y, Ys =3x10° 2x1 Ye (a) ‘When V, 2mV, 36 A (&) When v, = 10c0s(377t) mV 30c0s(377t) HA OPERATIONAL AMPLIFIER CIRCUITS WITH PSPICE Problem 5.14 Solve Problem 5.1 us 1g PSpice. PSpice does not perform symbolic simulations. So, let V,=1V. Adda VIEWPOINT to the circuit to indicate the output voltage. Set the load resistor to the desired value, save the schematic and simulate. With the repetition of setting the load resistor and simulating the circuit, the output voltage for each load resistor in Problem 5.1 can be verified. 91R2 -1,.99692283V Rt ca ie P4550 GaIN=t00k} RS E R35 100k . EI l From the schematic, for R, =12, Vou = -1.99692283 V By changing the load resistor and simulating the circuit, it can be shown that for R, =1002, 1,99990789 V for R, =1kQ, -99993507 V for R, =10kQ, 99993779 V for R, =100kQ, ‘This matches the answers obtained in Problem 5.1 when V, Problem S.15 Solve Problem 5.7 using PSpice. Consider the following schematic, 92Because PSpice does not perform symbolic simulations, let V, =1V. We also need to choose values for the resistors. For the circuit above, let v,=1V, R, which produces, ‘This verifies the answer obtained in Problem 5.7. One must realize that Problem 5.7 was performed assuming an ideal op amp; PSpice does not simulate an ideal op amp. Thus, the output voltage may not be an integer value even though the calculations from Problem 5.7 would predict an integer value. Also, the output voltage cannot be greater than V+ or less than V-, where V+ and V— are the power supply voltages of the op amp. ‘There are three modes in which real op amps can operate. The most desirable is to have them give the desired output. The second mode is when the op amp goes into saturation, reaching its ‘maximum output voltage and remaining there. ‘The third mode is that the op amp can act like an oscillator; its output voltage can be some type of periodic signal such as a sine wave. Problem 5.16 Solve Problem 5.8 using PSpice. Consider the following schematic. R2 10k 33For the circuit above, V,=1V, R,)=1kQ, and and Re aoe = Vv, -(Reupy, (e sjo-u v This verifies the answer obtained in Problem 5.8 Aso, see the comments made concerning ideal versus real op amps in Problem 5.15. eee APPLICATIONS Problem 5.17 Use an operational amplifier to change an ideal voltage source to an ideal current souree. Consider the following circuit. : 2 i at Lo aOR WwW PSL ‘a Vout Clearly, “ee In the circuit above, the op amp will maintain the current through the black box in the feedback path at i, Thus, the op amp is working like an ideal current source. 94