Plane and Solid Geometry Formulas Prepared by: RTFVerterra

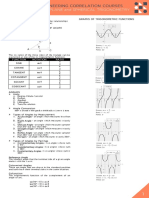
ASIAN Given four sides a, b, c, d, and sum of

two opposite angles:
10 sides
11 sides
=
=
decagon
undecagon
RADIUS OF CIRCLES
DEVELOPMENT 12 sides = dodecagon Circle circumscribed about a triangle
FOUNDATION A= (s − a)(s − b)(s − c)(s − d) − abcdcos2 θ 15 sides = quindecagon (Cicumcircle)
16 sides = hexadecagon
COLLEGE s=
a+b+c+d A circle is circumscribed about a triangle if it
Tacloban City 2 Sum of interior angles passes through the vertices of the triangle.
∠A + ∠C ∠B + ∠D The sum of interior angles θ of a polygon
θ= or θ = of n sides is:
2 2 Sum, Σθ = (n – 2) × 180°
The content of this material is one Circumcenter a r
of the intellectual properties of Given four sides a, b, c, d, and two Sum of exterior angles of the triangle
opposite angles B and D: c
Engr. Romel Tarcelo F. Verterra of The sum of exterior angles β is equal to
360°. b
Asian Development Foundation Divide the area into two triangles abc
∑β = 360° r=
College. Reproduction of this A = ½ ab sin B + ½ cd sin D
4A T
copyrighted material without
consent of the author is punishable AT = area of the triangle
by law. Circle inscribed in a triangle (Incircle)
Parallelogram Number of diagonals, D
The diagonal of a polygon is the line A circle is inscribed in a triangle if it is tangent to
Part of: B C segment joining two non-adjacent sides. the three sides of the triangle.
Plane and Solid Geometry by The number of diagonals is given by: B
d1 d2 Incenter of
RTFVerterra © October 2003 θ b n the triangle
D = (n − 3)
2 AT
A D r= c
a a
PLANE GEOMETRY Given diagonals d1 and d2 and included
angle θ:
Regular polygons s
s = ½(a + b + c)
r r
Polygons whose sides are equal are called r
PLANE AREAS A = ½ d1 × d2 × sin θ equilateral polygons. Polygons with equal
interior angles are called equiangular polygons. A C
Given two sides a and b and one angle A: b
Polygons that are both equilateral and
Triangle B
A = ab sin A equiangular are called regular polygons. The Circles escribed about a triangle
area of a regular polygon can be found by
(Excircles)
c Rhombus C considering one segment, which has the form of
a h D an isosceles triangle. A circle is escribed about a triangle if it is
d1 tangent to one side and to the prolongation of
d2 x Circumscribing
θ a circle the other two sides. A triangle has three
C A 90° escribed circles.
b x
x Inscribed
Given base b and altitude h B a A R R
θ circle
θ θ ra
A = ½ bh Given diagonals d1 and d2:
A = ½ d1 × d2 r θ θ ra
c
Given two sides a and b and included a
angle θ: x Apothem x ra
A = ½ ab sin θ Given side a and one angle A:
A = a2 sin A x b
Given three sides a, b, and c: (Hero’s AT AT AT
Formula) x = side ra = ; rc = ; rb =
Trapezoid a s−a s−c s −b
θ = angle subtended by the side from the
A= s( s − a)(s − b)(s − c ) center
R = radius of circumscribing circle Circle circumscribed about a quadrilateral
a+b+c h
s= r = radius of inscribed circle, also called the
2 a+b apothem A circle is
A= h circumscribed b
2 n = number of sides
The area under this condition can also be b about a r c
solved by finding one angle using cosine law quadrilateral if it
Cyclic Quadrilateral C θ = 360° / n passes through a
and apply the formula for two sides and
included angle. A cyclic b Area, A = ½ R2 sin θ × n = ½ x r × n the vertices of d
quadrilateral is a B c the quadrilateral.
Given three angles A, B, and C and one quadrilateral Perimeter, P = n × x
side a: whose vertices d1 n−2
lie on the Interior angle = × 180° (ab + cd)(ac + bd)(ad + bc )
a 2 sin B sin C d2 D n r=
A= circumference of a 4 A quad
2 sin A a circle. Exterior angle = 360° / n
d
The area under this condition can also be ∠A + ∠C = 180° A Circle Aquad = ( s − a)(s − b)(s − c )(s − d)
solved by finding one side using sine law and ∠B + ∠D = 180°
apply the formula for two sides and included r s = ½(a + b + c + d)
Circumference = 2π r = πD
angle. Area = ( s − a)( s − b)( s − c )( s − d) D
π 2
a+b+c+d Area, A = π r2 = D
Rectangle s= 4 Circle incribed in a quadrilateral
2 b
d A circle is
a Sector of a circle inscribed in a
Ptolemy’s theorem quadrilateral
πrθ C r
“For any cyclic quadrilateral, the product of the Arc C = r × θradians = if it is tangent
b diagonals equals the sum of the products of the 180° to the three
Area, A = ab a c
opposite sides” πr 2 θ sides of the
Perimeter, P = 2(a + b) d1 × d2 = ac + bd Area = ½ r2 θradians = r θ r quadrilateral.
360°
Diagonal, d = a 2 + b 2 Area = ½ C × r O
d
POLYGONS A quad
Square Note: 1 radian is the angle θ such that C = r. r= ; s = ½(a + b + c + d)
s
d There are two basic types of polygons, a convex Segment of a circle C
Area, A = a2 a and a concave polygon. A convex polygon is Aquad = abcd
Perimeter, P = 4a one in which no side, when extended, will pass Area = Asector – Atriangle
a inside the polygon, otherwise it called concave Area = ½ r2 θr – ½ r2 sin θ
Diagonal, d = a 2 polygon. The following figure is a convex Area = ½ r2 (θr – sin θ) r θ r
polygon.
General quadrilateral
b
C β4 θr = angle in radians
O
SOLID GEOMETRY
β3 θ4
Area = Asector + Atriangle POLYHEDRONS
B θ5 Area = ½ r2 αr + ½ r2 sin θ α = 360 - θ
c θ3 β5
θ Area = ½ r2 (αr + sin θ) r θ r A polyhedron is a closed solid whose faces are
d1
a polygons.
d2 β2 Parabolic segment
θ2 θ6
D
θ1 2
A d β1 β6 Area = bh
3 h
Given diagonals d1 and d2 and included Polygons are classified according to the number
angle θ: of sides. The following are some names of
polygons. Ellipse b
A = ½ d1 × d2 × sin θ Area = π a b PRISM
3 sides = triangle Perimeter, P
4 sides = quadrangle or quadrilateral b
a a
5 sides = pentagon a2 + b2 A prism is a polyhedron whose bases are equal
6 sides = hexagon P = 2π b polygons in parallel planes and whose sides are
7 sides = heptagon or septagon 2 parallelograms.
8 sides = octagon Prisms are classified according to their bases.
9 sides = nonagon Thus, a hexagonal prism is one whose base is a
Plane and Solid Geometry Formulas Prepared by: RTFVerterra
hexagon, and a regular hexagonal prism has a Like prisms, cylinders are classified according to ELLIPSOID
base of a regular hexagon. The axis of a prism their bases.
is the line joining the centroids of the bases. A Azone = 2πrh Z
right prism is one whose axis is perpendicular Fixed straight line Directrix 2
to the base. The height “h” of a prism is the πh
Volume = (3r − h) b
distance between the bases. 3
a a
Spherical segment c X
h of two bases
r
h Y
h Ab
As = 2πrh 4
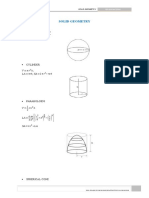
Volume = πabc
Ab πh 2 3
Volume = Ab × h Volume = (3a + 3b 2 + h2 ) b
6 Prolate spheroid
Volume = Ab × h
Right circular cylinder Spherical cone or spherical sector Prolate spheroid is formed by revolving the
ellipse about its major (X) axis. Thus from the
r figure above, c = b, then,
Rectangular parallelepiped Volume = Ab × h = π r2 h
h 4
h r Volume = πab 2
Lateral area, AL 3
d2 c AL = Base perimeter × h
r r arcsin e
d1 AL = 2 π r h As = 2πb2 + 2πab
e
b 1 2
a CONE Volume = A zone r = πr 2 h e= a2 − b2 / a
3 3
Volume = Ab × h = abc
Lateral area, AL = 2(ac + bc) A cone is the surface generated by a straight Oblate spheroid
line, the generator, passing through a fixed Spherical lune and wedge
Total surface area, AS = 2(ab + bc + ac)
point, the vertex, and moving along a fixed Prolate spheroid is formed by revolving the
Face diagonal, d1 = a2 + c 2 curve, the directrix. ellipse about its minor (Z) axis. Thus from the
figure above, c = a, then,
Space diagonal, d2 = a2 + b2 + c 2 Similar to pyramids, cones are classified r r
according to their bases. θ θ 4 2
Vertex Volume = πa b
Cube (Regular hexahedron) 3
Volume = Ab × h = a3 Ab = base area
Lateral area, AL = 4a2 h = altitude πb 2 1 + e
As = 2πa2 + ln
Total surface area Lune Wedge e 1− e
Generator
AS = 6a2 d2 h
Face diagonal a d1 A lune 4πr 2 πr 2 θ
d1 = a 2 Directrix = Alune = PARABOLOID OF REVOLUTION
a θ 360° 90°
Space diagonal
a Ab 4 3
d2 = a 3 πr
Vwedge πr 3 θ
= 3 Vwedge =
θ 360° 270° h
Truncated prism 1
Volume = Ab × h
AR = area of the right section 3 Spherical polygons
r
n = number of sides A spherical polygon is a polygon on the surface
Right circular cone of a sphere whose sides are arcs of great
r = base radius L 1 2
circles. Volume = πr h
h4 h = altitude h n = number of sides; r = radius of sphere 2
E = spherical excess ⎡ 3/2 3⎤
4πr ⎢⎛⎜ r 2 ⎞ ⎛r⎞
h1 h3 AL = 2 ⎢⎜ 4
+ h 2⎟
− ⎜⎜ ⎟⎟ ⎥
r 3h ⎟ ⎝ ⎠ ⎥⎥
2
AR a B ⎣⎢⎝ ⎠ ⎦
h2 2 2
L = slant height = r + h
r
Σh 1 1 2 A PRISMOIDAL RULE
Volume = AR Volume = Ab × h = πr h b
n 3 3
PYRAMIDS Lateral area, AL = π r L d

Frustum of a cone C Am
A pyramid is a polyhedron with a polygonal base D A1 A2
and triangular faces that meet at a common A1 = lower base area c
point called the vertex. A2 = upper base area A2
πr 2E
h = altitude Area =
Similar to prisms, pyramids are classified h 180° L/2 L/2
according to their bases. Vertex E = sum of angles – (n – 2)180°
A1 L
Ab = area of the base Spherical pyramid
L
h = altitude,
perpendicular h
Volume = ⎛⎜ A 1 + A 2 + A 1A 2 ⎞⎟ B
Volume = [A 1 + 4A m + A 2 ]
h A 6
distance from 3⎝ ⎠
the vertex to D The prismoidal rule gives precise values of
the base Frustum of right circular cone C volume for regular solid such as pyramids,
r
Ab R = lower base radius r cones, frustums of pyramids or cones, spheres,
r = upper base radius; h = altitude and prismoids.
r = radius of sphere
1 r E = spherical excess of the polygon
Volume = Ab × h E = sum of angles – (n – 2)180° SIMILAR SOLIDS
3
L πr 3E
Frustum of pyramid h Volume = Two solids are similar if any two corresponding
540° sides or planes are proportional. All spheres,
A frustum of a pyramid is the volume included cubes are similar.
between the base and a cutting plane parallel to SOLID OF REVOLUTION
the base. R
x1 x2 x1 x2
A1 = lower base area
A2 = upper base area L = slant height = h2 + (R − r ) 2 Axis of
h = altitude rotation
( )
πh 2 2 cg
Volume = R + r + Rr
3
A2 Lateral area = π (R + r) L x1 x2

h x1 x2
SPHERE R
For all similar solids:
A1 First proposition of Pappus
2 3
4 3 r The surface area generated by a surface of As1 ⎛x ⎞ V1 ⎛x ⎞
Volume = πr = ⎜⎜ 1 ⎟ and = ⎜⎜ 1 ⎟
h⎛ 3 revolution equals the product of the length of the ⎟ ⎟
Volume = ⎜ A 1 + A 2 + A 1A 2 ⎞⎟ Surface area, As = 4πr2 generating arc and the distance traveled by its
As 2 ⎝ x2 ⎠ V2 ⎝ x2 ⎠
3⎝ ⎠ centroid.
As = L × 2 π R Where As is the surface, total area, or any
CYLINDERS Spherical segment of one base Second proposition of Pappus corresponding area. The dimension x may be
the height, base diameter, diagonal, or any
A cylinder is the surface generated by a straight The volume area generated by a solid of corresponding dimension.
line intersecting and moving along a closed h revolution equals the product of the generating
plane curve, the directrix, while remaining h area and the distance traveled by its centroid.
parallel to a fixed straight line that is not on or r r
parallel to the plane of the directrix. r r Volume = A × 2 π R