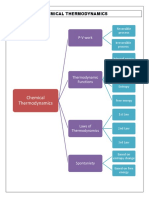
THERMODYNAMICS

PROCESSES
THERMODYNAMICS PROPERTIES THERMODYNAMICS GIBB'S FREE ENERGY
The net energy available to do useful
GIBB'S ENERGY CHANGE
& EQUILIBRIUM
• Isothermal Process work and it is a measure of ∆G° = −2.303RT log K
∆T = 0
INTENSIVE PROPERTIES EXTENSIVE PROPERTIES spontanity. ∆G° = 0 log K = 0 Equilibrium reached.
P, T, N
ZEROTH LAW OF THERMODYNAMICS Standard free energy of a reaction:
• Isochoric Process V, U, H
∆G°= Σ∆G°Products −Σ∆G°Reactants ∆G° < 0 log K > 1 Mixture contains
∆V = 0 Properties of the system Properties of the system
which are indepentent of If two bodies are in mostly products.
which depend on the amount
amount of system. A thermal equilibrium with ∆G° = ∆H° - T∆S° ∆G° > 0 log K < 1 Mixture contains
• Adiabatic Process of the system.
a third one, then they
mostly reactants.
q=0 STATE FUNCTION PATH FUNCTION
Values of such functions Values of such functions are in thermal
• Cyclic Process do not depend on the path
of the system.
depend on the path of the
system.
equilibrium with each ∆G < 0, Process is spontaneous ∆G > 0, Process is non-spontaneous
A A
∆Ucyclic = 0 other.
e.g. ∆U, ∆H, ∆S etc. e.g. W and q .
∆G = 0, Process is at equilibrium

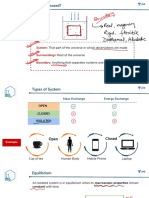
TYPES OF SYSTEM Sign of Sign of ∆ G = ∆ H − T∆ s Spontanity.

ISOTHERMAL IRREVERSIBLE ∆H ∆S
OPEN SYSTEM CLOSED SYSTEM WORK
Always
Negative Positive Spontaneous at all temp.
Wirr = -Pext ∆V Negative

Matter
ENTHALPY Positive Negative
Always Non-spontaneous at all
ISOTHERMAL REVERSIBLE Positive temperature.
Energy Energy Non-spontaneous at all
 V2  +ve @ low temp.
Wrev = -2.303nRT log   temperature.
∆H = ∆U + ∆(PV)  V1  Postive Postive
spontaneous at high
-ve @ low temp.
∆H = ∆U + ∆ngRT  P1  temperature.
ISOLATED SYSTEM Wrev = -2.303nRT log  
 P2  -ve @ low temp. spontaneous at low
Enthalpy of reaction (∆H) Negative Negative
temperature.
spontaneous at low
ADIABATIC REVERSIBLE +ve @ low temp.
Matter ∆H = Σ∆Hf(Products) - Σ∆Hf(Reactants) temperature.
nR (T -T )
Energy Wrev =
∆H = ΣB.E.Reactants - ΣΒ.ΕProducts γR 2 1
SPONTANEITY

Enthalpy of fusion (∆H°f) Enthalpy change when 1 mole of compound undergoes melting at WORK (W) It is natural direction of a process.

H 2 O(s) → H 2 O(l) constant temperature and atmospheric pressure.

HEAT (q) INTERNAL Work is a mode of energy
Enthalpy of vapourization (∆H°vap) Enthalpy change when 1 mole of compound undergoes boiling at ENERGY (U) transfer when
H 2 O() → H 2 O(g) constant temperature and atmospheric pressure. temperature difference
Exchange of energy
due to temperature Total energy within is not involved.
Enthalpy of Sublimation (∆H°sub) Enthalpy change when 1 mole of solid substance is directly converted differnece. the substance W = -Pext∆V
CO 2 (s) → CO 2 (g)
into gaseous state at a constant temperature and standard
pressure. ENTROPY
Enthalpy of Solution (∆H°sol) Enthalpy change when 1 mole of substance is dissolved in fixed FIRST LAW OF THERMODYNAMICS This is the measure of the degree of
KCl + aq → KCl (aq)
quantity of solvent. randomness or disorder of the system.
q rev
Law of conservation of energy total energy of an isolated ∆s =
T
Bond dissociation enthalpy (Β.Ε.) It is the enthalpy change to break 1 mole bonds of a particular kind. system is constant.
Cl2(g) 2Cl(g) Mathematically, ∆u= q + w ∆STotal = ∆S system
+ ∆S surroundings

Entropy changes during phase transformation

FREE EXPANSION ∆Hfusion ∆Hvap

SIGN ∆Sfusion= , ∆Svap=
Molar HEAT CAPACITY HESS' LAW CONSTANT HEAT Na+ (g) + Cl (g) T T
CONVENTION
EORN HABER CYCLE

When an ideal gas expands in vacuum ∆ H

SUMMATION then, pext = 0. ∆ sub S = subs
Amount of heat required to raise the 12∆bondH° T
Heat absorbed by the ∴ W=0
Na+(g) + 1 Cl(g) Entropy change of a reaction.
temperature of a 1 mole substance. ∆egH°
∆H1 system = +ve
A B 2
Molar heat capacity ⇒ qv = NvRT ∆ r S° = Σ s°products − Σ s°reactants
∆iH° Heat evolved by the
Specific heat capacity ⇒ qp = nCpRT 1
Na (g) + Cl(g)
+ Na+ (g) + Cl (g) -
system = -ve
SECOND LAW OF
∆H ∆H2 2 THERMODYNAMICS
MEYERS'S POISSON'S ∆subH° Work done by the THIRD LAW OF
RATIO ∆H3 system = -ve The Total entropy of the universe is always THERMODYNAMICS
FORMULA D C Na (s) + 1 Cl(g)
+ ∆LatticeH° increasing in the course of every s-
Cp 2
Cp - Cv = R =γ ∆fH°
Work done on the pontaneous or natural change. The Entropy of a perfectly crystalline
Cv ∆H = ∆H1 + ∆H2 + ∆H3
system = +ve
∆STotal > 0
substance at 0 K or absolute zero
Temperature to be zero.
NaCl(s)

anand_mani16 DR. Anand Mani https://www.anandmani.com/ https://discord.io/anandmani t.me/anandmani001