Professional Documents
Culture Documents
Functions and Graphs
Uploaded by
tawananyashaCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Functions and Graphs
Uploaded by
tawananyashaCopyright:
Available Formats
Functions and
Functions and Graphs
Graphs Cheat
Cheat Sheet
Sheet Pure Year 2
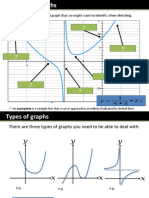
What really is a function? Combining Transformations
Before we can properly define a function, we must first understand mappings. You may also be asked to sketch transformations of modulus functions. You can apply the graph transformation techniques you learnt in
The modulus operator Chapter 4, Pure Year 1 to these problems. Recall that:
A mapping takes a set of numbers and transforms them into another set of numbers. Mappings are often represented by algebraic The modulus of any number k, denoted as |k|, is simply its non-negative value. For example, |−3| = 3 and also |3| = 3. The modulus is
equations. For example, 𝑦 = 𝑥 2 is a mapping that takes every real number and maps them to their respective squares. sometimes called the absolute value. ▪ The transformation 𝑓(𝑥) + 𝑎 is a translation of 𝑓(𝑥) by ‘a’ units in the positive y-direction.
▪ The transformation 𝑓(𝑥 + 𝑎) is a translation of 𝑓(𝑥) by ‘a’ units in the negative x-direction.
There are three different types of mappings you need to be well-acquainted with: ▪ The transformation 𝑎𝑓(𝑥) is a stretch of 𝑓(𝑥) by scale factor a in the y-direction.
Modulus functions ▪
1
The transformation 𝑓(𝑎𝑥) is a stretch of 𝑓(𝑥) by scale factor 𝑎 in the x-direction.
There are two types of modulus functions you will encounter. The first is functions of the form 𝑦 = |𝑓(𝑥)|, and the second is functions of
▪ The transformation −𝑓(𝑥) is a reflection of 𝑦 = 𝑓(𝑥) In the x-axis.
Mapping type One-to-one Many-to-one One-to-many the form 𝑦 = 𝑓(|𝑥|). Let’s discuss each of these, starting with the former.
▪ The transformation 𝑓(−𝑥) is a reflection of 𝑦 = 𝑓(𝑥) in the y-axis.
Description Each input has a unique Each input has just one There exist inputs that are 𝑦 = |𝑓(𝑥)| e.g 𝑦 = |5𝑥 − 4|
Let’s look at how we can apply the above rules to a question involving a modulus function.
output. associated output, but there are mapped to more than one With functions of this form, we can see that the modulus is placed around the entire function. This means that the function will never
some inputs that are mapped to output. output a negative number. Graphically, this means that the function will always be above (or on) the x-axis.
the same output. Example 4: Given that 𝑓(𝑥) = 2𝑠𝑖𝑛𝑥, −180° ≤ 𝑥 ≤ 180°,
𝑦 = 𝑓(|𝑥|) e.g 𝑦 = sin |𝑥| sketch the graphs of:
1
(i) |𝑓(−𝑥)|, (ii) 2𝑓(|𝑥|) + 4
Example 2
Here, the modulus is applied to the inputs of the function, rather than the outputs. This means that for any number a, we have that 𝑓(𝑎) =
𝑓(−𝑎). Graphically, this means that the function is symmetric about the y-axis.
(𝑖) ½|𝑓(−𝑥)| (𝑖𝑖) 2𝑓(|𝑥|) + 4
The above interpretations lead us onto the following algorithms for sketching modulus functions of each form:
Step Corresponding graph Step Corresponding graph
𝑦=𝑥 𝑦 = 𝑥2 − 4 𝑦 = 𝑥2 − 4 𝑦2 = 𝑥 2 We start by sketching We start by sketching
𝑦=𝑥 𝑦2 = 𝑥2 [A] 𝑦 = |𝑓(𝑥)|
𝑓(𝑥) 𝑓(𝑥)
1) Start by sketching the graph 𝑦 = 𝑓(𝑥).
2) Take the section of the graph below the x-axis and reflect it in the x-axis.
• Functions are mappings that are one-to-one or many-to-one. One-to-many mappings are not functions!
[B] 𝑦 = 𝑓(|𝑥|) Now sketching 𝑓(−𝑥) Now we sketch 𝑓(|𝑥|) by
(reflect the graph in the reflecting the graph of
Function notation 1) Start by sketching the function for 𝑥 ≥ 0. y-axis). 𝑓(𝑥) for 𝑥 ≥ 0 in the
You need to understand what is meant by the domain and range of a function: 2) Reflect this in the y-axis. y-axis.
▪ The domain of a function is the set of all possible inputs (i.e. the set of x-values the function takes)
▪ The range of a function is the set of all possible outputs (i.e. the set of y-values the function takes) Example 2: Given that 𝑓(𝑥) = 𝑥 2 − 7𝑥 − 8, sketch: (𝑖) |𝑓(𝑥)|, (𝑖𝑖) 𝑓(|𝑥|) Applying the modulus Stretching the graph by a
function now to sketch scale factor of 2 in the
There are two main types of notation you will see for denoting functions: | 𝑓(𝑥)|. The portion of y-direction to achieve
(𝑖) |𝑓(𝑥)| (𝑖𝑖) 𝑓(|𝑥|)
the graph below the x- 2 𝑓(|𝑥|).
▪ 𝑓(𝑥) = √𝑥, {𝒙 ∈ ℝ, 𝒙 ≥ 𝟎} axis is reflected in the x-
Step Corresponding graph Step Corresponding graph
▪ 𝑓: 𝑥 ⟼ √𝑥, {𝒙 ∈ ℝ, 𝒙 ≥ 𝟎} axis.
We start by sketching Start by sketching Stretching our graph by a Finally, we translate our
These notations are equivalent for one-to-one or many-to-one functions. The “ ⟼ " symbol means that each element in the 𝑦 = 𝑥 2 − 7𝑥 − 8. 𝑦 = 𝑥 2 − 7𝑥 − 8 for 𝑥 ≥ 0. scale factor of ½ to attain graph up by 4 units giving
domain is mapped to just one element in the range. The bold text represents the domain of the function. the graph of ½|𝑓(−𝑥)| us the graph of
2𝑓(|𝑥|) + 4.
Composition of functions
We can combine two or more functions to make a new function. This new function is called a composite function.
Let’s take two functions, 𝑔(𝑥) and 𝑓(𝑥). If we wish to combine them, there are two ways we can do this: Next, we reflect the Now reflect the graph in
portion of the graph below the y-axis.
▪ 𝑓𝑔(𝑥) we interpret this as applying 𝑔(𝑥) first, then 𝑓(𝑥). the x-axis in the x-axis.
Solving modulus equations
▪ 𝑔𝑓(𝑥) we interpret this as applying 𝑓(𝑥) first, then 𝑔(𝑥).
You can also be expected to be able to solve equations involving modulus and non-modulus functions. It is best to first sketch the functions
within your equation so that you can figure out graphically where the solutions are located, and then use your knowledge of modulus functions
It is important to realise that 𝑔𝑓(𝑥) ≠ 𝑓𝑔(𝑥) in general.
to completely solve the equation.
When composing functions, it is helpful to interpret 𝑓𝑔(𝑥) as 𝑓[𝑔(𝑥)]. This means that we must replace the inputs of 𝑓(𝑥) with
𝑔(𝑥), to get 𝑓𝑔(𝑥) . Example 5: Given that 𝑎 and 𝑏 are constants, and that 0 < 𝑎 < 𝑏,
Below is an example of how we do this in practice. 1
Inverse functions Solve, for 𝑥, the equation |2𝑥 + 𝑎| − 𝑏 = 𝑥
3
−1
The inverse of a function 𝑓(𝑥), denoted by 𝑓 (𝑥), is another function that “reverses” 𝑓(𝑥). It maps elements in the range of
1 𝑦 = |2𝑥 + 𝑎| − 𝑏
𝑓(𝑥) back into the domain of 𝑓(𝑥). This is why inverse functions are only defined for one-to-one functions. We start by sketching |2𝑥 + 𝑎| − 𝑏 and 𝑦 = 3 𝑥 on the same axes. Use your
Example 1: Given that 𝑓(𝑥) = 3𝑥 − 2 and 𝑔(𝑥) = 𝑥 2 + 4𝑥 − 2, find an expression for:
(i) 𝑓𝑔(𝑥) knowledge of combinations of transformations and modulus functions to do
Here are four key points regarding inverse functions that follow from our above definition: this. 1
(ii) 𝑔𝑓(𝑥) 𝑦= 𝑥
3
▪ An inverse function is simply the original function reflected in the line 𝑦 = 𝑥. We look at our sketch and identify the points
1
− (𝑎 + 𝑏)
[1]
(i) 𝑓𝑔(𝑥) is found by replacing all the 𝑥 terms in 𝑓𝑔(𝑥) = 𝑓[𝑔(𝑥)] = 𝑓(𝑥 2 + 4𝑥 − 2) 2
▪ For any function 𝑓(𝑥) and its inverse 𝑓 −1 (𝑥), we have that 𝑓𝑓 −1(𝑥) = 𝑓 −1𝑓(𝑥) = 𝑥. of intersection (labelled [1] and [2]). These are the points 1
𝑓(𝑥) with 𝑥 2 + 4𝑥 − 2 (𝑏 − 𝑎)
▪ The domain of 𝑓(𝑥) is the range of 𝑓 −1(𝑥). we want to find. 2
[1]
Doing so: 𝑓(𝑥 2 + 4𝑥 − 2) = 3(𝑥 2 + 4𝑥 − 2) − 2 [2]
▪ The domain of 𝑓 −1(𝑥) is the range of 𝑓(𝑥).
Simplifying gives: 𝑓(𝑥 2 + 4𝑥 − 2) = 3𝑥 2 + 12𝑥 − 6 𝑎 −𝑏
The final answer is: so 𝑓𝑔(𝑥 ) = 3𝑥 2 + 12𝑥 − 6 You need to know how to find the inverse of a given function, 𝑦 = 𝑓(𝑥). The procedure can be summarised in 3 steps:
(ii) 𝑔𝑓(𝑥) is found by replacing all the 𝑥 terms in 𝑔𝑓(𝑥) = 𝑔[𝑓(𝑥)] = 𝑔(3𝑥 − 2)
Point [1] is an intersection of the non-reflected portion 1
𝑔(𝑥) with 3𝑥 − 2 [1] Interchange the 𝑥 and 𝑦 variables in your function. 1 2𝑥 − 𝑥 = 𝑏 − 𝑎
of |2𝑥 + 𝑎| − 𝑏 with 𝑥. Therefore, if we wish to find this 3
Doing so: 𝑔(3𝑥 − 2) = (3𝑥 − 2)2 + 4(3𝑥 − 2) − 2 3 5
1
Simplifying gives: 𝑔(3𝑥 − 2) = 9𝑥 2 − 12𝑥 + 4 + 12𝑥 − 8 − 2 = 9𝑥 2 − 4 [2] Rearrange your equation to make 𝑦 the subject again. point, we need to solve 2𝑥 + 𝑎 − 𝑏 = 3 𝑥. ∴ 𝑥 =𝑏−𝑎
3
The final answer is: 𝑠𝑜 𝑔𝑓(𝑥) = 9𝑥 2 − 4 𝟑
so 𝒙 = 𝟓 (𝒃 − 𝒂) [1]
[3] This new function you have found is the inverse.
Point [2] is an intersection of the reflected portion of |2𝑥 + 𝑎| − 𝑏 1
1 −2𝑥 − 𝑎 − 𝑏 = 𝑥
with 3 𝑥. Therefore, to find [2], we must solve the equation −(2𝑥 + 𝑎) − 3
Example 3: Find the inverse of the function 𝑓(𝑥) = 𝑥 3 − 8 {𝑥 ∈ ℝ, 𝑥 ≥ 2}, stating its range. 7 𝟑
It is clear from this example that 𝑔𝑓(𝑥) ≠ 𝑓𝑔(𝑥). 𝑏 = 3𝑥
1 − 𝑥 = 𝑎 + 𝑏 ∴ 𝒙 = − (𝒂 + 𝒃) [2]
3 𝟕
[1] We have 𝑦 = 𝑥 3 − 8, so interchanging 𝑥 and 𝑦: 𝑥 = 𝑦3 − 8
[2] Rearranging to make y the subject 3
𝑦 = √𝑥 + 8
[3] This function is our inverse. 3
𝑓 −1(𝑥) = √𝑥 + 8
The range will be the same as the domain of the original function Range: 𝑦 ≥ 2 This process can be applied to any question where you need to solve an equation involving modulus functions. It is crucial you are able to sketch
the graphs correctly. If you have a graphical calculator then you should always use it to check that your sketch is correct.
https://bit.ly/pmt-cc
https://bit.ly/pmt-edu https://bit.ly/pmt-cc
You might also like
- Ch.2 Functions and GraphsDocument1 pageCh.2 Functions and GraphshamzahNo ratings yet
- Functions GuideDocument3 pagesFunctions GuideTaehyeon KimNo ratings yet
- Chapter 3 - Laplace TransformDocument57 pagesChapter 3 - Laplace TransformBukhari ManshoorNo ratings yet
- Syllabus OutlineDocument2 pagesSyllabus OutlineElena GilbertNo ratings yet
- FunctionsDocument29 pagesFunctionsmartinajoan1No ratings yet
- LC of Error FunctionDocument7 pagesLC of Error Function孟栋梁No ratings yet
- Linear Graphs:: Functions & Graphs My Maths MentorDocument9 pagesLinear Graphs:: Functions & Graphs My Maths MentorDâwood MehmoodNo ratings yet
- Summary Sheet: Functions: Sketching Modulus GraphsDocument3 pagesSummary Sheet: Functions: Sketching Modulus GraphsRaunak PrasadNo ratings yet
- Lecture09 CE72.12Isoparametric FormulationDocument14 pagesLecture09 CE72.12Isoparametric FormulationRahul KasaudhanNo ratings yet
- 8 Vertical TransformationsDocument4 pages8 Vertical TransformationsLaila SolimanNo ratings yet
- Inverse FunctionsDocument6 pagesInverse FunctionsNareema HendricksNo ratings yet
- Maintenance Engineering 3Document14 pagesMaintenance Engineering 3Suienish SultangazinNo ratings yet
- P2 Chp2 FunctionsAndGraphsDocument44 pagesP2 Chp2 FunctionsAndGraphsNasim SalimNo ratings yet
- Lecture 2Document67 pagesLecture 2Maisam ElkhalafNo ratings yet
- Transformations: Chapter 2 (Part 2)Document42 pagesTransformations: Chapter 2 (Part 2)Megan JunnilaNo ratings yet
- Kami Export - Appc - 1.1 - PacketDocument6 pagesKami Export - Appc - 1.1 - PacketeenamorataNo ratings yet
- Review Notes 1: Introduction to Functions (RN1Document16 pagesReview Notes 1: Introduction to Functions (RN1kopii utoyyNo ratings yet
- Graph Transformations 1Document14 pagesGraph Transformations 1Ibrahim AbdulaliNo ratings yet
- Play With GraphsDocument189 pagesPlay With GraphsRidwanullah shaikNo ratings yet
- 1 Q1 General MathematicsDocument80 pages1 Q1 General Mathematicsangelotactay06No ratings yet
- Target: Learning Guide ModuleDocument7 pagesTarget: Learning Guide ModuleI need sleepNo ratings yet
- Logarithmic PDFDocument19 pagesLogarithmic PDFMoguri PeachNo ratings yet
- PPT 1 Ex 2A - The Exponential FunctionDocument18 pagesPPT 1 Ex 2A - The Exponential FunctionRalph Rezin MooreNo ratings yet
- Linear RegressionDocument8 pagesLinear RegressionParthraj SolankiNo ratings yet
- Math 11 CORE Gen Math Q1 Week 8Document28 pagesMath 11 CORE Gen Math Q1 Week 8MeYo SanNo ratings yet
- Week 7 - Lecture NotesDocument18 pagesWeek 7 - Lecture Notesnatalievns1999No ratings yet
- 1 A 2 AfcDocument8 pages1 A 2 AfcYazan ZamelNo ratings yet
- Laplace Transforms for Solving Differential EquationsDocument31 pagesLaplace Transforms for Solving Differential EquationsJohn vincent estilles mercadoNo ratings yet
- Chapter 18 - ParabolaDocument12 pagesChapter 18 - ParabolaGicelNo ratings yet
- Module 2, Quadratic Functions & Parabolas Assignment: Standard Form Vertex FormDocument3 pagesModule 2, Quadratic Functions & Parabolas Assignment: Standard Form Vertex Formghanatia07No ratings yet
- 06 Range and FunctionDocument43 pages06 Range and FunctionBapiki CadiakNo ratings yet
- C3 Chp5 TransformingGraphsDocument19 pagesC3 Chp5 TransformingGraphsAdil HafeezNo ratings yet
- Pertemuan IV - Graphic of Function and Algebra (Autosaved)Document16 pagesPertemuan IV - Graphic of Function and Algebra (Autosaved)Devi AgustinaNo ratings yet
- Robot Arm KINEMATICs and DynamicsDocument27 pagesRobot Arm KINEMATICs and DynamicsTirth VyasNo ratings yet
- QA Basic Calculus Quarter 3 Week 6 FinalDocument7 pagesQA Basic Calculus Quarter 3 Week 6 Finalelyzaventura8No ratings yet
- Z TransformDocument37 pagesZ Transformعلي كامل الاسديNo ratings yet
- MCR 3U Characteristics of FunctionsDocument8 pagesMCR 3U Characteristics of FunctionslucasNo ratings yet
- Point GroupDocument16 pagesPoint GroupBEA FRANCINE DELOS SANTOSNo ratings yet
- Play With Graphs QXDDocument190 pagesPlay With Graphs QXDJaman Ahmed UdoyNo ratings yet
- Graphs and TransformationsDocument1 pageGraphs and TransformationstawananyashaNo ratings yet
- Lecture FunctionsDocument28 pagesLecture FunctionsShifaNo ratings yet
- SLG 7.1.1 Functions That Have Inverses 1Document8 pagesSLG 7.1.1 Functions That Have Inverses 1Faye AbianNo ratings yet
- End of Year 1 Exam Possible TopicsDocument7 pagesEnd of Year 1 Exam Possible TopicsLinh (Viso) DoNo ratings yet
- DfafDocument27 pagesDfafKoby TosocNo ratings yet
- Math Concepts Reference Guide PDFDocument7 pagesMath Concepts Reference Guide PDFAUSTRANo ratings yet
- 1 MTN-4Document8 pages1 MTN-4Mon Henry EgnisabanNo ratings yet
- Mathematical Tools: Introduction To FunctionsDocument71 pagesMathematical Tools: Introduction To FunctionsKripa mariam JosephNo ratings yet
- Chapter One: Sulaimani Polytechnic University/ Technical College of Engineering Mechanical Engineering DepartmentDocument28 pagesChapter One: Sulaimani Polytechnic University/ Technical College of Engineering Mechanical Engineering DepartmentAll TutorialNo ratings yet
- v2 - SLG M2 9.2.1 - Graph of An Absolute Value Function PDFDocument12 pagesv2 - SLG M2 9.2.1 - Graph of An Absolute Value Function PDFLiericka May SupasNo ratings yet
- Skills in Mathematics Play With Graphs For JEE Main and Advanced 2022Document189 pagesSkills in Mathematics Play With Graphs For JEE Main and Advanced 2022Harshil Nagwani67% (3)
- Composite and Inverse Functions: Mrs. Aldous, Mr. Beetz & Mr. Thauvette IB DP SL MathematicsDocument12 pagesComposite and Inverse Functions: Mrs. Aldous, Mr. Beetz & Mr. Thauvette IB DP SL MathematicsAnnanya GuhaNo ratings yet
- Intergal CalculusDocument20 pagesIntergal CalculusElizabeth ErwanNo ratings yet
- College Algebra v3 2 Ch05 Powerpoint Lecture Notes-FW BADocument33 pagesCollege Algebra v3 2 Ch05 Powerpoint Lecture Notes-FW BAzanyar RaufNo ratings yet
- MAT-142 - PPT - Function-Monsoon 2021 - StudentDocument38 pagesMAT-142 - PPT - Function-Monsoon 2021 - StudentHappy PanjwaniNo ratings yet
- Lecture 4 (Laplace Transform Review)Document19 pagesLecture 4 (Laplace Transform Review)muhammad hamzaNo ratings yet
- Week 7 Derivative of Exponential and Logarithmic FunctionsDocument6 pagesWeek 7 Derivative of Exponential and Logarithmic FunctionsTirzah GinagaNo ratings yet
- Math2200ch7 4notes-WorkingsDocument6 pagesMath2200ch7 4notes-WorkingsDaRealTruthNo ratings yet
- Reciprocal Functions: Lesson 6Document4 pagesReciprocal Functions: Lesson 6luluhbelle cruzNo ratings yet
- Radian SDocument1 pageRadian StawananyashaNo ratings yet
- Sequences and SeriesDocument1 pageSequences and SeriestawananyashaNo ratings yet
- Quadratics Cheat Sheet Edexcel Pure Year 1: Function 3 + 2 11Document1 pageQuadratics Cheat Sheet Edexcel Pure Year 1: Function 3 + 2 11online classNo ratings yet
- Graphs and TransformationsDocument1 pageGraphs and TransformationstawananyashaNo ratings yet
- Caie As Level Geography 9696 Case Studies v1Document18 pagesCaie As Level Geography 9696 Case Studies v1BrizzyNo ratings yet
- Cambridge Assessment International EducationDocument16 pagesCambridge Assessment International EducationKiarash SoleimaniNo ratings yet
- Global Perspectives & Research-2022-SyllabusDocument44 pagesGlobal Perspectives & Research-2022-SyllabustawananyashaNo ratings yet
- Deign & Technology 2023 SyllabusDocument34 pagesDeign & Technology 2023 SyllabustawananyashaNo ratings yet
- MATHEMATICAL ECONOMICSDocument54 pagesMATHEMATICAL ECONOMICSCities Normah0% (1)
- Class 9 - IMO 2Document5 pagesClass 9 - IMO 2VaidayNo ratings yet
- Excel - Functions & FormulasDocument9 pagesExcel - Functions & FormulasPrabodh VaidyaNo ratings yet
- Trading Systems and MethodsDocument5 pagesTrading Systems and Methodssanjay patidarNo ratings yet
- A NGLEDocument8 pagesA NGLEYashita JainNo ratings yet
- Finding The Domain and Range of A FunctionDocument21 pagesFinding The Domain and Range of A FunctionNoreen Patayan100% (1)
- Predictor-Corrector MethodDocument3 pagesPredictor-Corrector Methodletter_ashish4444No ratings yet
- Equivalence WFFDocument7 pagesEquivalence WFFSambasivam RamasubramanianNo ratings yet
- Optimum Tuning UPFC Via ACODocument8 pagesOptimum Tuning UPFC Via ACORuzaini GcornNo ratings yet
- Learn math through six stages of playing games and abstracting common rulesDocument2 pagesLearn math through six stages of playing games and abstracting common rulesChin Boon KingNo ratings yet
- Sullivan, Clarke & Clarke (2013, Ch.3)Document9 pagesSullivan, Clarke & Clarke (2013, Ch.3)Syb croNo ratings yet
- The Quadratic Formula and The Discriminant: You Should LearnDocument8 pagesThe Quadratic Formula and The Discriminant: You Should Learnfalcon724No ratings yet
- Chapter 4 - Exponentional and Logarithmic Functions - Math in Focus Year 12Document33 pagesChapter 4 - Exponentional and Logarithmic Functions - Math in Focus Year 12Riche LanNo ratings yet
- Paper of Linear ProgrammingDocument10 pagesPaper of Linear ProgrammingkhalishahNo ratings yet
- Data Management ModuleDocument35 pagesData Management ModuleJoksian Trapela100% (1)
- Mathematical&Usaefuldiscrete ExamplesDocument2 pagesMathematical&Usaefuldiscrete ExamplesJenalyn QuemadaNo ratings yet
- Fe 3163Document10 pagesFe 3163nor fazlinaNo ratings yet
- EC8553 Discrete Time Signal Processing MCQ PadeepzDocument17 pagesEC8553 Discrete Time Signal Processing MCQ PadeepzNivethaNo ratings yet
- SCF Convergence and Chaos TheoryDocument4 pagesSCF Convergence and Chaos Theoryadu666No ratings yet
- Lesson Plan-Law of SinesDocument6 pagesLesson Plan-Law of Sinesapi-284750579100% (8)
- A Method For Cycle Time Estimation of Semiconductor Manufacturing Toolsets With CorrelationsDocument11 pagesA Method For Cycle Time Estimation of Semiconductor Manufacturing Toolsets With CorrelationsDeepak JainNo ratings yet
- Homework8 AnsDocument3 pagesHomework8 AnsAshok ThiruvengadamNo ratings yet
- Practice Questions: Cambridge IGCSE Mathematics 0580Document37 pagesPractice Questions: Cambridge IGCSE Mathematics 0580Hayaa KhanNo ratings yet
- Topic 4 (Money) - Y4 09Document16 pagesTopic 4 (Money) - Y4 09Noorizan Mohd Esa0% (1)
- AMC Practice Problems Solutions Set1 MPRDocument3 pagesAMC Practice Problems Solutions Set1 MPRPaula Ty-RelucioNo ratings yet
- c4 VectorsDocument42 pagesc4 VectorsrendhelNo ratings yet
- Relative-Motion Analysis of Two Particles Using Translating AxesDocument18 pagesRelative-Motion Analysis of Two Particles Using Translating AxesAtef NazNo ratings yet
- HW 02Document12 pagesHW 02Shubhankar Gautam100% (1)
- Genetic Algorithm Solution of The TSP Avoiding Special Crossover and MutationDocument6 pagesGenetic Algorithm Solution of The TSP Avoiding Special Crossover and MutationMuhammad FadzreenNo ratings yet
- 6th Grade Math Worksheets PDF, 6th Grade Math TestDocument45 pages6th Grade Math Worksheets PDF, 6th Grade Math TestBenjamin Lawrence100% (1)